この記事はOpen and Reproducible Science Advent Calendar 2019の17日目の記事です。
これまでの記事では主に再現性の問題が取り扱われています。
本稿では臨床疫学領域で近年注目されている中断時系列分析 (interrupted time series analysis: ITSA) の方法論的な問題点と、それによって生じる解釈可能性への影響について述べます。アドカレの趣旨からは若干ずれるかもしれませんが、お付き合い頂けますと幸いです。
中断時系列分析はある介入またはイベントが時系列で測定されるアウトカムへおよぼす影響を評価する統計学的な手法のひとつです。介入前のトレンドが介入によって中断されているかを、反事実と比較することで評価します。RCTが適用できない状況での因果推論の手法として有効であり、制度や政策の影響の評価にも使用しやすい、とても便利な手法です。詳しくは中断時系列分析については宜保さんのスライドがわかりやすいのでご覧下さい。
中断時系列デザインは、より厳密には中断時系列デザインに回帰分断デザイン (regression discontinuity design) を適応したものといえます。回帰分断デザインの他にも、ARIMAXモデル () や外生変数を持つ状態空間モデル (state-space model) などを中断時系列デザインに用いることができます。
Y = β0 + β1X + β2t + β3Xt …… (1)
線型モデルを用いた中断時系列分析は (1) 式のように立式されます。第1項のβ0は介入開始前の水準を表します。第2項Xは介入の有無で、通常はダミー化され、介入前を0、介入後を1とコードします。その係数β1は介入に伴う水準の変化を意味します。第3項のtは時系列で、通常は観察開始点を1とし、1観察につき1ずつ増加します。第4項のXtは時系列と水準の交互作用項で、その係数β3は介入に伴う傾きの変化を意味します。第4項の後に周期性等を補正するための項を置くこともありますが、本稿では省いています。換言すると、中断時系列デザインは、時系列データへの介入の影響を、水準の変化と傾きの変化に分けて同時に評価しています。水準の変化と傾きの変化を同時に評価できることは、ARIMAXモデルや状態空間モデルにはない中断時系列分析の特徴です (ARIMAXや状態空間モデルで水準と傾きの変化を同時に扱う方法があれば教えてください)。
ところで、線型モデルを用いる際に注意すべき点として多重共線性の問題があります。多重共線性とは、複数の独立変数間に強い相関がみられる場合に、それらの独立変数の効果推定値の分散が過大に推定され、結果として効果推定値が過小評価されることです。多重共線性が発生しているかどうかはvariance inflation factor (VIF) を用いて評価します。慣習的にはVIFが5または10を超えている場合に多重共線性の発生を疑い、相関の高い独立変数のうち一方を解析から除外するのなどの措置を行います。多重共線性を発生させうる代表的な統計学的な操作のひとつが交互作用項の投入です。
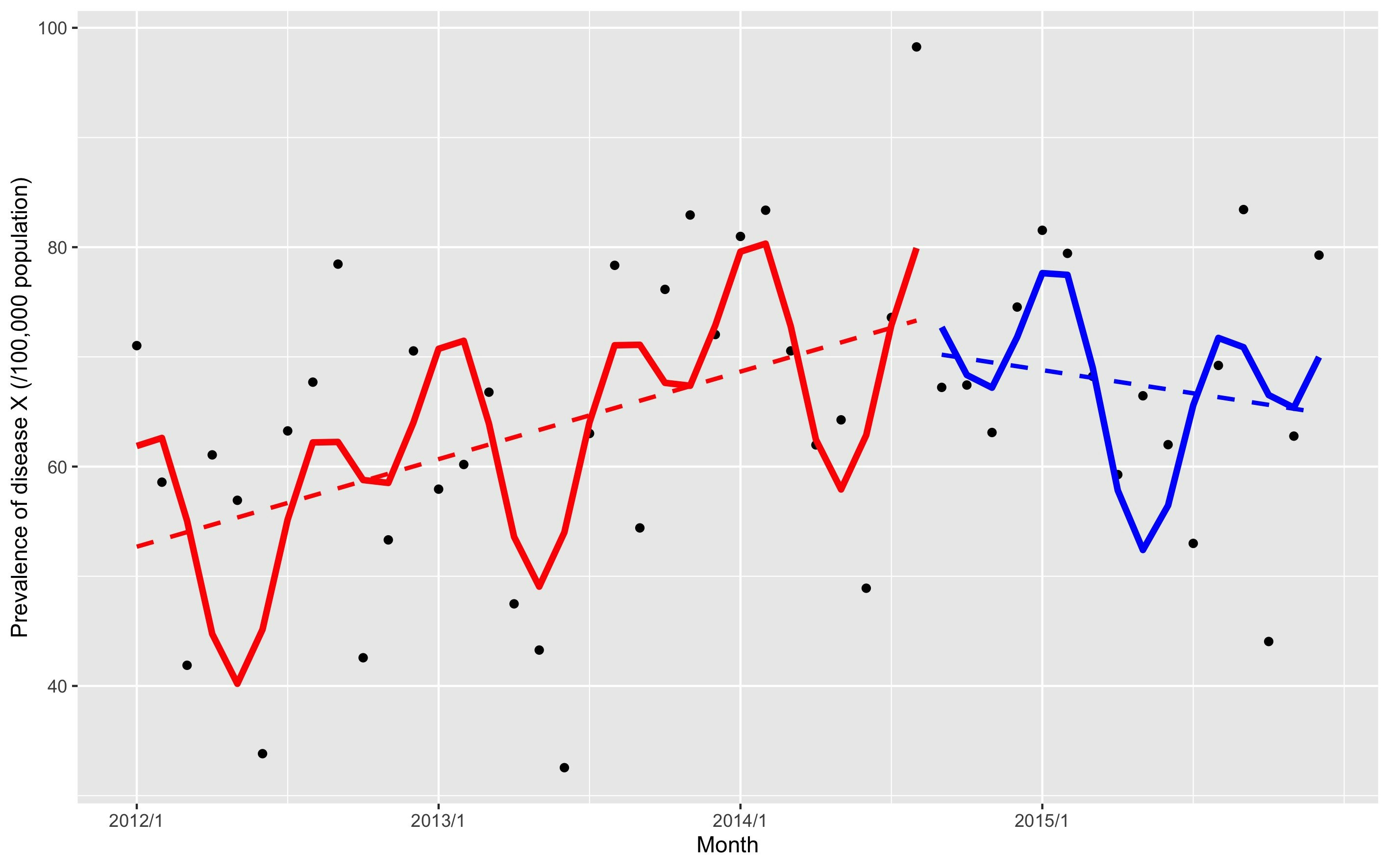
中断時系列デザインや回帰分断デザインは、傾きの変化の評価のために交互作用項を投入することから、多重共線性が生じるリスクの高い手法です。下図はダミーデータをもとにしたもので、某市でのとある疾患Yの人口10万人あたりの発生率を施策Xの実施前後で中断時系列分析を用いて比較したものです。疾患Yの発生率は増加傾向にありましたが、施策Xの実施後に減少傾向へと転じていることが読み取れます。しかし、施策Xの水準への影響 (β = 54.2, 95%CI = [-39.55, 147.90])、傾きへの影響 (β = -0.9, 95%CI = [-2.14, 0.36]) は共に有意ではなく、とくに水準への影響の推定値が異常です。VIFはそれぞれ197.88, 209.49と10を大きく超えています。この結果をどのように解釈すれば良いでしょうか。多重共線性が生じていることから統計解析の結果をそのまま採用することは慎むべきです。その一方で、特に傾き変化が有意でないのは直観に反するように感じます。多重共線性への対処として交互作用項を除去することも考慮しますが、傾きの変化を評価しないものどうかと思い……正直、解釈にも手続き的にも困ります。
ここまで、中断時系列デザインが解析の構造的に多重共線性が生じやすいことを述べてきました。しかしながら、中断時系列デザインの多重共線性問題について、医療や公衆衛生の領域ではどうも認識されていないようです。回帰分断デザインの多重共線性リスクは10年以上前に指摘されていますが、中断時系列デザインでの多重共線性のリスクは筆者の調べた限りこれまでに指摘されていません。2015年には薬剤利用研究での報告の特徴と推奨事項 が、2019年7月には医療領域での報告の特徴 が、それぞれ報告されました。しかし、いずれの論文でも多重共線性の評価は項目として含まれていません。筆者はこれまでに数十の中断時系列分析を用いた研究に目を通してきましたが、その多く変数選択の後に交互作用項を含まないモデルが選択されおり、VIFを報告している研究に出会ったことがありません。今後しばらくはこのような研究が増え続けると予想しています。
それでは、中断時系列分析の多重共線性リスクにどう対処すれば良いのでしょうか。
研究者として中断時系列分析を行う際は、棄却されたモデルに対しても多重共線性のチェックを行い、その全てを論文内で報告するべきだと筆者は考えます。傾きの変化と水準の変化を同時に評価する必要がないのであれば、状態空間モデルやARIMAXを用いることを考慮すると良いでしょう。中断時系列分析を用いた研究を読む際は、採用しなかったモデルも含めて交互作用項を投入しているか、VIF等を用いて多重共線性を評価しているかの2点を評価すると良いと思います。
なお本稿は筆者の私見を含むこと、現時点で統計学/生物統計学領域でのコンセンサスでないことはご承知おき下さい。誤り等があればご指摘頂けますと幸いです。