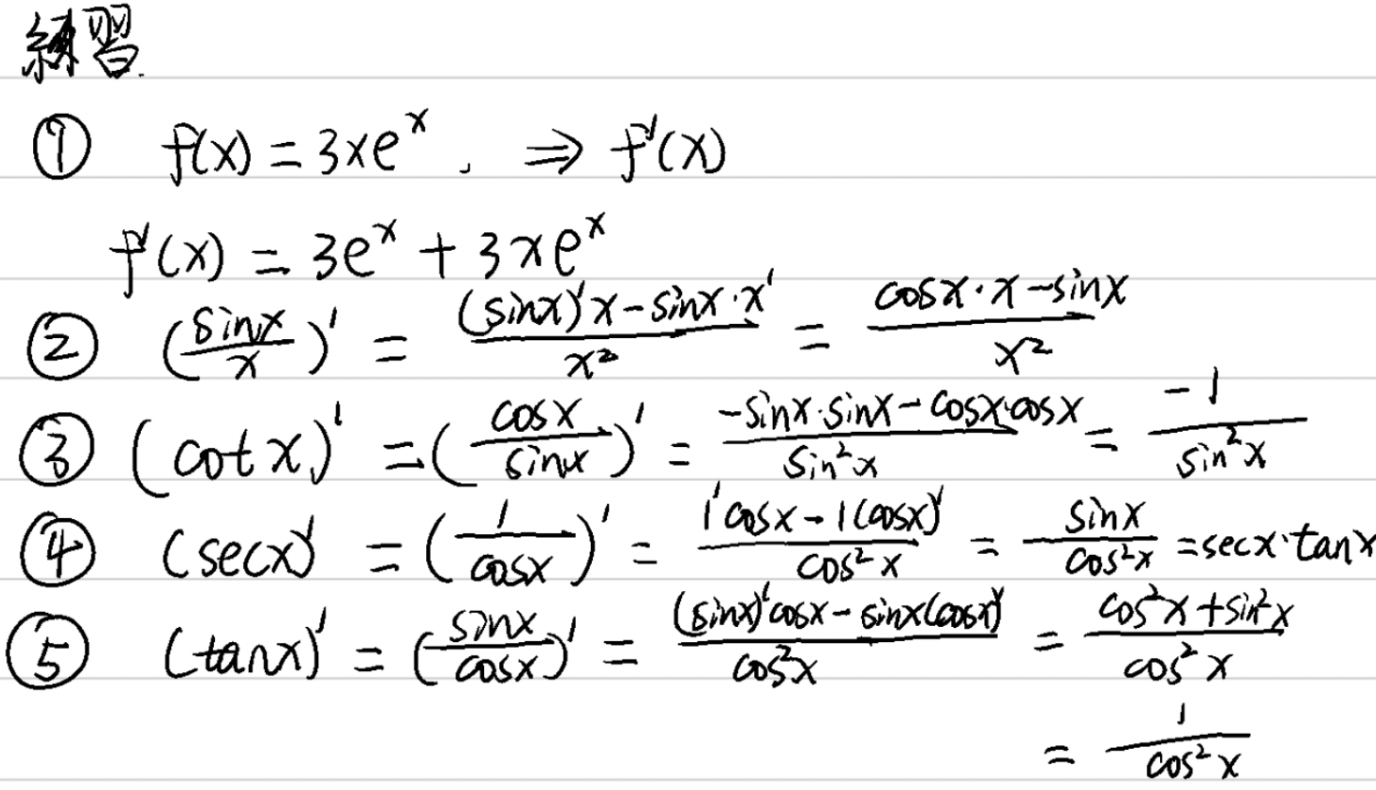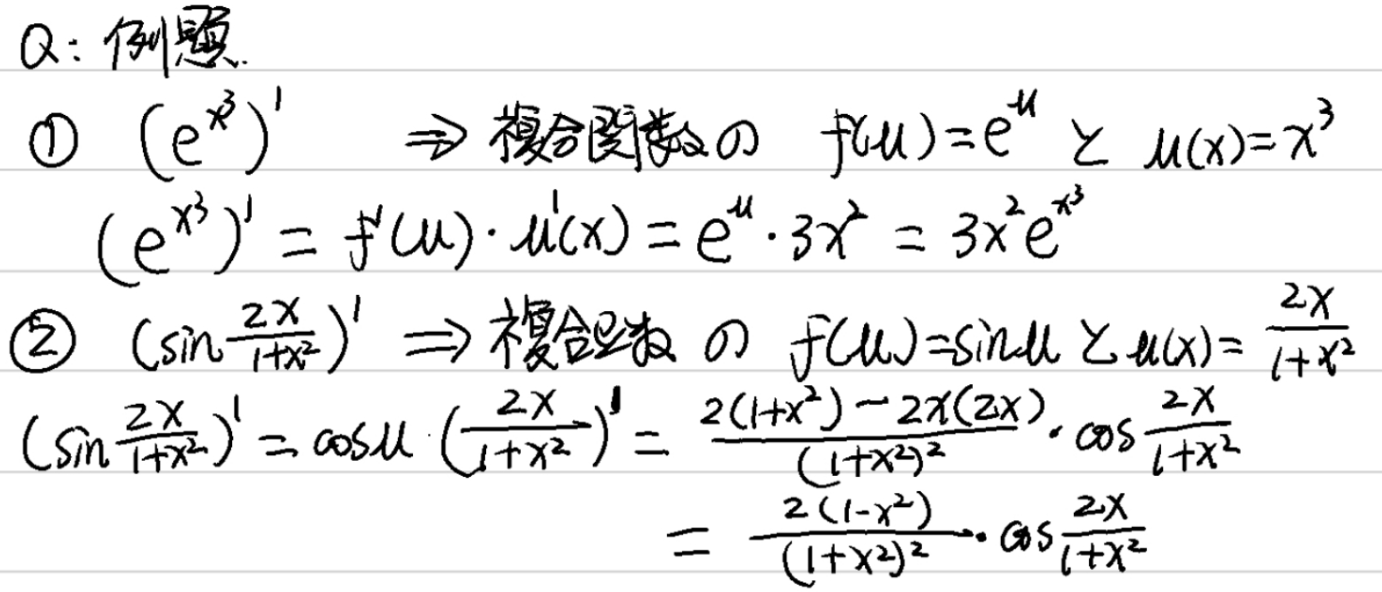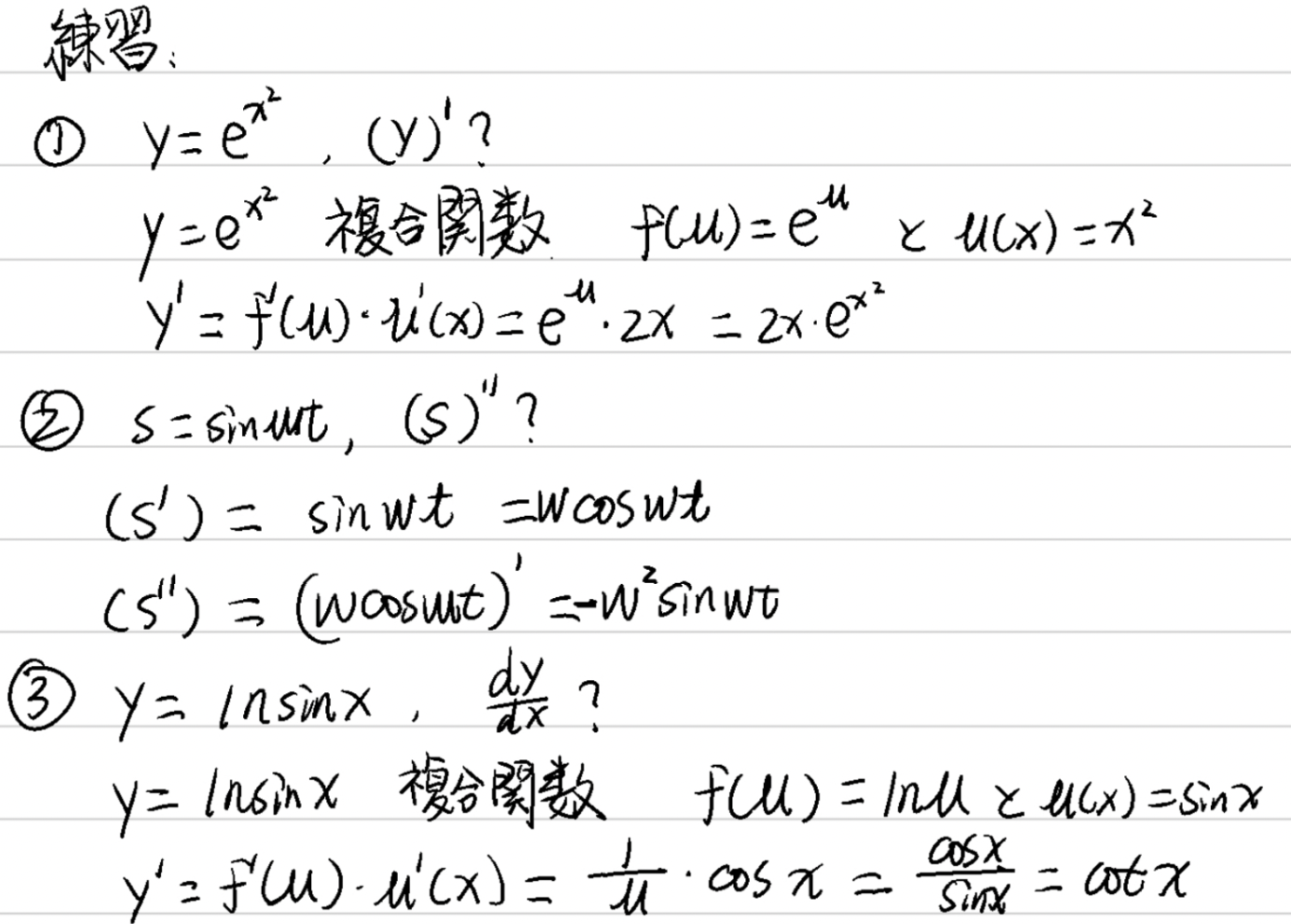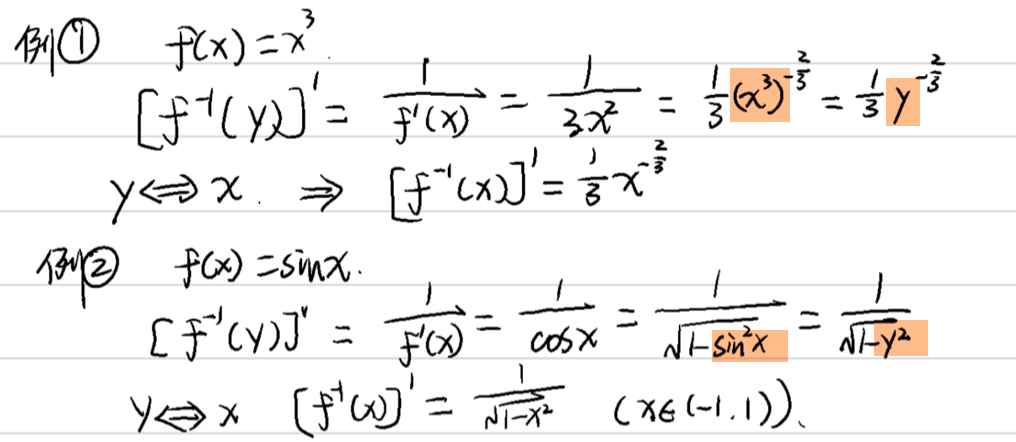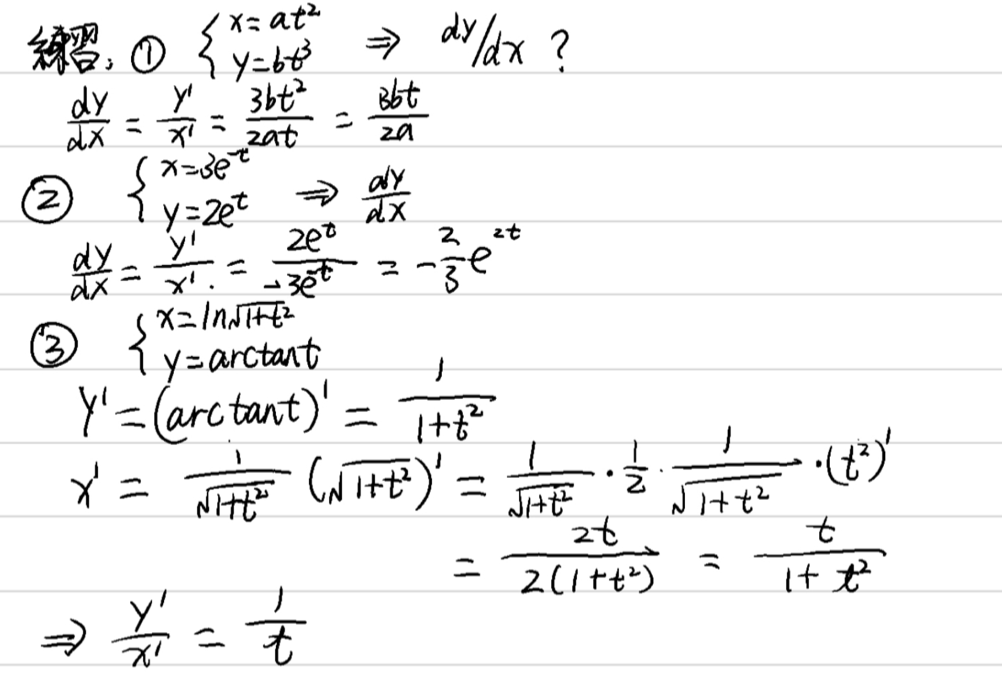本記事は数学講座3.1微分と線形近似を勉強して投稿したメモです。詳細は元の素晴らしい講座のページをチェックしてください。
 纏め
纏め
微分と導数の定義
\begin{aligned}
\text{微分(局所的な曲線を近似できる直線)}:&\qquad \mathrm{d}y=f'(x_0)\mathrm{d}x\implies f'(x_0)=\frac{\mathrm{d}y}{\mathrm{d}x}\\
\text{導数(微分の勾配)}:&\qquad f'(x_0)=\left.\frac{\mathrm{d}y}{\mathrm{d}x}\right|_{x=x_0}=\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}
\end{aligned}
一般的な導関数
\begin{array}{c|c|c}
\hline
\\
\quad\text{常数函数}\quad &\quad f(x)=C,C\in\mathbb{R} & f'(x)=0\\
\\
\hline
\\
\quad\text{幂函数}\quad &\quad f(x)=x^\alpha,\alpha\in\mathbb{R} & f'(x)=\alpha x^{\alpha-1}\\
\\
\hline
\\
\quad\quad &\quad f(x)=\sin x & f'(x)=\cos x\\
\quad\text{三角函数}\quad &\quad f(x)=\cos x & f'(x)=-\sin x\\
\quad\quad &\quad f(x)=\tan x & f'(x)=\sec^2 x\\
\quad\quad &\quad f(x)=\cot x & f'(x)=-\csc^2 x\\
\\
\hline
\\
\quad\quad &\quad f(x)=\arcsin x & f'(x)=\frac{1}{\sqrt{1-x^2}}\\
\quad\text{反三角函数}\quad &\quad f(x)=\arccos x & f'(x)=-\frac{1}{\sqrt{1-x^2}}\\
\quad\quad &\quad f(x)=\arctan x & f'(x)=\frac{1}{1+x^2}\\
\quad\quad &\quad f(x)=\text{arccot} x & f'(x)=-\frac{1}{1+x^2}\\
\\
\hline
\\
\quad\quad &\quad f(x)=a^x,a > 0, a\ne 1& f'(x)=a^x\ln a\\
\quad\text{指数函数}\quad &\quad f(x)=e^x & f'(x)=e^x\\
\\
\hline
\\
\quad\quad &\quad f(x)=\log_a x,a > 0, a\ne 1& f'(x)=\frac{1}{x\ln a}\\
\quad\text{对数函数}\quad &\quad f(x)=\ln x & f'(x)=\frac{1}{x}\\
\\
\hline
\end{array}
- 定理: 常数関数 $f(x)=C$($C$ は実数である)の導関数は、$f'(x)=\frac{\mathrm{d}}{\mathrm{d}x}f(x)=\frac{\mathrm{d}}{\mathrm{d}x}C=0$ である。
- 定理:幂関数$f(x)=x^\alpha,\alpha\in\mathbb{R}$($α$は有理数)の導関数は、$f'(x)=\frac{\mathrm{d}}{\mathrm{d}x}f(x)=\frac{\mathrm{d}}{\mathrm{d}x}(x^\alpha)=\alpha x^{\alpha-1}$である。
- 定理:次の三角関数の微分は、それぞれ次の通りである。
\begin{aligned}
f(x)=\sin x, \qquad& f'(x)=\cos x\\
f(x)=\cos x, \qquad& f'(x)=-\sin x
\end{aligned}
- 定理:$f(x)$を$f(x)=a^x,a > 0,a\ne 1$とした時、f'(x)を計算すると$\frac{\mathrm{d}}{\mathrm{d}x}(a^x)=f'(x)=a^x\ln a$が得られる。特に$f(x)=e^x$の時、$f'(x)$は$\frac{\mathrm{d}}{\mathrm{d}x}(e^x)=f'(x)=e^x$である。
- 定理:$f(x)=\log_a x,a > 0, a\ne 1$とした時:$\frac{\mathrm{d}}{\mathrm{d}x}(\log_a x)=f'(x)=\frac{1}{x\ln a}$. 特に$f(x)=\ln x$の時に:$\frac{\mathrm{d}}{\mathrm{d}x}(\ln x)=f'(x)=\frac{1}{x}$.
関数の和、差、積、商の微分法則
- 定理[和、差]:関数$u=u(x)とv=v(x)$が$x$の点で微分可能なとき、以下が成り立つ:$[u(x)±v(x)]'=u'(x)±v'(x)$
- 定理[積]:もし関数$u=u(x)とv=v(x)$が$x$の点で微分可能なとき、次の式が成立する:$\left[u(x)v(x)\right]'=u'(x)v(x)+u(x)v'(x)$
- 定理[商]:もし関数$u=u(x), v=v(x)$が$x$点で微分可能でかつ $v(x)≠0$となるなら、以下が成り立つ:$\left[\frac{u(x)}{v(x)}\right]'=\frac{u'(x)v(x)-u(x)v'(x)}{v^2(x)}$
合成関数の導関数
- 定理(鎖式法則): もし$u=g(x)$が$x$点で微分可能で、$y=f(u)$が$u=g(x)$点で微分可能なとき、複合関数$y=f[g(x)]$が$x$点で微分可能であり、その導関数を以下のように表す:
\frac{\mathrm{d}y}{\mathrm{d}x}=f'(u)g'(x)\quad\text{または}\quad\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}u}\cdot\frac{\mathrm{d}u}{\mathrm{d}x}
第22回 微分と線形近似
曲線台形面積の一般的な解法
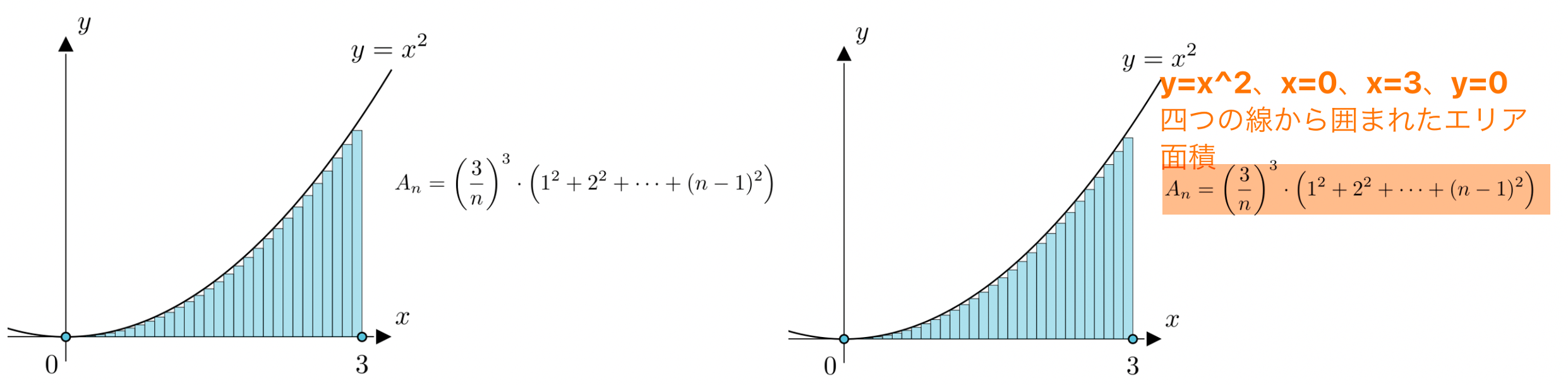
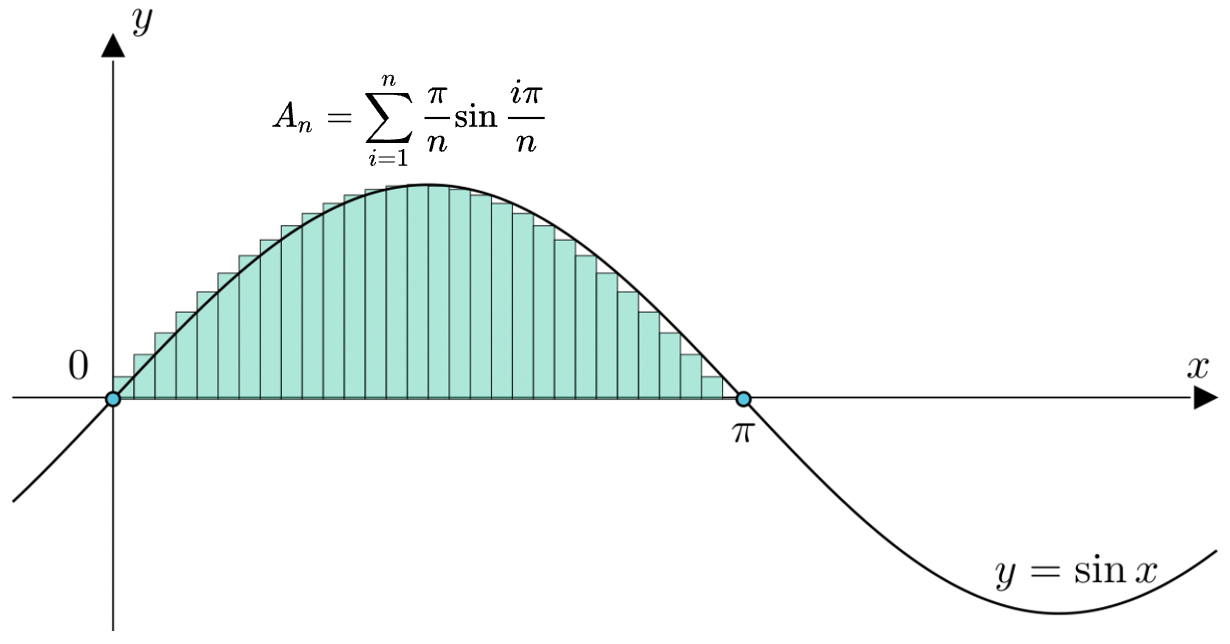
以下が二つ違う関数から作られた台形の面積の解く方法です。関数が違うと、解く方法も違うので、難しいです。
曲線台形の面積を一般的に解く方法が必要になります。
例1:
一般的な解く方法でしたら、曲線台形を線形近似にする必要があります。

関数曲線の線形近似
関数$f(x)$を$n$個の部分に分割し、それぞれを線分で近似する必要があります。これは関数の曲線の「線形近似」です。ある曲線の一部分に対して、それを近似するために使用される直線はその曲線の微分と呼ばれます。

第23回 導関数による微分の求め方
1.微分の定義
微分とは、局所的な曲線の線形近似であり、また微分は局所的な曲線を近似できる直線です。関数が与えられた点でどれだけ急峻に変化しているかを示す指標です。
厳格的な定義:
関数 $y = f(x)$ がある区間で定義されているとし、$x_0$ および $x_0 + Δx$ がこの区間に存在する場合、関数の増分:
$Δy = f(x_0 + Δx) - f(x_0)$
は以下のように表されます:
$Δy = AΔx + o(Δx)$
ここで、$A$ は $Δx$ に依存しない定数です。この場合、関数 $y = f(x)$ は点$ x_0$ において微分可能 であり、$AΔx$ は関数 $y = f(x)$ の点 $x_0$ における自立変数の増分 $Δx$ に対応する微分と呼ばれ、$\textrm{d}y$ と表記されます。つまり:
$\textrm{d}y = AΔx$
通常、$\mathrm{d}x$ = $Δx$ としますので、微分は $\textrm{d}y = A\mathrm{d}x$ と表されます。
$o(Δx)$: 高次の無限小 $o(Δx)$ の定義は、前述の差分が $x_0$ に近づくほど差分が小さくなることを意味します。
2.導数の定義
導数は、関数の微分を表す数学的な概念です。ある点における導数は、その点における関数の微小変化率を表します。導数は、関数の微分可能性とその変化の速さを評価するために使用されます。
導数は、実際に微分の勾配です。したがって、
- 微分が存在する場合、必ず導数も存在し、その逆も同様です。
- つまり、微分可能ならば導数も可能であり、導数可能ならば微分も可能です。
3.左導数、右導数
関数がある点で微分可能である場合、その点における左側と右側の微小変化率をそれぞれ左導数と右導数と呼びます。
- 左導数は点の左側からのアプローチにおける変化率を表し、
- 右導数は点の右側からのアプローチにおける変化率を表します。
関数 $f(x)$ が $x_0$ の左側と右側で導関数が存在し、等しい場合、関数 $f(x)$ は $x_0$ で微分可能である。
4.連続と可微分
可微分性は、関数がある点で微分可能であることを示します。連続性は微分可能性の必要条件であり、微分可能な関数は連続である必要がありますが、連続な関数が必ずしも微分可能であるとは限りません。
- 微分可能 $→$ 連続
- 連続 $\neq →$ 微分可能
5.接線と割線
微分は、関数の接線の傾きを求めるために使用されます。ある点における関数の微分値は、その点での接線の傾きに対応します。接線は、関数のグラフ上のある点で接する直線です。
曲線の微分は、その曲線を近似する直線のことを指し、接線とも呼ばれます。
新しい座標系の原点は、その接線が関数曲線上を通る点であり、したがってその原点は接点・切点(せってん)とも呼ばれます。新しい座標系は切点座標系とも呼ばれます。以下は図で示されています。
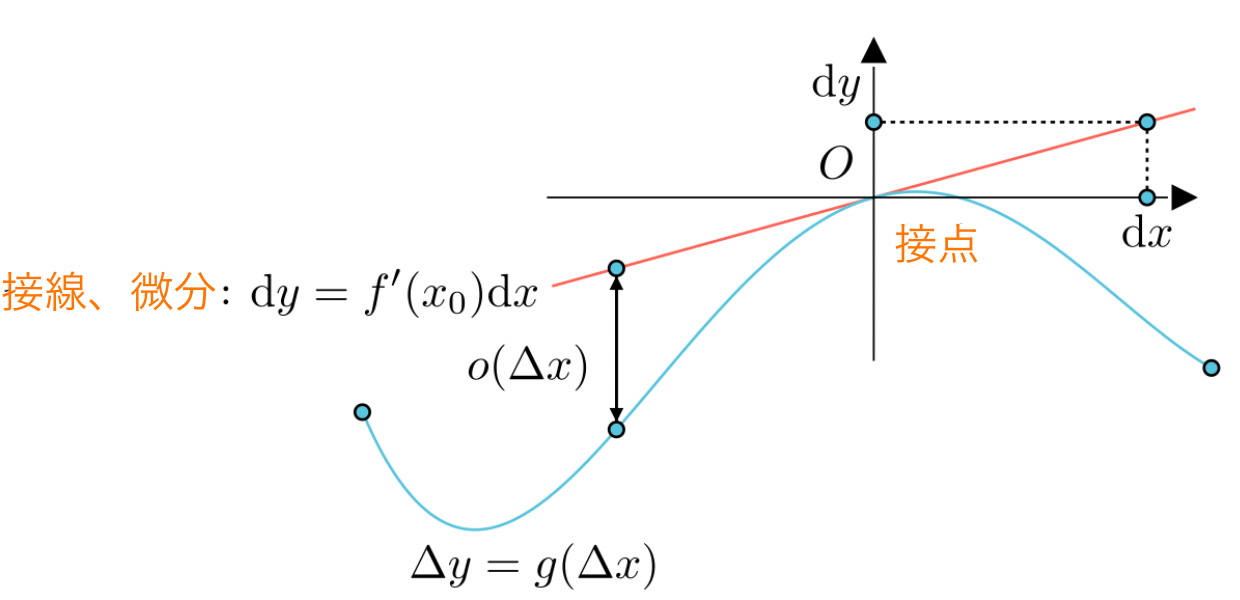
接線(微分)を除いた、曲線 $y=f(x)$ の他の点$(x_0, f(x_0))$を通る直線は、割線(かっせん) と呼ばれます。以下の図のような直線$ y=g(x) $が割線の例です。
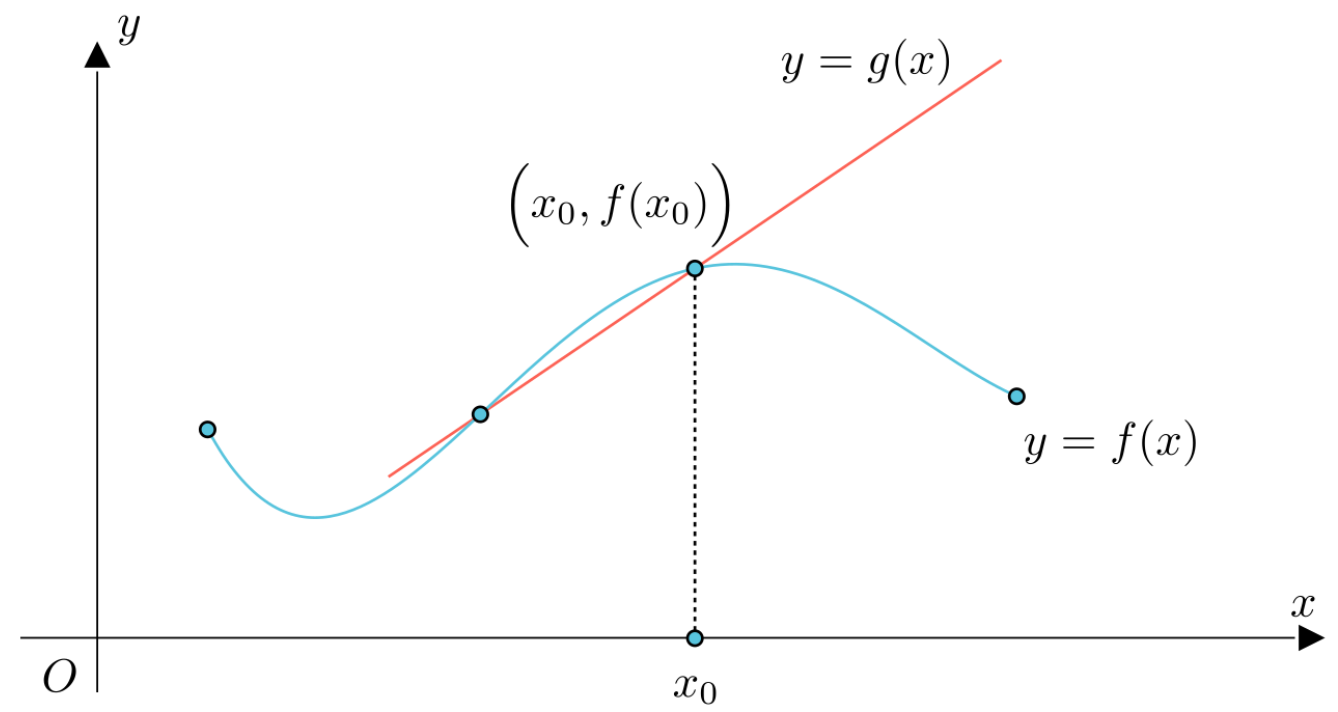
- 割線$y=g(x)$と曲線$y=f(x)$の間の差は、$Δx$と同じ次数の無限小量$α$ です。
- 接線$y=g(x)$と曲線$y=f(x)$の間の差は、$Δx$の高い次数の無限小量$o(Δx)$ です。
第24回 一般的な導関数
定義:若開区間Iのすべての点において $y=f(x)$ が微分可能であるとき、$y=f(x)$は開区間$I$内で微分可能(可微)という。
このとき、$I$内の任意の $x$ に対応する $f(x)$ の唯一の決定的な導関数の値が存在することから新しい関数 $f(x)$ の導関数 が構成される。そして、この関数は$y'、f'(x)$、$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}$、あるいは$\displaystyle\frac{\mathrm{d}f(x)}{\mathrm{d}x}$と言われ、以下の式で定義される。
y'=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\quad\text{または}\quad f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}
第25回 関数の和、差、積、商の微分法則
- 例題:
第26回 合成関数の導関数
- 例題:
第27回 逆関数の導関数
定理:もし$x=f(y)$が$Iy$の区間内で厳密に単調で、微分可能でかつ$f'(y)≠0$であるならば、その逆関数$y=f^{-1}(x)$は$Ix ={x|x=f(y), y∈Iy}$の区間内で微分可能である。また次が成り立つ:
[f^{-1}(x)]'=\frac{1}{f'(y)}\quad\text{または}\quad\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{1}{\frac{\mathrm{d}x}{\mathrm{d}y}}
第28回 陰関数の導関数
- 显関数: $x+y^3-1=0\implies y=\sqrt[3]{1-x}$
- 陰関数: $y^5+2y-x-3x^7=0 \implies ❌(y=xの形で表すことができない) $
- 練習
第29回 パラメー方程式の導関数と関連する変化率
第30回 高階導関数
書き方:
参考情報: