本記事は数学講座2.19閉区間上の連続関数の性質を勉強して投稿したメモです。詳細は元の素晴らしい講座のページをチェックしてください。
閉区間上の連続関数
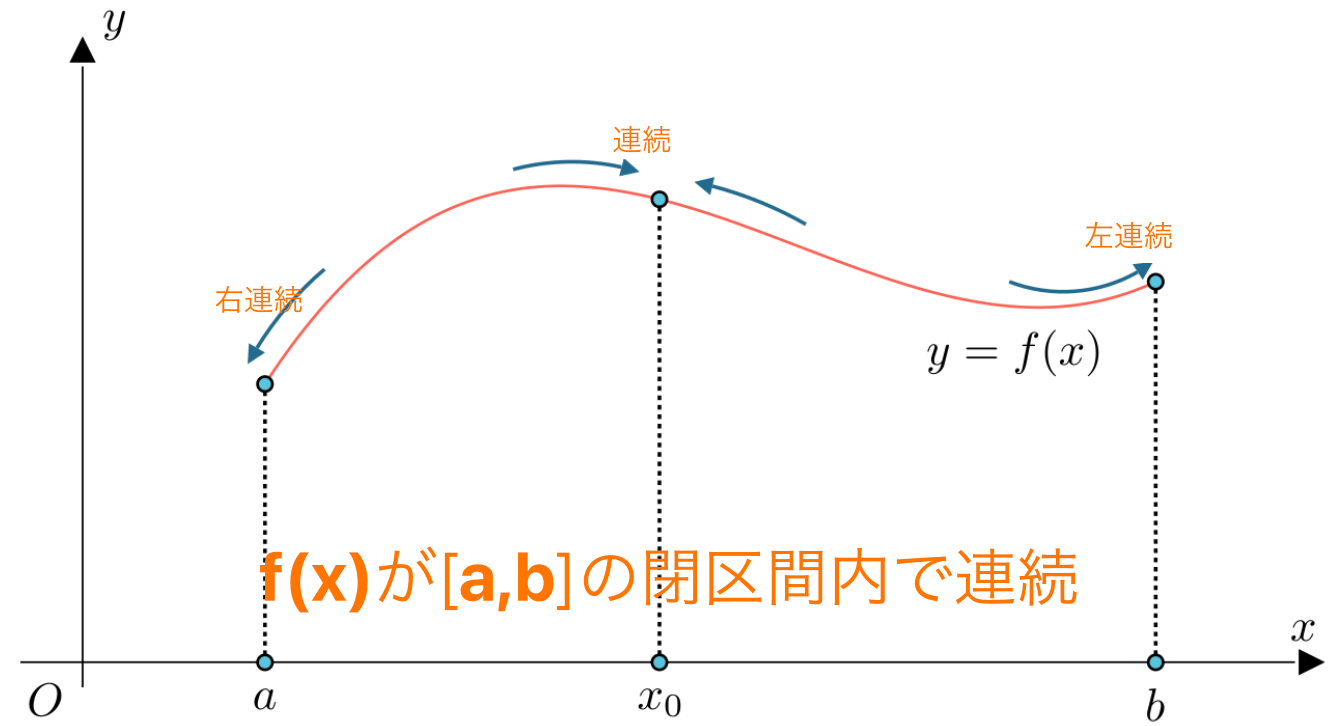
定義:
関数 $f(x)$ が開区間 $(a,b)$ 上で連続であり、左端点 $a$ で右連続であり、右端点 $b$ で左連続である場合、関数 $f(x)$ は閉区間 $[a,b]$ 上で連続です。
最大値、最小値
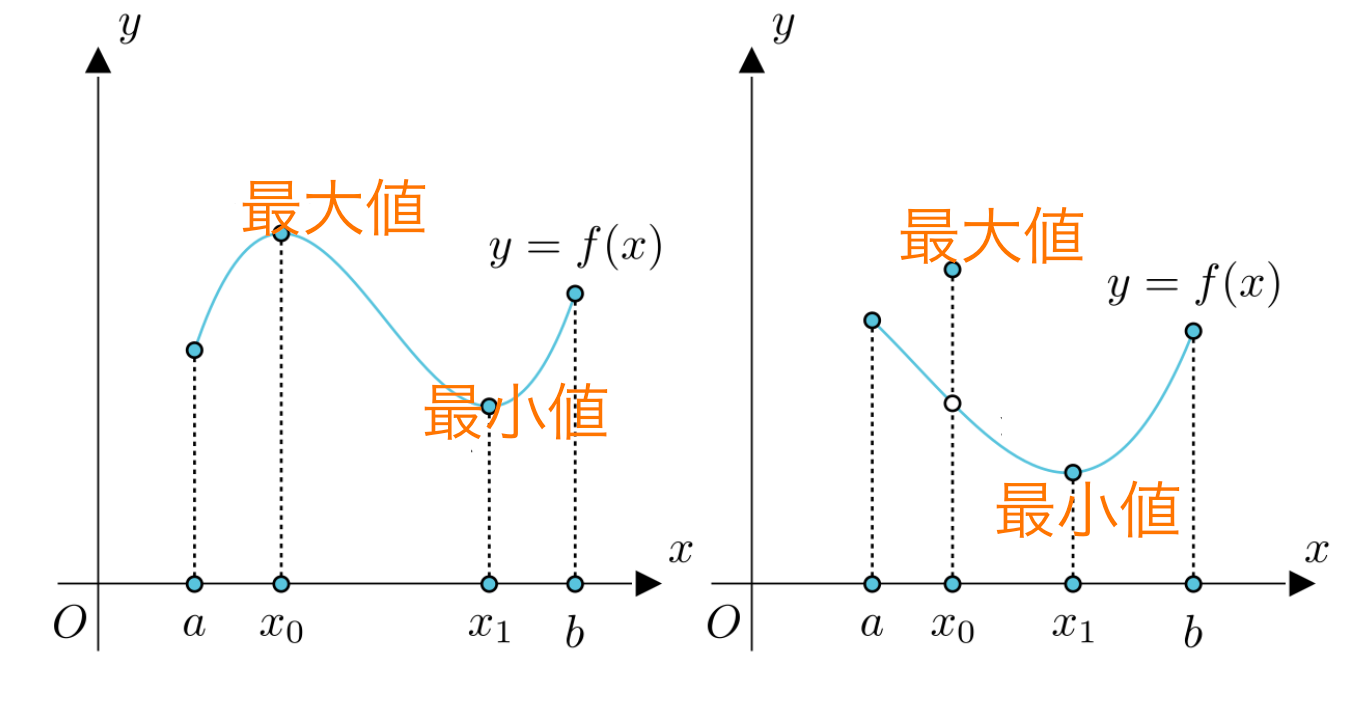
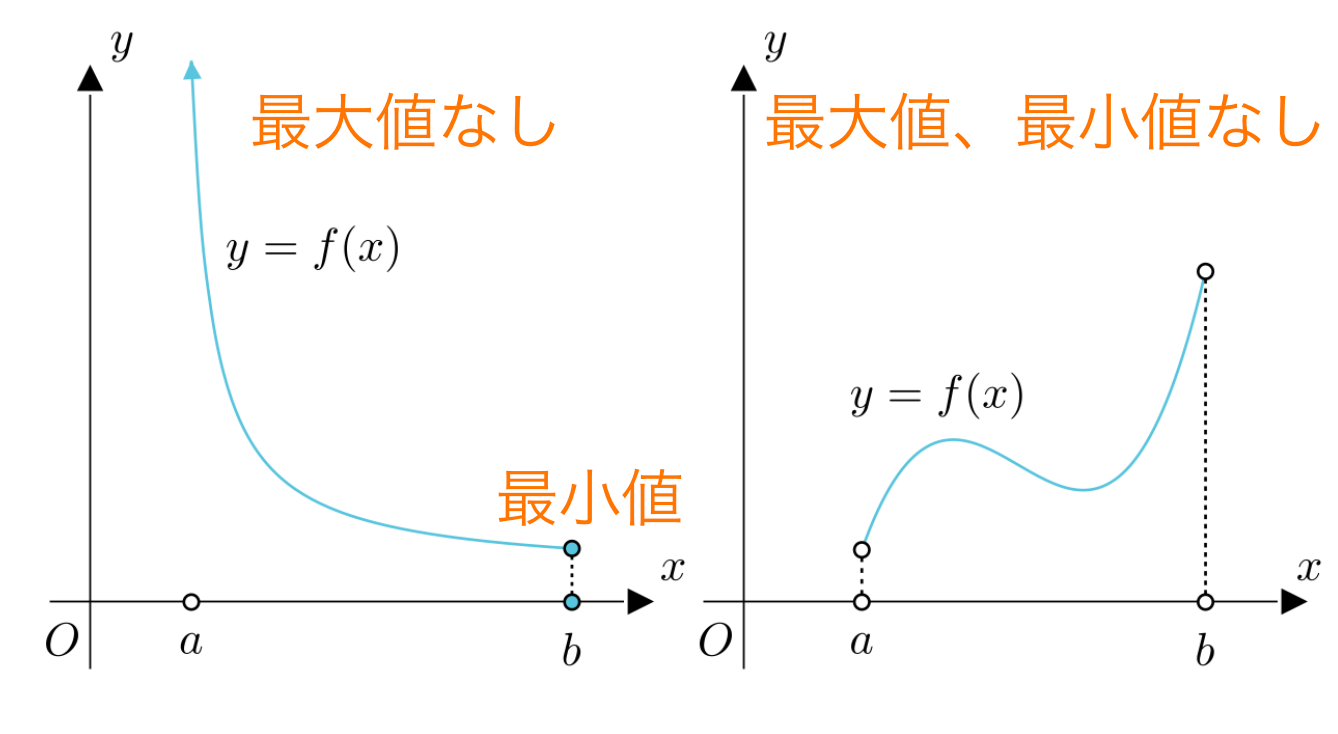
空間内の最大値、最小値:
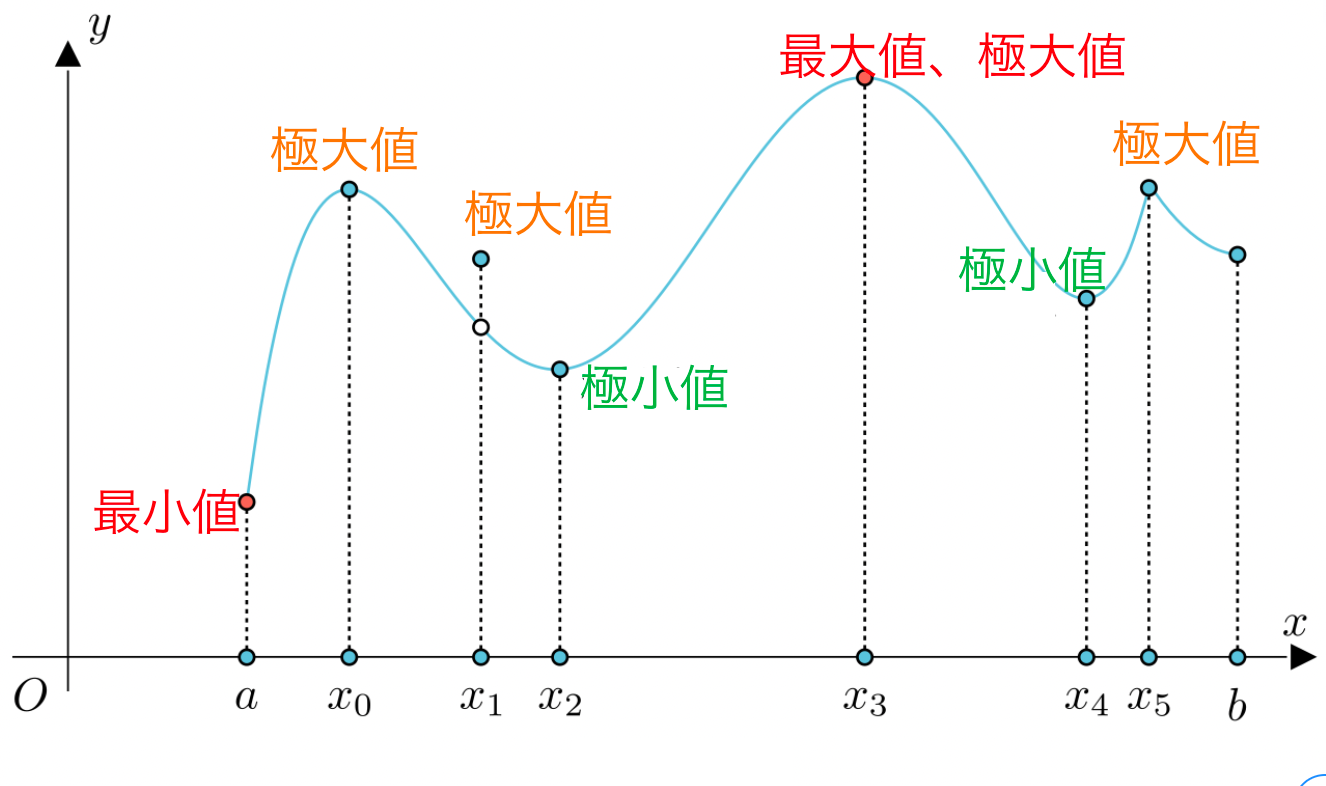
極大値、極小値
最大値は区間I上のグローバルな概念であり、極値は近傍上の局所的な概念です。
有界性と最大値最小値定理 (ゆうかいせいとさいだいちさいしょうちていり)
定理:
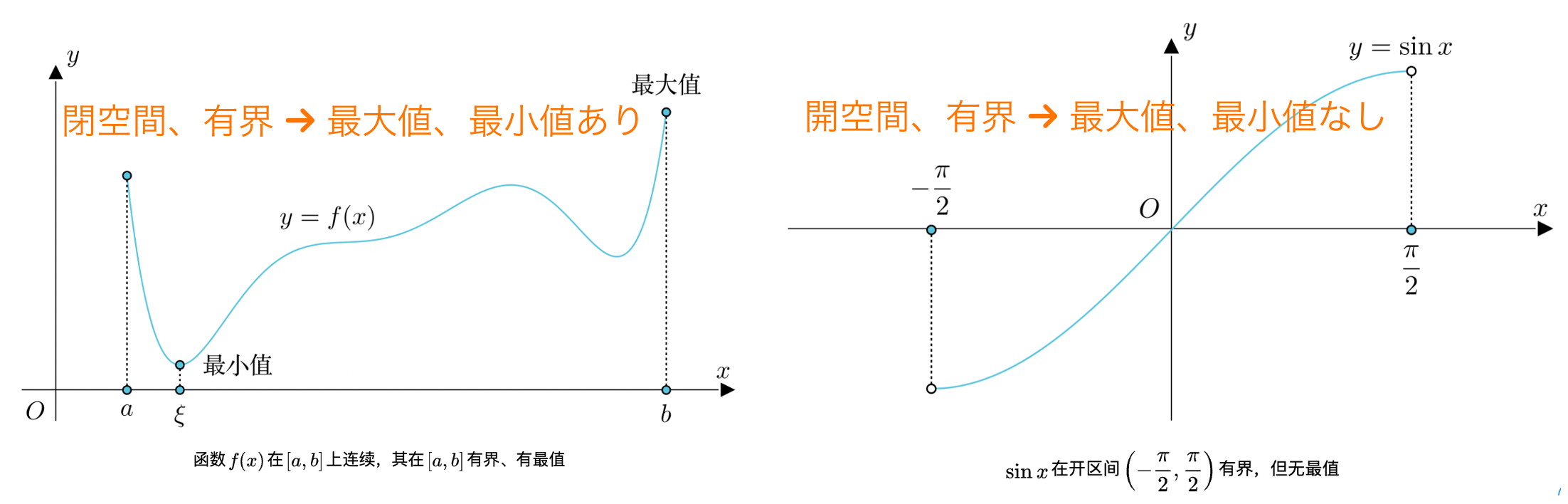
閉区間上の連続関数は、その区間上で有界であり、必ず最大値と最小値を取る。
零点定理
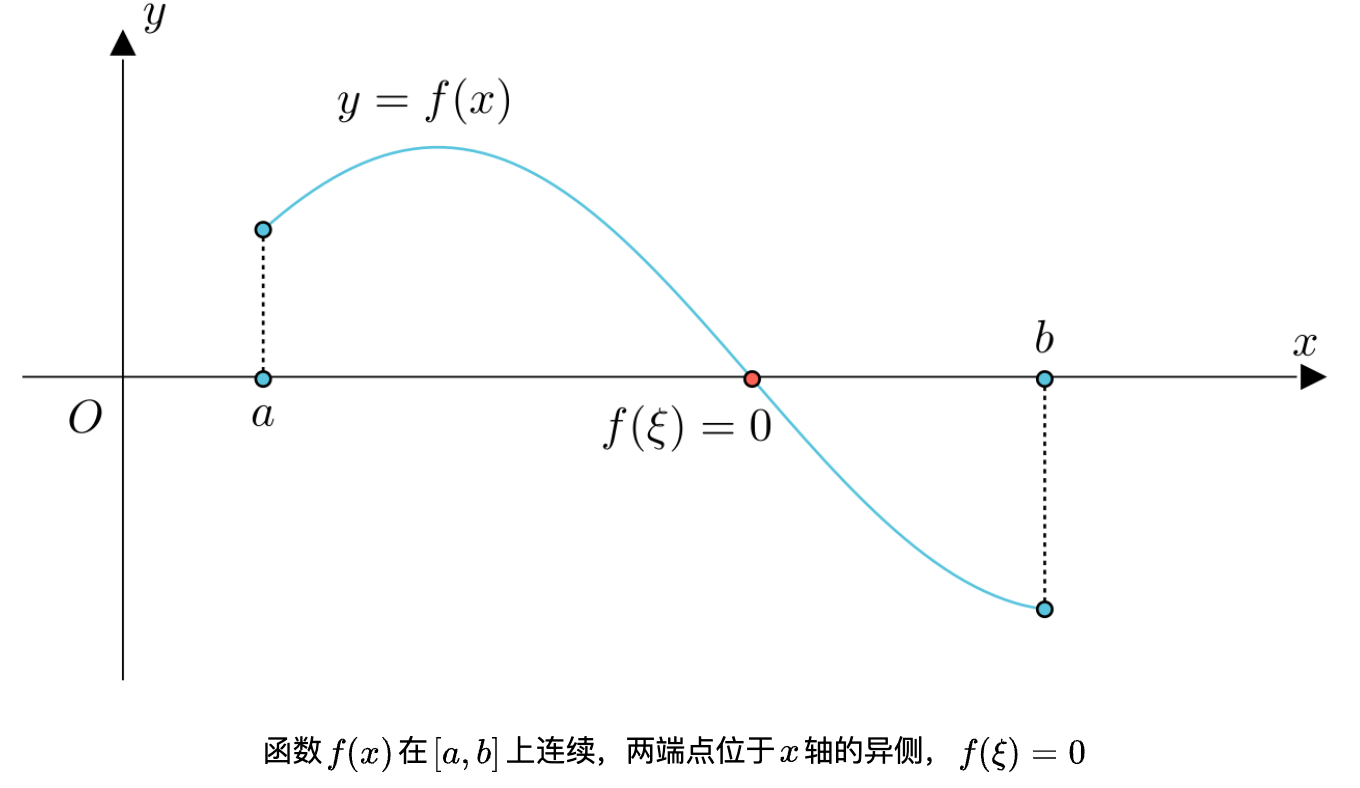
定理(零点定理):
関数$y=f(x)$が閉区間$[a,b]$上で連続であり、かつ$f(a)とf(b)$が異符号(つまり、$f(a)・f(b) < 0$)である場合、開区間$(a,b)$内には少なくとも1点$ξ$が存在し、$f(ξ) = 0 $となる。
介値定理 (かいちていり)
定理(中間値の定理):
関数$f(x)$が閉区間$[a,b]$上で連続であり、この区間の端点で異なる関数値を取る場合、つまり:
$f(a) = A, f(b) = B, A ≠ B$
このとき、$AとB$の間の任意の数$C$に対して、開区間$(a,b)$内には少なくとも1点$ξ$が存在し、$f(ξ) = C$ となる。
定理:
閉区間$[a,b]$上で連続な関数$y=f(x)$の値域は閉区間$[m,M]$であり、$mとM$はそれぞれ$f(x)$が$[a,b]$上で取る最小値と最大値です。
参考情報