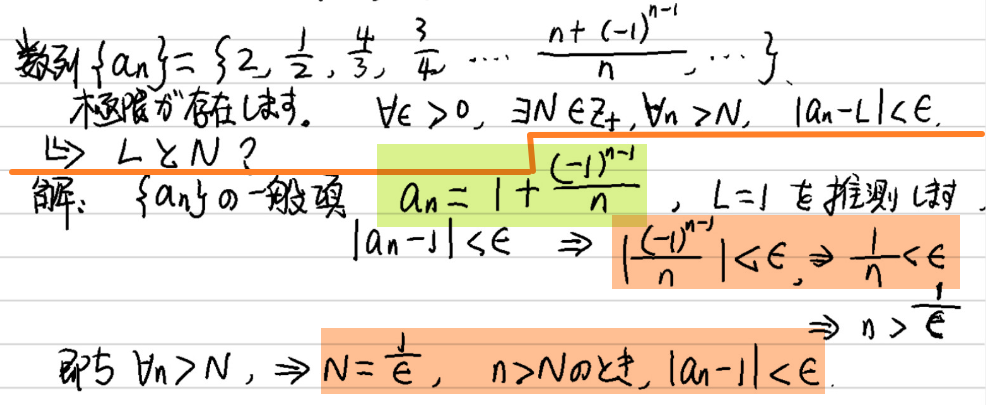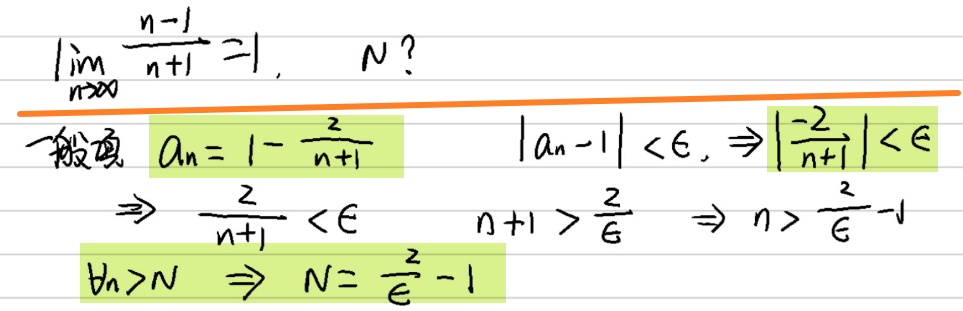本記事は数学講座2.2ワイエルシュトラス数列の極限を勉強して投稿したメモです。詳細は元の素晴らしい講座のページをチェックしてください。
コーシー数列の極限の問題
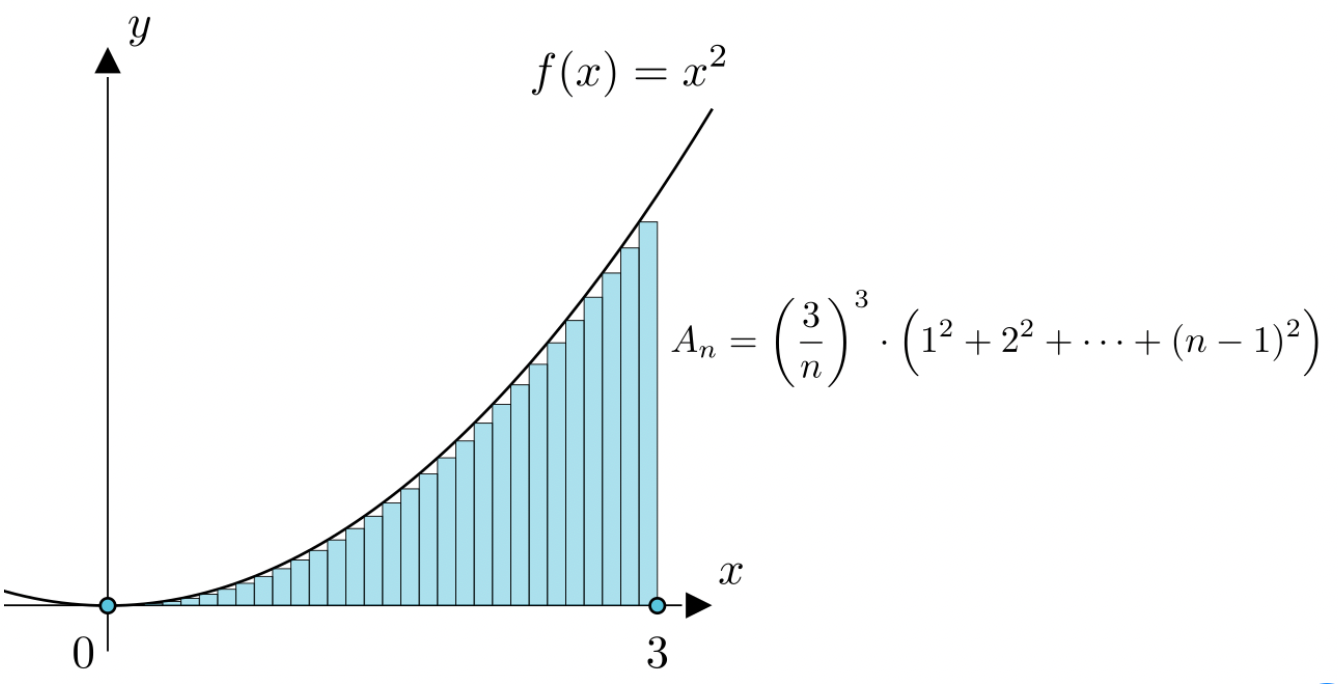
\begin{aligned}\text{長方形の和を利用して}\ \\\text{曲辺台形を擬似する}\end{aligned}\longrightarrow \text{長方形和一般項}\ A_nを算出\longrightarrow \begin{aligned}\lim_{n\to\infty}A_n=Aを利用して\quad\\\text{曲辺台形の面積Aを算出する}\ \end{aligned}
\ \
コーシー数列を利用して、曲辺台形面積を算出しようとしたが、$\displaystyle\lim_{n\to\infty}A_n$の計算方法がまだ分からないです。
数列極限の厳密な定義
定義:
数列{${a_n}$}に対して、実数$L$が存在し、任意の正の実数$\epsilon$(いくら小さくても)に対して、ある正の整数$N$が存在して、すべての$n > N$に対して以下の条件が成り立つ場合、
$|a_n-L| < \epsilon,\quad L\in\mathbb{R}$
このとき、$L$は数列${a_n}$の「極限」と呼ばれ、また数列${a_n}$は$L$に「収束する」と言われ、以下のように表記されます:
\lim_{n\to\infty}a_n=L\quad\text{または}\quad a_n\to L(n\to \infty)
もし定数Lが存在しない場合、数列${a_n}$は「極限を持たない」と言われ、また数列${a_n}$は「発散する」とも言われます。また、$\displaystyle\lim_{n\to\infty}a_n$が存在しないとも言えます。
例:
$\epsilon$がどんなに小さくても、常に適切な$N$を見つけることができ、$n > N$の場合、常に$|a_n-L| < \epsilon$が成り立ちます。
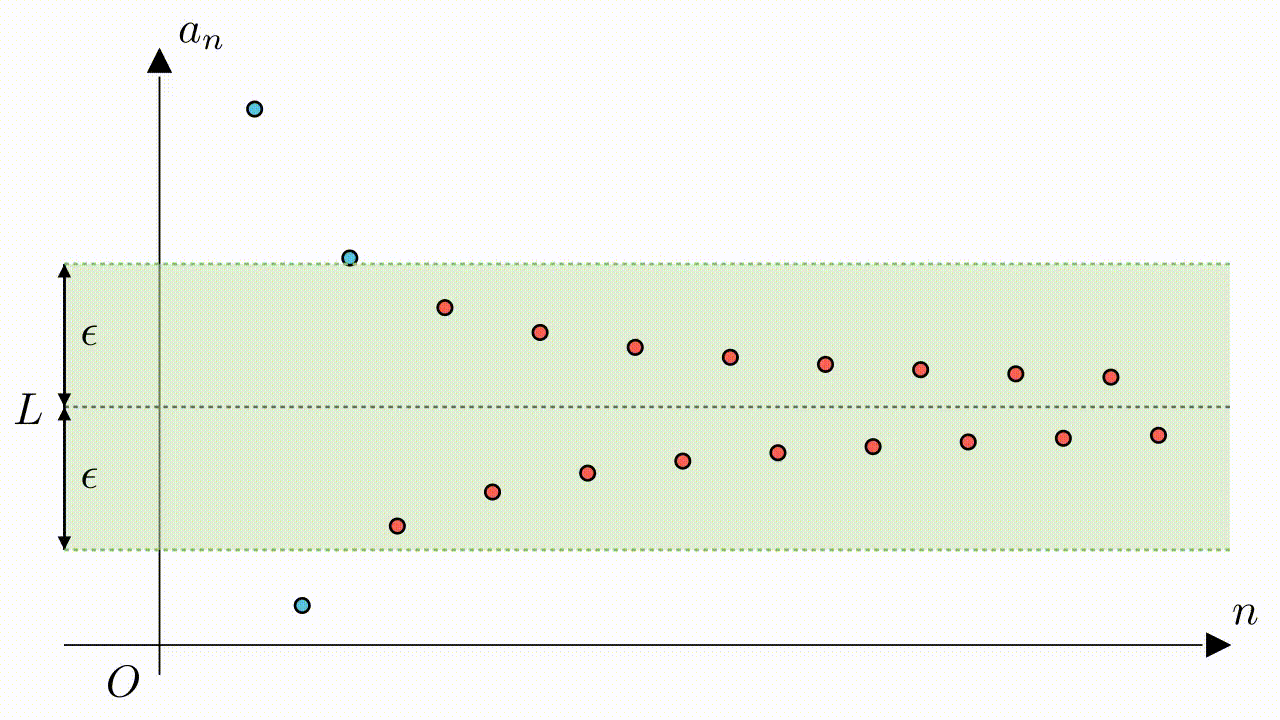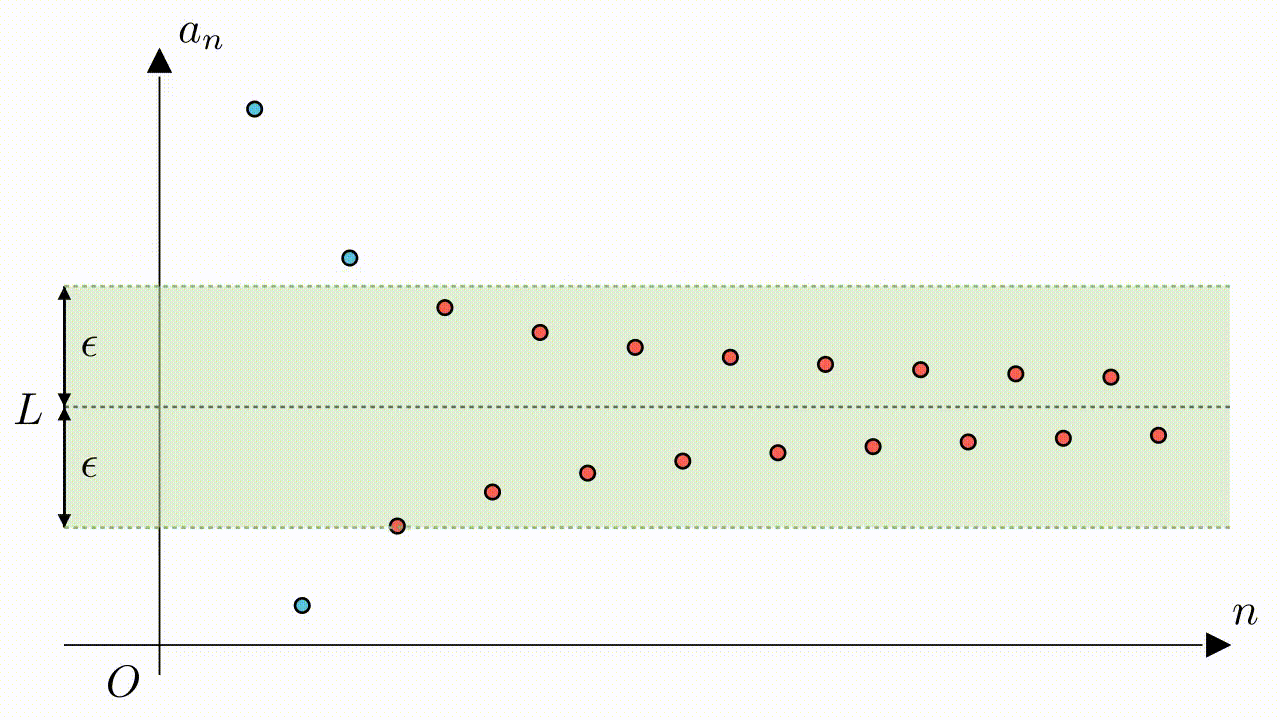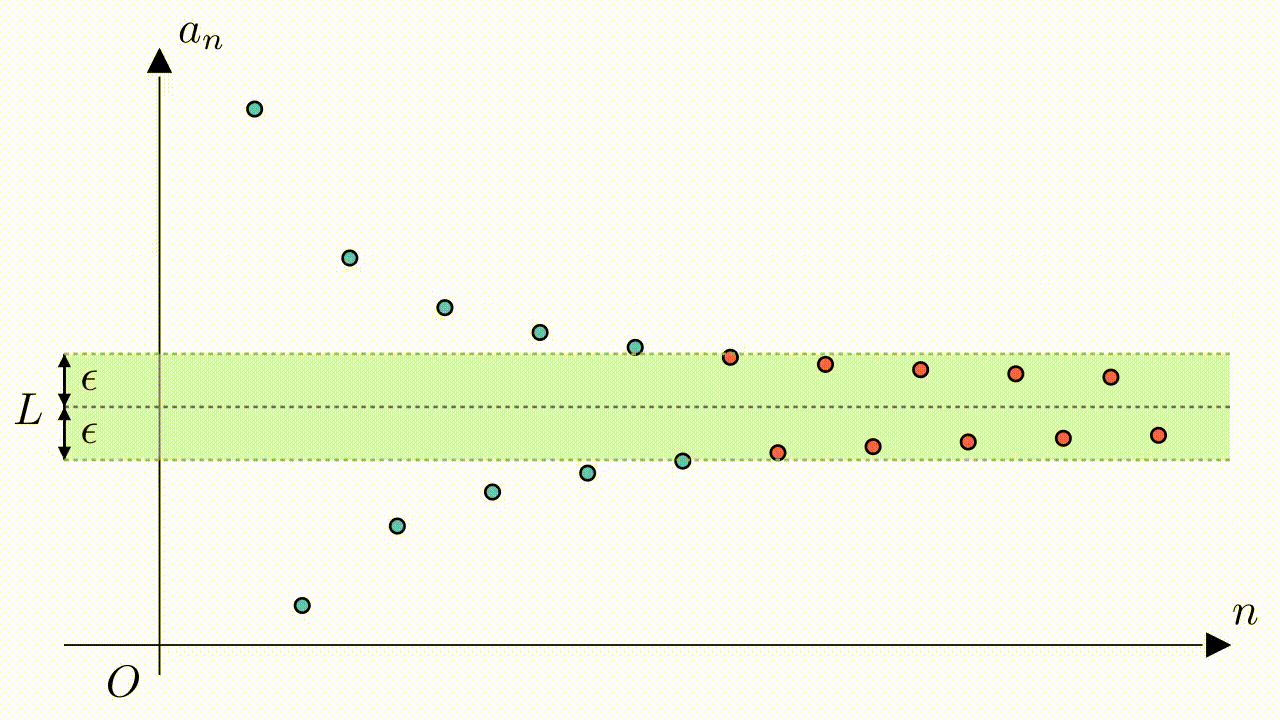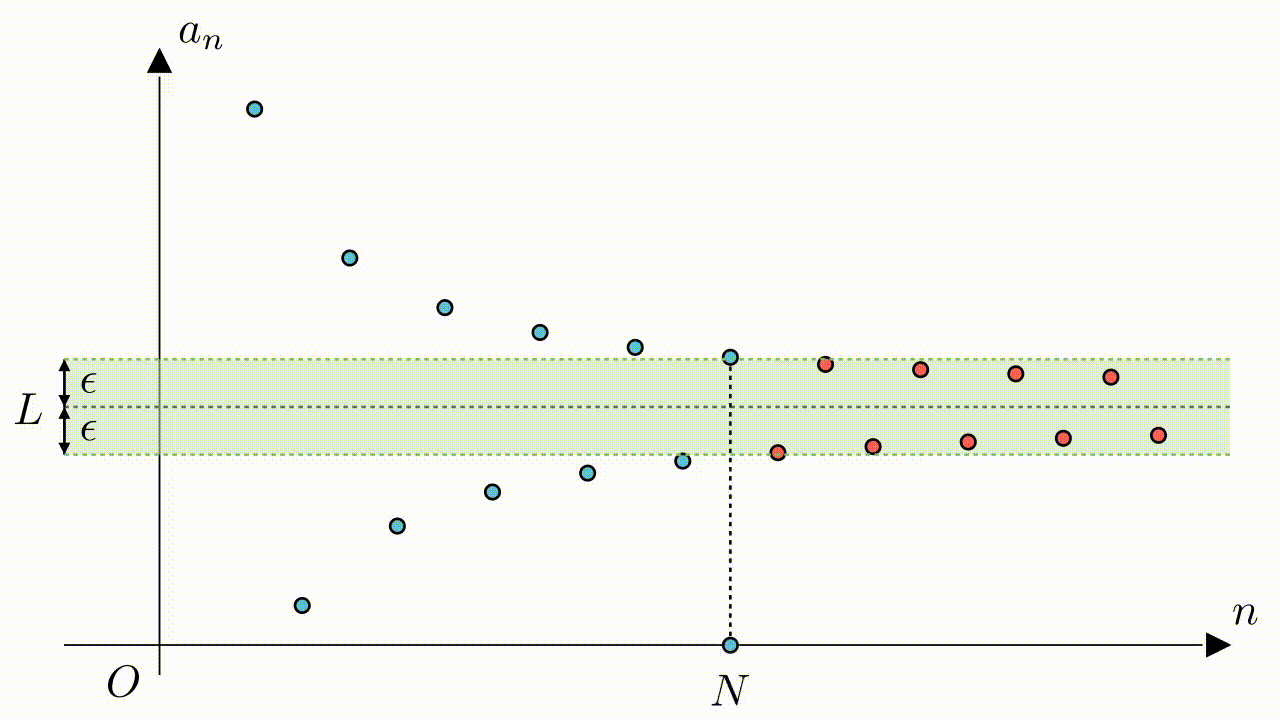
数列極限のもう一つ定義
こちらで論理記号を使います。
\begin{array}{c|c|c}
\hline
\quad \text{論理記号}\quad&\quad \text{意味}\quad& \quad\text{解釈}\quad\\
\hline
\\
\quad\color{orange}\forall\quad&\quad\text{任意}\quad& \quad\text{ Any}\quad \\
\color{blue}\exists& \text{存在} & \text{Exist}\\
\\
\hline
\end{array}
例:
\begin{array}{c|c}
\hline
\quad \text{論理記号}\quad&\quad \text{意味}\quad\\
\hline
\\
\quad\forall \epsilon > 0\quad&\quad\text{任意の正数}\ \epsilon\quad\\
\quad\exists N\in\mathbb{Z}^{+}\quad&\quad\text{存在する}\ N\quad\\
\quad\forall n > N\quad&\quad\text{全ての}\ n > N\quad\\
\\
\hline
\end{array}
以上の定義を上記の論理記号で表すと:
数列{${a_n}$}に対して、$\forall \epsilon > 0$、$\exists N\in\mathbb{Z}^{+}$、$\forall n > N$:
|a_n-L| < \epsilon,\quad L\in\mathbb{R}
このとき、$L$は数列{${a_n}$}の「極限」と呼ばれ、また数列${a_n}$は$L$に「収束する」と言われ、以下のように表記されます:
\lim_{n\to\infty}a_n=L\quad\text{または}\quad a_n\to L(n\to \infty)
もし定数Lが存在しない場合、
- 数列${a_n}$は「極限を持たない」と言われ、
- また数列${a_n}$は「発散する」とも言われます、
- また、$\displaystyle\lim_{n\to\infty}a_n$が存在しないとも言えます。
例題:
${a_n}={0.9,0.99,0.999,\cdots}$には、極限があります。即ち、$\forall \epsilon > 0$、$\exists N\in\mathbb{Z}^{+}$、$\forall n > N$の時に、$|a_n-L| < \epsilon$があります。$LとN$を解けてください。
解:
極限$L=1$を推測します、これを使って検証してみます。
数列の一般項が$\displaystyle a_n=1-\frac{1}{10^n}$、$L=1$、また$|a_n-L| < \epsilon$が成立するので、以下のがあります:
|a_n-L|=|a_n-1|=|1-\frac{1}{10^n}-1|=\frac{1}{10^n} < \epsilon\implies n > \lg\frac{1}{\epsilon}
即ち、$\displaystyle N=\lceil\lg\frac{1}{\epsilon}\rceil$、$n > N$のときに、$|a_n-1| < \epsilon$が成立します。
よって、$L=1,\displaystyle N=\lceil\lg\frac{1}{\epsilon}\rceil$になります。
練習
参考情報