本記事は数学講座2.4無限に近づく関数の極限を勉強して投稿したメモです。詳細は元の素晴らしい講座のページをチェックしてください。
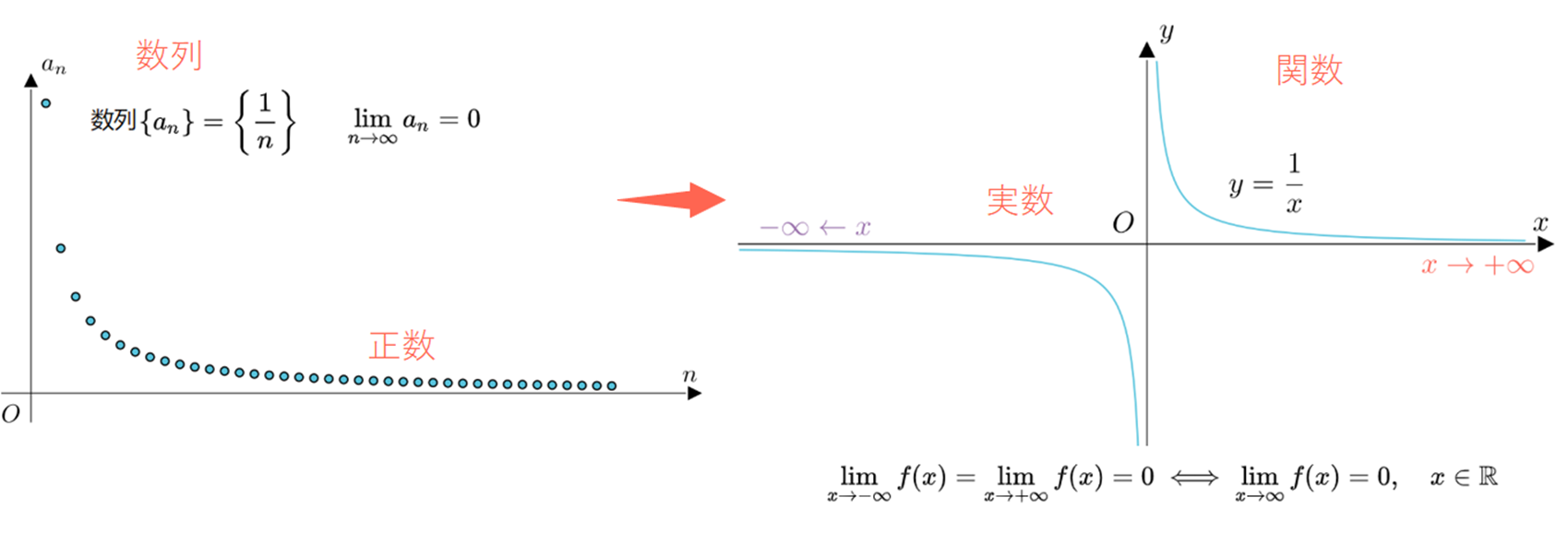
離散から連続へ
関数は数学の中で最も研究されている対象ですので、このレッスンでは、数列の極限を無限に近づく関数の極限にします。
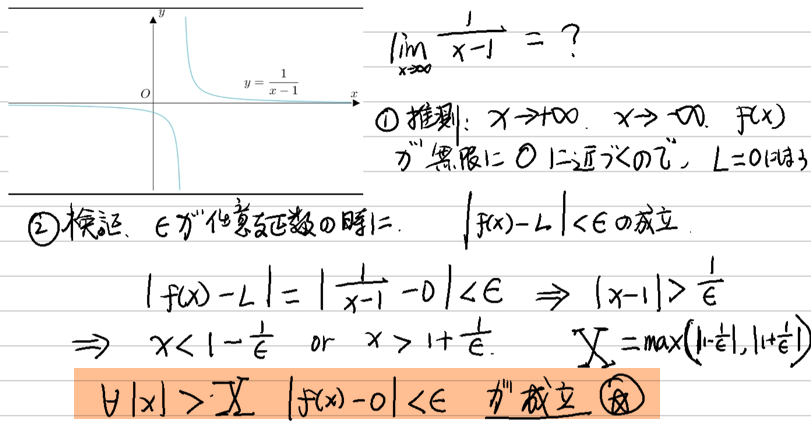
無限大になる関数の極限
元々数列に関する定義では、正数の$N$なので、関数の極限定義になると、定義も変更が必要です。
定義:
$|x|$ が某正数より大きいときに、関数 $f(x)$があります。
もし、$\forall \epsilon > 0$ 、$\exists X > 0 $、$\forall |x| > X $に対して以下が成り立つ場合:
$|f(x)-L| < \epsilon,\quad L\in\mathbb{R}$
そのとき、$L $を関数 $f(x) の x $が無限大に向かうときの 極限 と呼びます。また、$x$ が無限大に向かうとき関数$ f(x) が L $に 収束 するとも言い、以下のように表します:
$\lim_{x\to\infty}f(x)=L\quad\text{または}\quad f(x)\to L(x\to \infty)$
もし、このような定数$ L $が存在しない場合、関数 $f(x) $が $x $が無限大に向かうとき 極限 を持たないと言い、または関数 $f(x) $が 発散 すると言います。また、$\displaystyle\lim_{x\to\infty}f(x)$ が存在しないとも言います。
関数の極限定義は、数列と同じなのは、まず極限値$L$を推測してから、この$L$を検証します。
違うところは:
\begin{array}{c|c}
\hline
\quad \text{数列極限} \quad\quad&\quad x\to\infty\ \text{の関数極限}\quad \\
\hline \\
\text{数列}\ \{a_n\} &\quad \text{関数}\ f(x)\ \text{が}\ |x|\ \text{某正数より大きいとき存在}\quad\\
\exists N\in\mathbb{Z}^{+} & \exists X > 0\\
\forall n > N & \forall |x| > X\\
\\
\hline
\end{array}
無限大になる関数の極限例
正の無限大、または負の無限大になる関数の極限
正の無限大、または負の無限大になる関数の極限、無限大になる関数の極限、これら三つの定義がほとんど同じです。
違いところは、$x$の範囲です。
\begin{array}{c|c|c}
\hline
\quad x\to\infty\ \text{関数極限} \quad&\quad x\to+\infty\ \text{関数極限} \quad&\quad x\to-\infty\ \text{関数極限}\quad \\
\hline\\
|x|\ \text{>某正数} & x\ \text{>某数} & x\ \text{<某数}\\
\forall |x| > X & \forall x > X & \forall x < -X\\\\
\hline
\end{array}
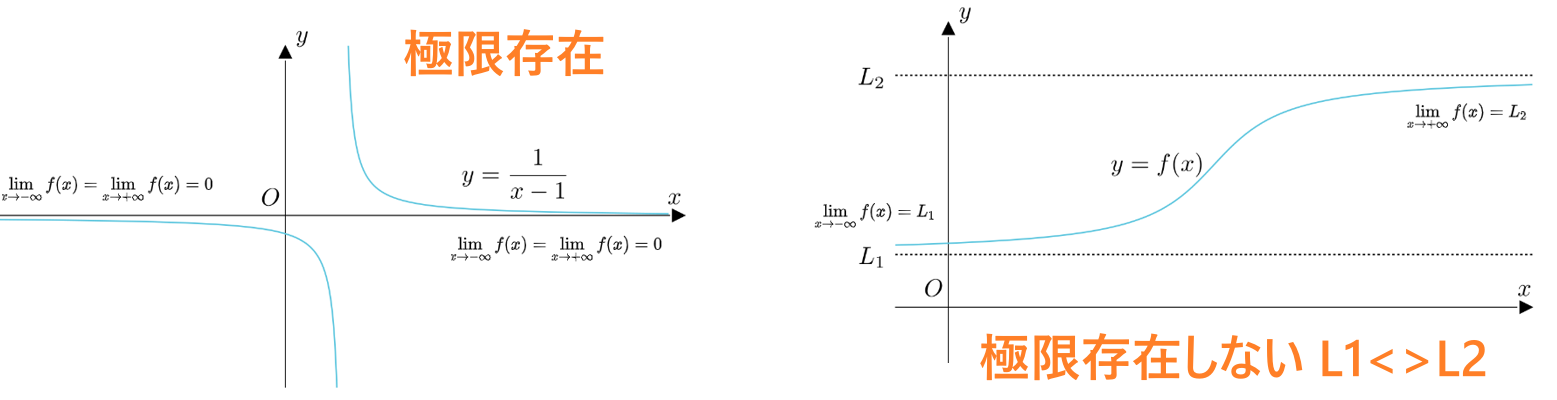
無限大の極限が存在するための十分条件
無限大になる関数の極限が存在の充分必要な条件が:正の無限大、または負の無限大になる関数の極限が存在且つ同じです。
\lim_{x\to-\infty}f(x)=\lim_{x\to+\infty}f(x)=L\iff\lim_{x\to\infty}f(x)=L
以下の例を参照: