本記事は数学講座2.12合成関数の極限を勉強して投稿したメモです。詳細は元の素晴らしい講座のページをチェックしてください。
合成関数の極限
定義:
\left.\begin{aligned}
\lim_{x\to x_0}g(x)=u_0\\
\lim_{u\to u_0}f(u)=L\\
x\in\mathring{U}(x_0)\ \text{の時}\ y=f[\ g(x)\ ]\ \text{定義あり}\\
x\in\mathring{U}(x_0)\ \text{の時}\ g(x)\ne u_0
\end{aligned}\right\}\implies \lim_{x\to x_0}f[\ g(x)\ ]=\lim_{u\to u_0}f(u)=L
例1:
$\displaystyle\lim_{x\to 4}\frac{\sin(x-4)^2}{(x-4)^2}$を解く。
解く:
\left.\begin{aligned}
\lim_{x\to 4}g(x)=\lim_{x\to 4}(x-4)^2=0\\
\lim_{u\to 0}f(u)=\lim_{u\to 0}\frac{\sin u}{u}=1\\
x\in\mathring{U}(4)\ \text{の時}\ y=f[\ g(x)\ ]\ \text{定義あり}\\
x\in\mathring{U}(4)\ \text{の時}\ g(x)\ne 0
\end{aligned}\right\}\implies \lim_{x\to 4}\frac{\sin(x-4)^2}{(x-4)^2}=\lim_{x\to 4}f[\ g(x)\ ]=\lim_{u\to 0}\frac{\sin u}{u}=1
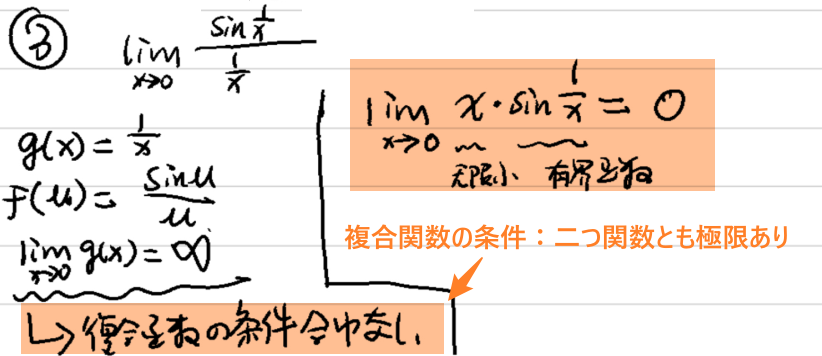
例2:
例3:
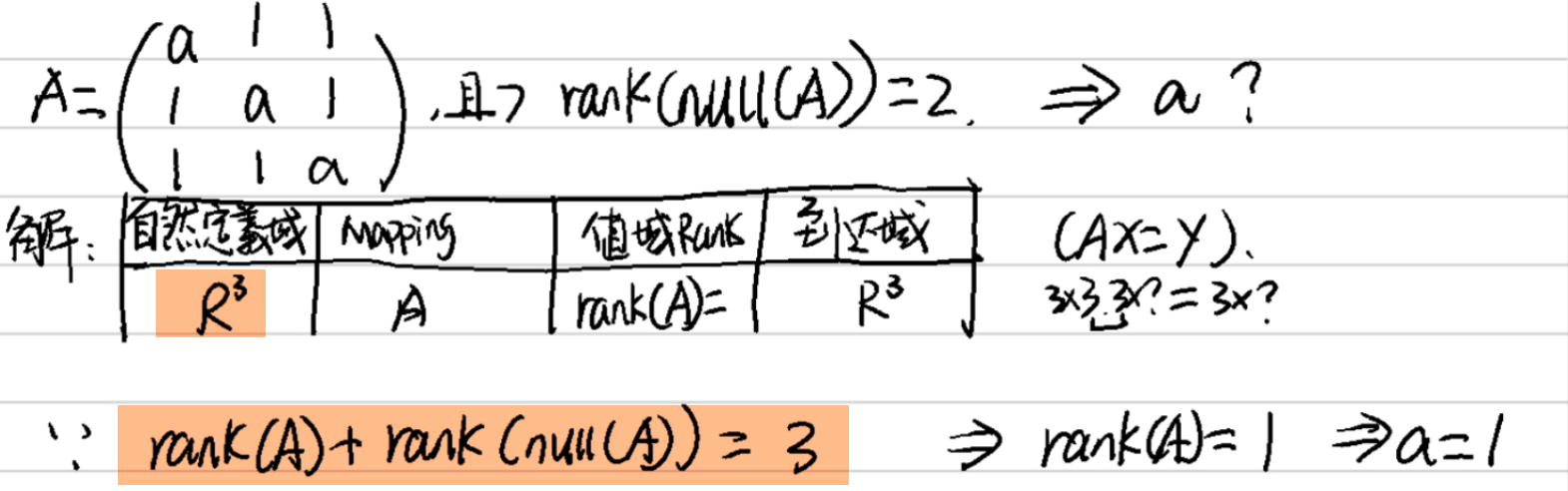
練習
参考情報