本記事は以下の数学講座2.1 ベクトル / 2.2 ベクトルの加算、減算、およびスカラー倍を勉強して投稿したメモです。詳細は元の素晴らしい講座のページをチェックしてください。
ベクトルはベクトル空間(又は線形空間)の構成要素であり、非常に基礎的且つ重要な概念です。
[まとめ] ベクトルのスカラー倍と加算
ベクトルのスカラー倍と加算
有向線分
ベクトルは、始点と終点を持った有向線分で、大きさと向きを持ちます。例えば力、速度、加速度、変位などがあり、これらは有向線分を用いて表現されます。
例えば、バスケットボールの瞬間速度$v(t)$はベクトルであり、下の図のように矢印のついた有向線分で表すことができます。その長さは瞬間速度の大きさを表し、矢印は瞬間速度の向きを指します。

二つのベクトルの大きさと向きが同じであれば、それらのベクトルは等しいと考えます(位置は気にしなくてもよいです)。

ベクトルの定義
n個の並べられた数$a_1$,$a_2$,...,$a_n$から成る配列を$n$次元ベクトルと呼び、これら$n$個の数をベクトルの$n$個の成分と呼びます。$i$番目の数$a_i$はi番目の成分と呼ばれます。$n$次元ベクトルは、列として書くことも、行として書くこともでき、それぞれ列ベクトルと行ベクトルと呼ばれます。
- $n$次元列ベクトル:
\left(
\begin{array}{}
a_{1}\\
a_{2}\\
\vdots\\
a_{n}
\end{array}
\right)
- $n$次元行ベクトル:
\left(
\begin{array}{}
a_{1},a_{2}...a_{n} \
\end{array}
\right)
2次元ベクトル
2次元ベクトル
u = \left(\begin{array}{}u_{1}\\u_{2}\\\end{array}\right)
は直交座標系上の点です。また、原点から$u$に向かう有向線分です。

上記の2つの幾何学的意味は完全に同等です。
3次元ベクトル
3次元ベクトルも同様で、前のセクションで言及したバスケットボールは、3次元空間の1点として、それ自体がベクトルであり、原点からその点へ向かう有向線分をベクトルと見なすこともできます。

n次元ベクトル
より高次元のベクトルに関しては、例えばゲームキャラクターの情報を表現したい場合などがあります。

以上のキャラクターの情報を10次元のベクトルで表現できます。しかし、幾何学的意味がないです。
\left(
\begin{array}{}
1477\\
Lv38.79 \\
\vdots\\
3.75\\
0\\
\end{array}
\right)
もし2つのベクトルの次元が同じで、それぞれの要素が等しい場合、これら2つのベクトルは等しいと見なされます。
\begin{pmatrix}
1\\2\end{pmatrix}
=
\begin{pmatrix}
1\\2\end{pmatrix}
,
\quad
\begin{pmatrix}
1\\2\end{pmatrix}
\ne
\begin{pmatrix}
2\\4
\end{pmatrix}
行ベクトルと列ベクトルを区別しないであれば、以下の二つベクトルも等しいです。
\begin{pmatrix}1\\2\end{pmatrix}=(1,2)
大きさと向き
ベクトル$u$の大きさは$||{u}||$で表され、その向きは角度で表すことができます。

大きさと角度の計算は内積で紹介します。
ベクトルの大きさと角度で以下の定義があります:
- 平行:方向が同じまたは逆の2つのベクトルは「平行」と呼ばれ、つまり、2つのベクトルの角度が$0$または$\pi$であることを意味します。
- 直交:互いに垂直な2つのベクトルは「直交」と呼ばれ、つまり、2つのベクトルの角度が$\frac{\pi}{2}$であることを意味します。
- 単位ベクトル:長さが1のベクトルは「単位ベクトル」と呼ばれます。
零ベクトル
$n$次元ベクトルでの成分が全て$0$であれば、このベクトルが零ベクトルです。例えば、
\text{2 次元ベクトル}:\boldsymbol{0}=\begin{pmatrix}0\\0\end{pmatrix},\qquad \text{3 次元ベクトル}:\boldsymbol{0}=\begin{pmatrix}0\\0\\0\end{pmatrix}
上記の二つベクトルの幾何学的な意味は、平面及び立体空間での原点、或は始点と終点が同じな有向線分です。

零ベクトルは特殊なベクトルであり、以下の性質があります。
- 大きさ:零ベクトルの大きさが$0$です。
- 向き:零ベクトルが任意の方向に向きます。
- 角度:零ベクトルが任意の方向に向きますので、他のベクトルとの角度も任意の角度です。
- 平行と直交:角度が任意であるため、零ベクトルは任意のベクトルと平行または直交します。
ベクトルの加算
$n$次元ベクトルに対して:
\boldsymbol{a}= \begin{pmatrix}a_1\\a_2\\\vdots\\a_n\end{pmatrix},\quad \boldsymbol{b}=\begin{pmatrix}b_1\\b_2\\\vdots\\b_n\end{pmatrix}
$a$と$b$の加算、即ちベクトル加算の定義:
\boldsymbol{a}+\boldsymbol{b}
=\begin{pmatrix}a_1\\a_2\\\vdots\\a_n\end{pmatrix}
+\begin{pmatrix}b_1\\b_2\\\vdots\\b_n\end{pmatrix}=\begin{pmatrix}a_1+b_1\\a_2+b_2\\\vdots\\a_n+b_n\end{pmatrix}
加算のイメージは以下の通りです。

複数個のベクトルの加算をする際に、以下のような三角形に繋いで計算しやすくなります。

$u$と$v$の加算をする際に、$v$を平行移動して、$v$の始点を$u$の終点と接続するような形にして、$v$の終点の位置が二つベクトルの加算結果(赤い線)になります。最終的に$u$、$v$、$u+v$ が三角形になります。
\boldsymbol{u}+\boldsymbol{v}= \begin{pmatrix}3\\-2\end{pmatrix}+ \begin{pmatrix}2\\3\end{pmatrix}=\begin{pmatrix}3+2\\-2+3\end{pmatrix}=\begin{pmatrix}5\\1\end{pmatrix}
$u$を上に平行移動して、$u$の始点を$v$の終点と繋いでも同じ結果になります。
複数個のベクトルの加算でも、上記の方法を利用できます。例えば、$\boldsymbol{u}+\boldsymbol{v}+\boldsymbol{w}$

ベクトルのスカラー倍
線型代数学では、ベクトル空間のベクトルに対比するものとしての実数をスカラー(英: scalar)と呼び、ベクトルを定数倍して別のベクトルを作り出す演算としてスカラー倍が定義される。
$n$次元ベクトルに対して:
\boldsymbol{a}= \begin{pmatrix}a_1\\a_2\\\vdots\\a_n\end{pmatrix}
$a$のスカラー倍の定義:
k\boldsymbol{a}=k\begin{pmatrix}a_1\\a_2\\...\\a_n\end{pmatrix}=\begin{pmatrix}ka_1\\ka_2\\...\\ka_n\end{pmatrix},\quad k\in\mathbb{R}
例えば、$u$をスカラー倍$ku$にして、該当ベクトルの各成分$u_1$と$u_2$とも$k$倍になりました。
\boldsymbol{u}=\begin{pmatrix}u_1\\u_2\end{pmatrix}
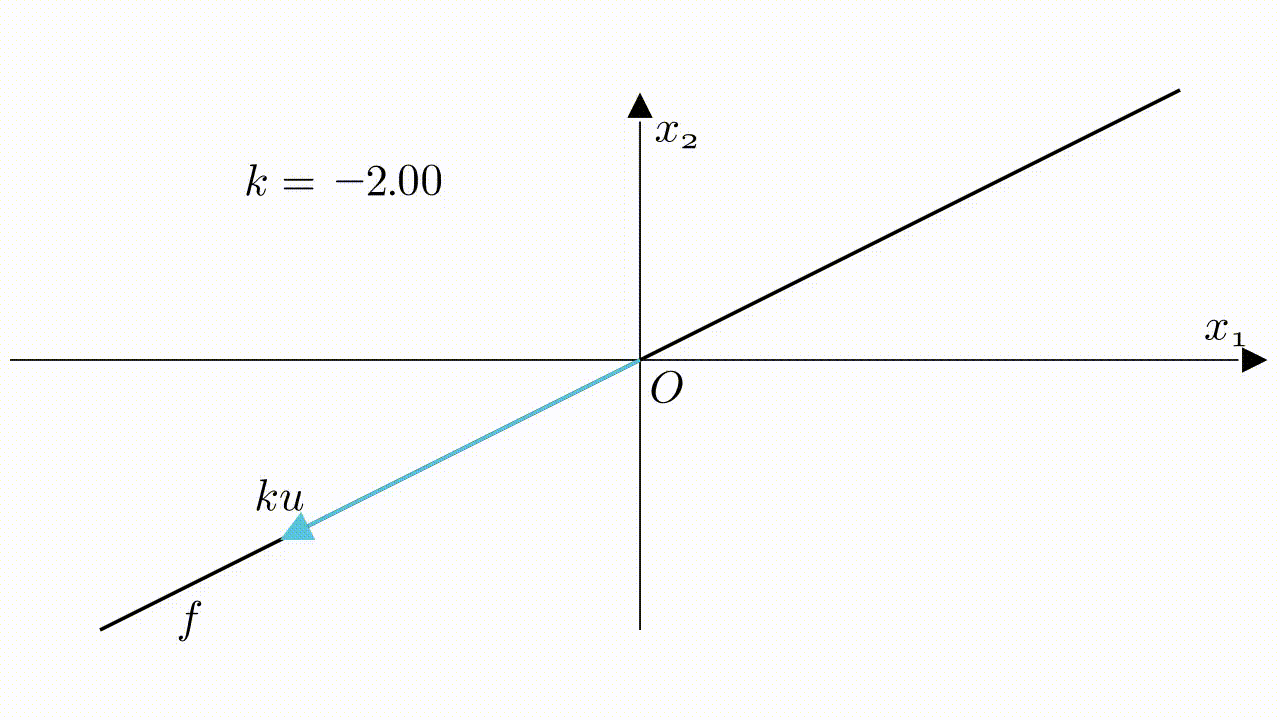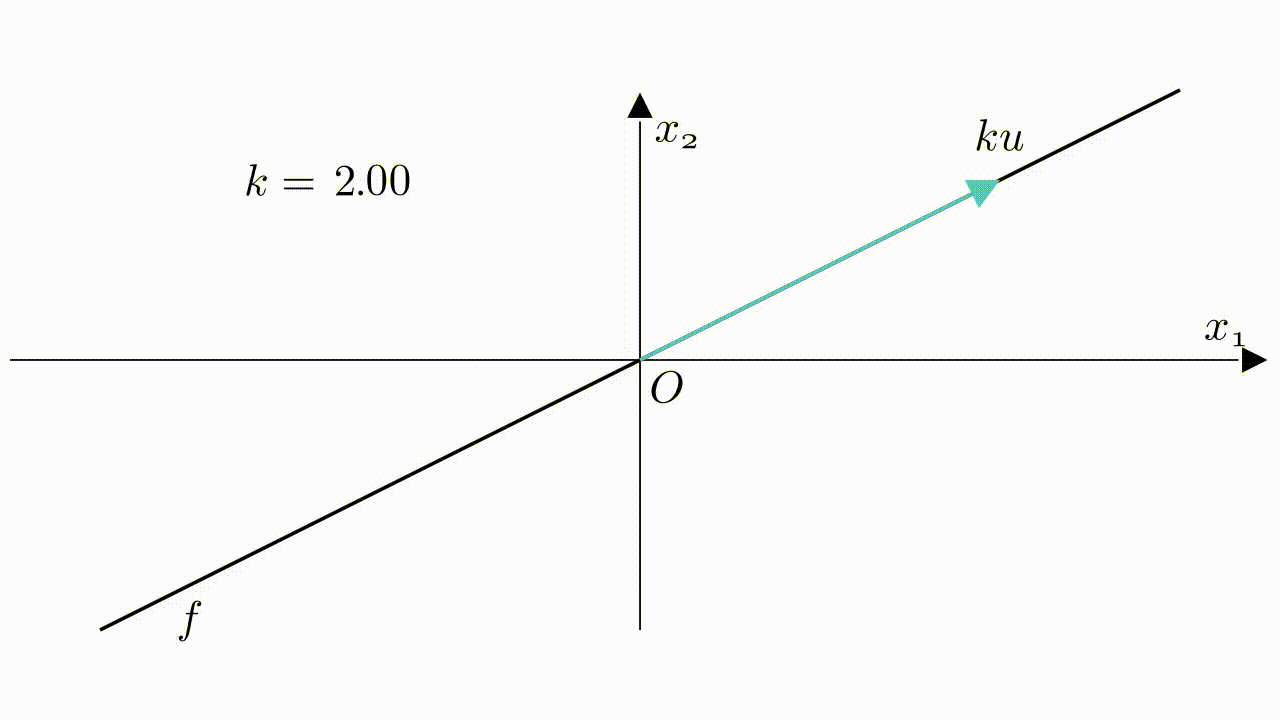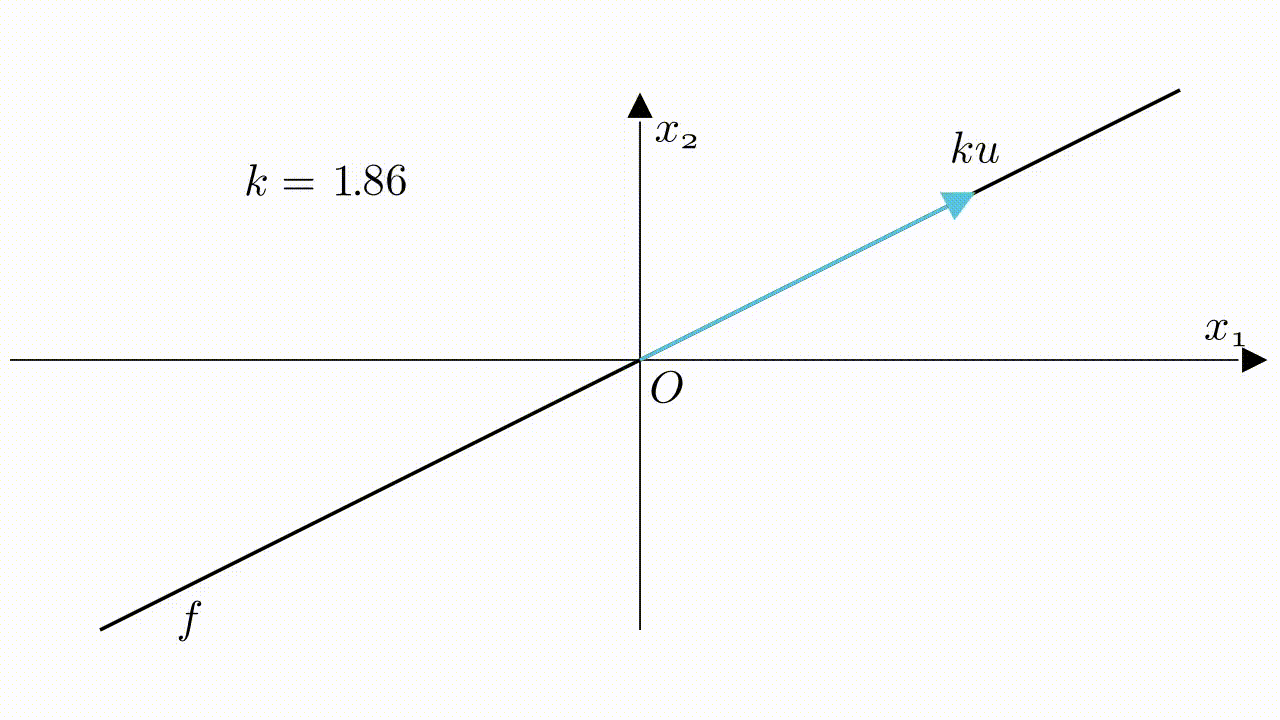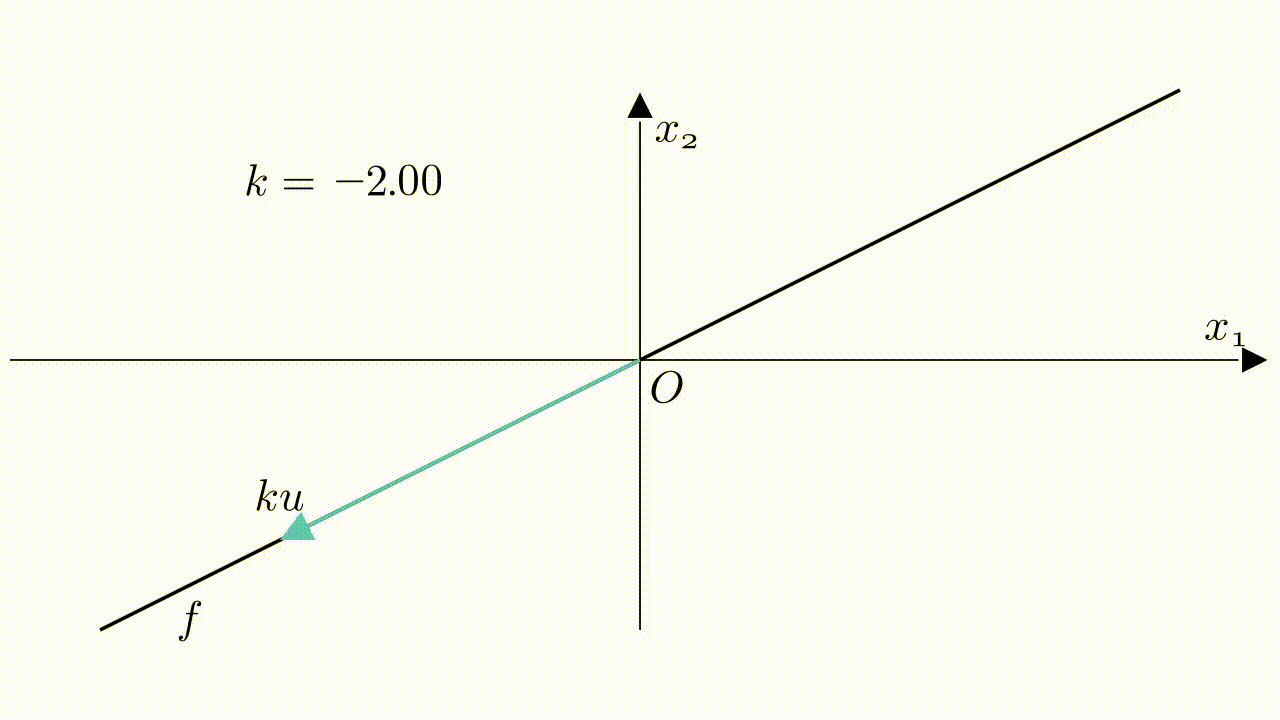
$ku$の幾何的な意味は$u$を伸ばすことです。$k$が$>0$か$<0$か、及び $k$の大きさ が伸ばす方向及び長さを決めます。

平行
伸ばしたベクトル$ku$は、元のベクトル$u$と平行します。
$\boldsymbol{u}$ と $\boldsymbol{v}$が以下の条件に満たせば、$\boldsymbol{u}$ が $\boldsymbol{v}$と平行しています:$\boldsymbol{u}\ // \ \boldsymbol{v}$
\boldsymbol{u}=k\boldsymbol{v},k\in \mathbb{R}
零ベクトルは任意のベクトルと平行します。
スカラー倍と直線
ベクトル$\boldsymbol{u}$がスカラー倍にしたら、$\boldsymbol{ku}$に変わります。$k$が実数($R$)内で変動したら、$\boldsymbol{ku}$が直線での全ての点を表すことができます。
直線$f$がスカラー倍の形で表せます。
f=k\boldsymbol{u},\quad k\in\mathbb{R}
減算の幾何的意味
減算は、以下のように加算とスカラー倍の組み合わせで、計算できます。
\boldsymbol{u}+(\boldsymbol{-u})=\boldsymbol{u}-\boldsymbol{u}=\begin{pmatrix}u_1\\u_2\\\vdots\\u_n\end{pmatrix}+\begin{pmatrix}-u_1\\-u_2\\\vdots\\-u_n\end{pmatrix}=\begin{pmatrix}0\\0\\\vdots\\0\end{pmatrix}
参考情報