材料の特性(応力と歪の関係)が弾性域では比例(線形)しているため、構造解析の解は、容易に求める事ができます。
しかし、塑性域に入ると、応力と歪の関係が線形ではなく、非線形となるため、解を求める事が難しくなってきます。
求め方は、負荷を一度に掛けず少しづつ掛けてその都度、解を求め、最終的に解を求める方法で解きます。
したがって、あまりに大きな負荷を掛け過ぎると、途中の解が収束せず求められなくなります。
この場合は、さらに時間をかけて少しづつ負荷を掛けていく方法となります。
この資料はオープンCAE勉強会@岐阜で公開されているFS氏ご提供の「SALOME-Mecaの使用法解説:7.0 塑性変形の基本(1),(2)」をSalome-Meca 2018(Code_Aster 13.6)のAsterStudyモジュールを用いて実行しました。
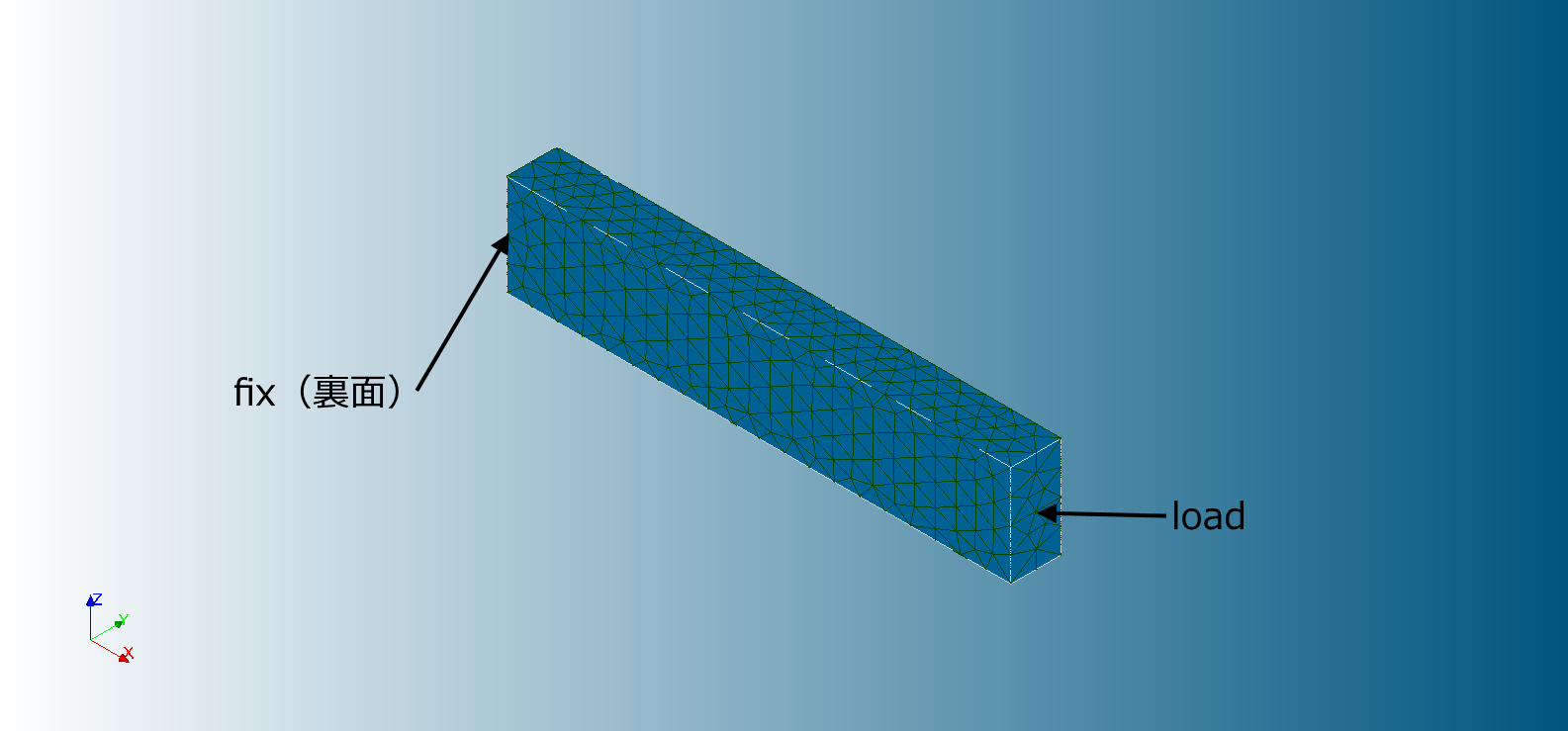
単純な四角柱の片持ち梁
ジオメトリ
幅10mm×高さ20mm×長さ100mmの直方体
材料
- ヤング率:E=70,000MPa
- ポアソン比:$\nu$=0.3
- Stress Strain Curve Data
| Stress | Strain |
|---|---|
| 105.0 | 0.0015 |
| 200.0 | 0.0500 |
| 300.0 | 0.2000 |
拘束条件と荷重条件
| 境界条件 | トポロジ | 境界条件の種類 | 条件 |
|---|---|---|---|
| fix | 面 | 変位 | DX=DY=DZ=0 |
| load | 面 | 変位 | DZ=5 |
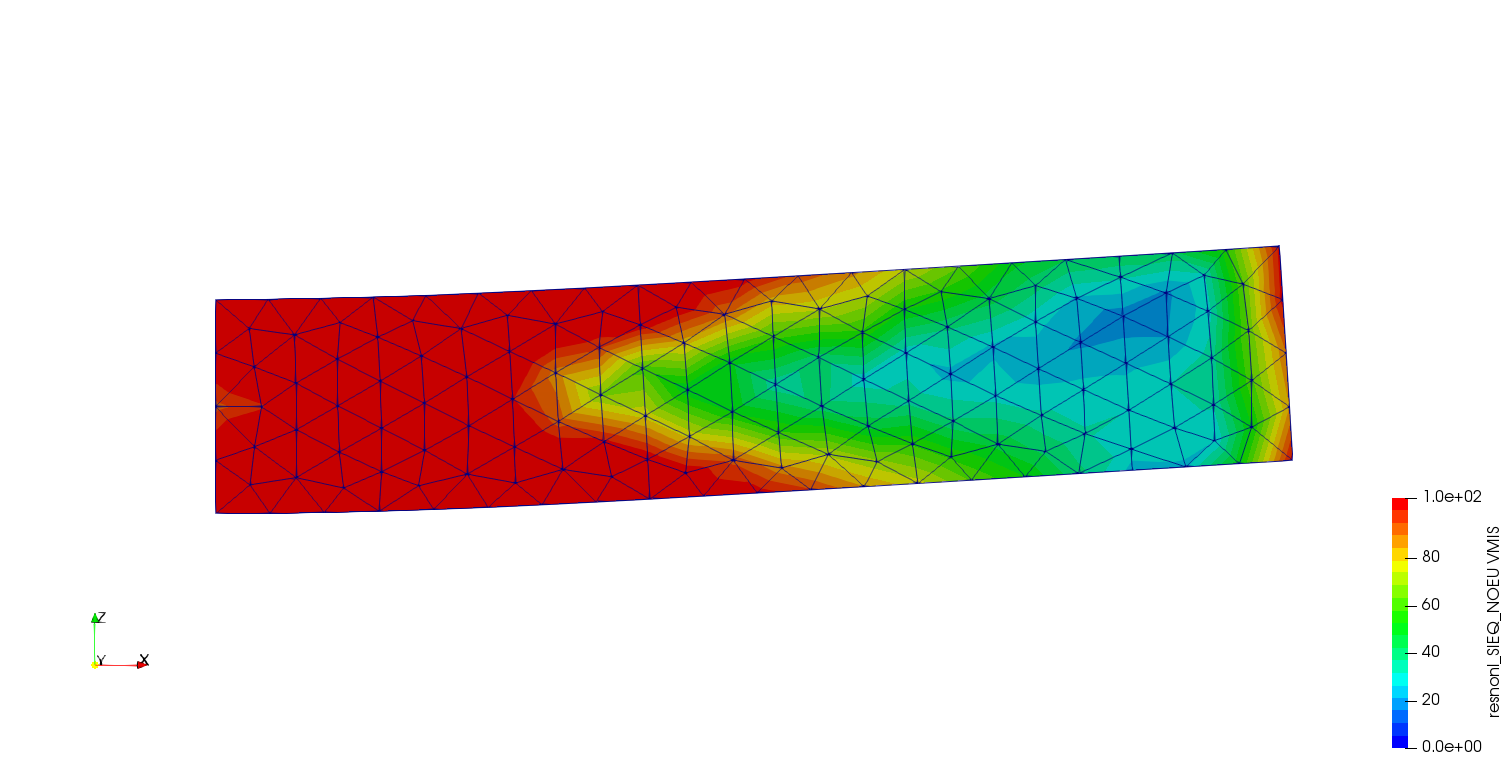
解析結果
相当応力図を示します。
コマンドファイル
DEBUT(LANG='EN')
mesh = LIRE_MAILLAGE(FORMAT='MED',
UNITE=20)
model = AFFE_MODELE(AFFE=_F(MODELISATION=('3D', ),
PHENOMENE='MECANIQUE',
TOUT='OUI'),
MAILLAGE=mesh)
elast_pl = DEFI_FONCTION(INTERPOL=('LIN', ),
NOM_PARA='EPSI',
NOM_RESU='TOUTRESU',
PROL_DROITE='LINEAIRE',
PROL_GAUCHE='CONSTANT',
VALE=(0.0015, 105.0, 0.05, 200.0, 0.2, 300.0))
mater = DEFI_MATERIAU(ELAS=_F(E=70000.0,
NU=0.3),
TRACTION=_F(SIGM=elast_pl))
fieldmat = AFFE_MATERIAU(AFFE=_F(MATER=(mater, ),
TOUT='OUI'),
MAILLAGE=mesh)
depl_imp = DEFI_FONCTION(NOM_PARA='INST',
VALE=(0.0, 0.0, 1.0, 1.0))
listr = DEFI_LIST_REEL(DEBUT=0.0,
INTERVALLE=_F(JUSQU_A=1.0,
PAS=0.1))
times = DEFI_LIST_INST(DEFI_LIST=_F(LIST_INST=listr),
METHODE='MANUEL')
load = AFFE_CHAR_MECA(DDL_IMPO=_F(DZ=5.0,
GROUP_MA=('load', )),
MODELE=model)
fix = AFFE_CHAR_MECA(DDL_IMPO=_F(DX=0.0,
DY=0.0,
DZ=0.0,
GROUP_MA=('fix', )),
MODELE=model)
resnonl = STAT_NON_LINE(CHAM_MATER=fieldmat,
COMPORTEMENT=_F(DEFORMATION='SIMO_MIEHE',
RELATION='VMIS_ISOT_TRAC'),
CONVERGENCE=_F(ITER_GLOB_MAXI=200,
RESI_GLOB_MAXI=1e-06),
EXCIT=(_F(CHARGE=fix),
_F(CHARGE=load,
FONC_MULT=depl_imp)),
INCREMENT=_F(LIST_INST=listr),
METHODE='NEWTON',
MODELE=model,
NEWTON=_F(MATRICE='TANGENTE',
REAC_INCR=1,
REAC_ITER=1))
resnonl = CALC_CHAMP(reuse=resnonl,
CONTRAINTE=('SIGM_ELNO', 'SIGM_NOEU'),
CRITERES=('SIEQ_ELNO', 'SIEQ_NOEU', 'EPEQ_ELNO', 'EPEQ_NOEU'),
DEFORMATION=('EPSP_ELNO', 'EPSP_NOEU'),
FORCE=('FORC_NODA', 'REAC_NODA'),
MODELE=model,
RESULTAT=resnonl,
TOUT='OUI')
IMPR_RESU(FORMAT='MED',
RESU=_F(MAILLAGE=mesh,
RESULTAT=resnonl,
TOUT_CHAM='OUI'),
UNITE=80)
FIN()
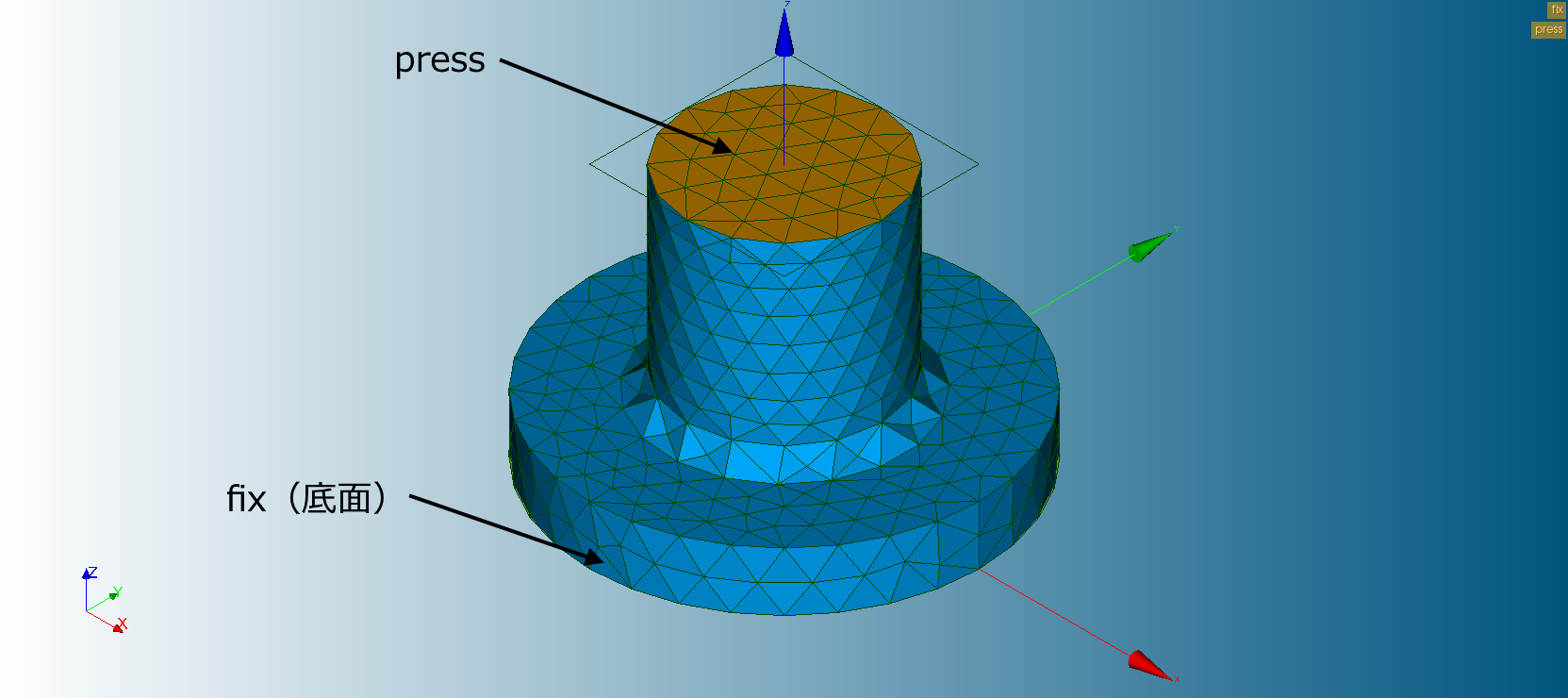
円柱の圧縮
塑性加工として、かしめ加工がありますが、このかしめを想定したモデルで塑性解析を実施します。
モデルは、円盤の上に、円柱が立っているモデルで円柱を圧縮して、円柱の形状がどのように変化するかを確認します。
(通常円柱を圧縮すると、たいこ形状になります。
円柱の端面に荷重を掛けるので、端面は、摩擦により、ほとんど伸びません。
円柱の中央付近は、圧縮により膨らんで、たいこ形状になります。)
ジオメトリ
- 円柱外形:$\phi$10mm
- 円柱高さ:10mm
- つなぎR:R1mm
- 円盤外形:$\phi$20mm
- 円盤板厚:t3mm
材料
- ヤング率:E=70,000MPa
- ポアソン比:$\nu$=0.3
- Stress Strain Curve Data
| Stress | Strain |
|---|---|
| 105.0 | 0.0015 |
| 200.0 | 0.0500 |
| 300.0 | 0.2000 |
拘束条件と荷重条件
| 境界条件 | トポロジ | 境界条件の種類 | 条件 |
|---|---|---|---|
| fix | 面 | 変位 | DX=DY=DZ=0 |
| press | 面 | 変位 | DX=DY=0 DZ=-3 |
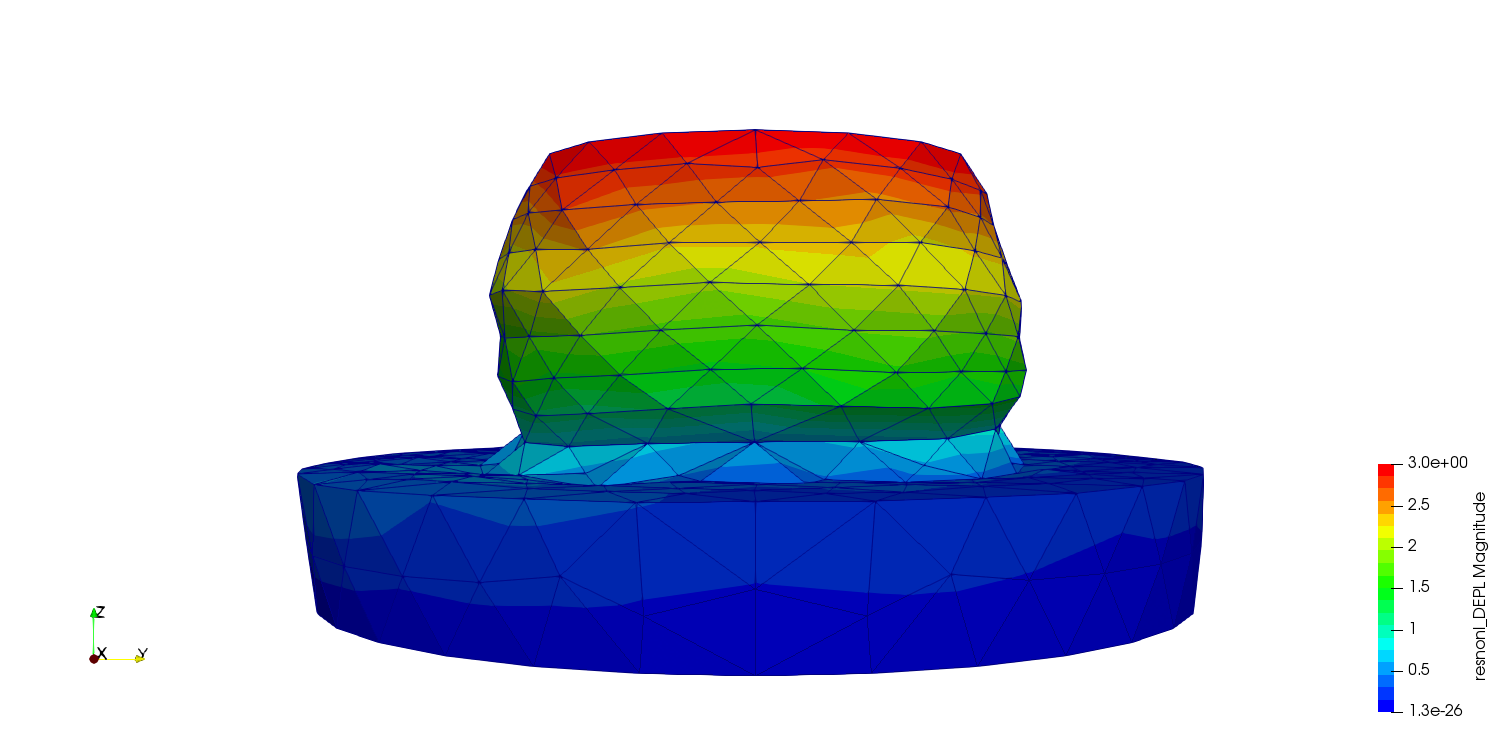
解析結果
変形図を示します。
コマンドファイル
DEBUT(LANG='EN')
mesh = LIRE_MAILLAGE(FORMAT='MED',
UNITE=20)
model = AFFE_MODELE(AFFE=_F(MODELISATION=('3D', ),
PHENOMENE='MECANIQUE',
TOUT='OUI'),
MAILLAGE=mesh)
elast_pl = DEFI_FONCTION(INTERPOL=('LIN', ),
NOM_PARA='EPSI',
NOM_RESU='TOUTRESU',
PROL_DROITE='LINEAIRE',
PROL_GAUCHE='CONSTANT',
VALE=(0.0015, 105.0, 0.05, 200.0, 0.2, 300.0, 2.0, 3000.0))
mater = DEFI_MATERIAU(ELAS=_F(E=70000.0,
NU=0.3),
TRACTION=_F(SIGM=elast_pl))
fieldmat = AFFE_MATERIAU(AFFE=_F(MATER=(mater, ),
TOUT='OUI'),
MAILLAGE=mesh)
depl_imp = DEFI_FONCTION(NOM_PARA='INST',
VALE=(0.0, 0.0, 1.0, 1.0))
listr = DEFI_LIST_REEL(DEBUT=0.0,
INTERVALLE=(_F(JUSQU_A=0.1,
NOMBRE=5),
_F(JUSQU_A=1.0,
NOMBRE=5)))
times = DEFI_LIST_INST(DEFI_LIST=_F(LIST_INST=listr),
METHODE='MANUEL')
load = AFFE_CHAR_MECA(DDL_IMPO=_F(DZ=-3.0,
GROUP_MA=('press', )),
MODELE=model)
fix = AFFE_CHAR_MECA(DDL_IMPO=(_F(DX=0.0,
DY=0.0,
DZ=0.0,
GROUP_MA=('fix', )),
_F(DX=0.0,
DY=0.0,
GROUP_MA=('press', ))),
MODELE=model)
resnonl = STAT_NON_LINE(CHAM_MATER=fieldmat,
COMPORTEMENT=_F(DEFORMATION='SIMO_MIEHE',
RELATION='VMIS_ISOT_TRAC'),
CONVERGENCE=_F(ITER_GLOB_MAXI=200,
RESI_GLOB_MAXI=1e-06),
EXCIT=(_F(CHARGE=fix),
_F(CHARGE=load,
FONC_MULT=depl_imp)),
INCREMENT=_F(LIST_INST=listr),
METHODE='NEWTON',
MODELE=model,
NEWTON=_F(MATRICE='TANGENTE',
REAC_INCR=1,
REAC_ITER=1))
resnonl = CALC_CHAMP(reuse=resnonl,
CONTRAINTE=('SIGM_ELNO', 'SIGM_NOEU'),
CRITERES=('SIEQ_ELNO', 'SIEQ_NOEU', 'EPEQ_ELNO', 'EPEQ_NOEU'),
DEFORMATION=('EPSP_ELNO', 'EPSP_NOEU'),
FORCE=('FORC_NODA', 'REAC_NODA'),
MODELE=model,
RESULTAT=resnonl,
TOUT='OUI')
IMPR_RESU(FORMAT='MED',
RESU=_F(MAILLAGE=mesh,
RESULTAT=resnonl,
TOUT_CHAM='OUI'),
UNITE=80)
FIN()