構造物を設計する場合、構造物の固有振動数がどこにあるのか、また、その周波数で強振した場合、どのような形状で強振しているのかが、問題になることがあります。
強振して構造物が破壊した場合、これらの事がわかれば、対策がとれます。
このため、ここで固有振動数と変形の形状を解析する方法(モーダル解析)を示します。
この資料はオープンCAE勉強会@岐阜で公開されているFS氏ご提供の「SALOME-Mecaの使用法解説:10.0モーダル解析」をSalome-Meca 2018(Code_Aster 13.6)のAsterStudyモジュールを用いて実行しました。
ジオメトリ
幅10mm×高さ20mm×長さ100mmの直方体
材料
- ヤング率:E=132,000MPa
- ポアソン比:$\nu$=0.343
- 密度:$\rho$=8.96e-9 Ton/mm3
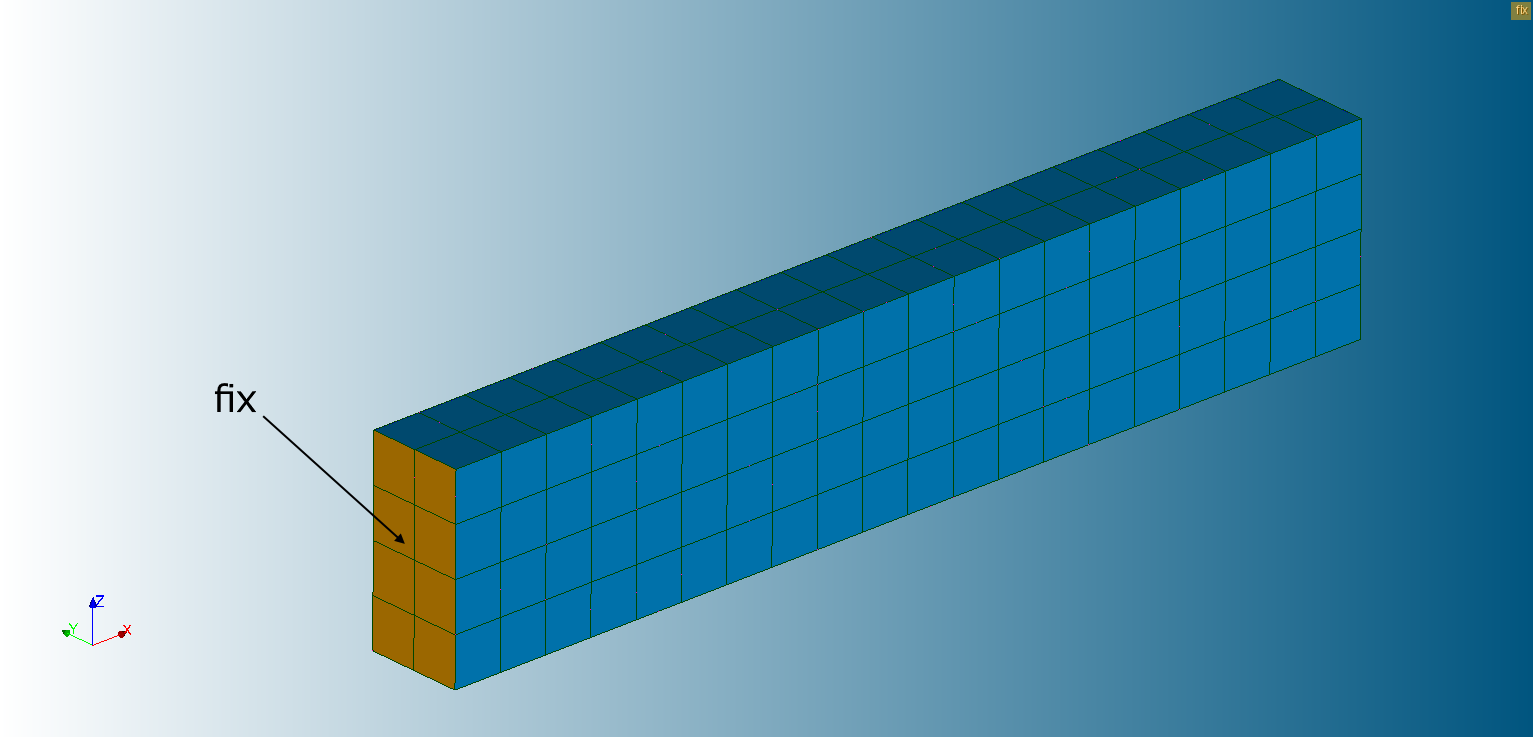
拘束条件と荷重条件
| 境界条件 | トポロジ | 境界条件の種類 | 条件 |
|---|---|---|---|
| fix | 面 | 変位 | DX=DY=DZ=0 |
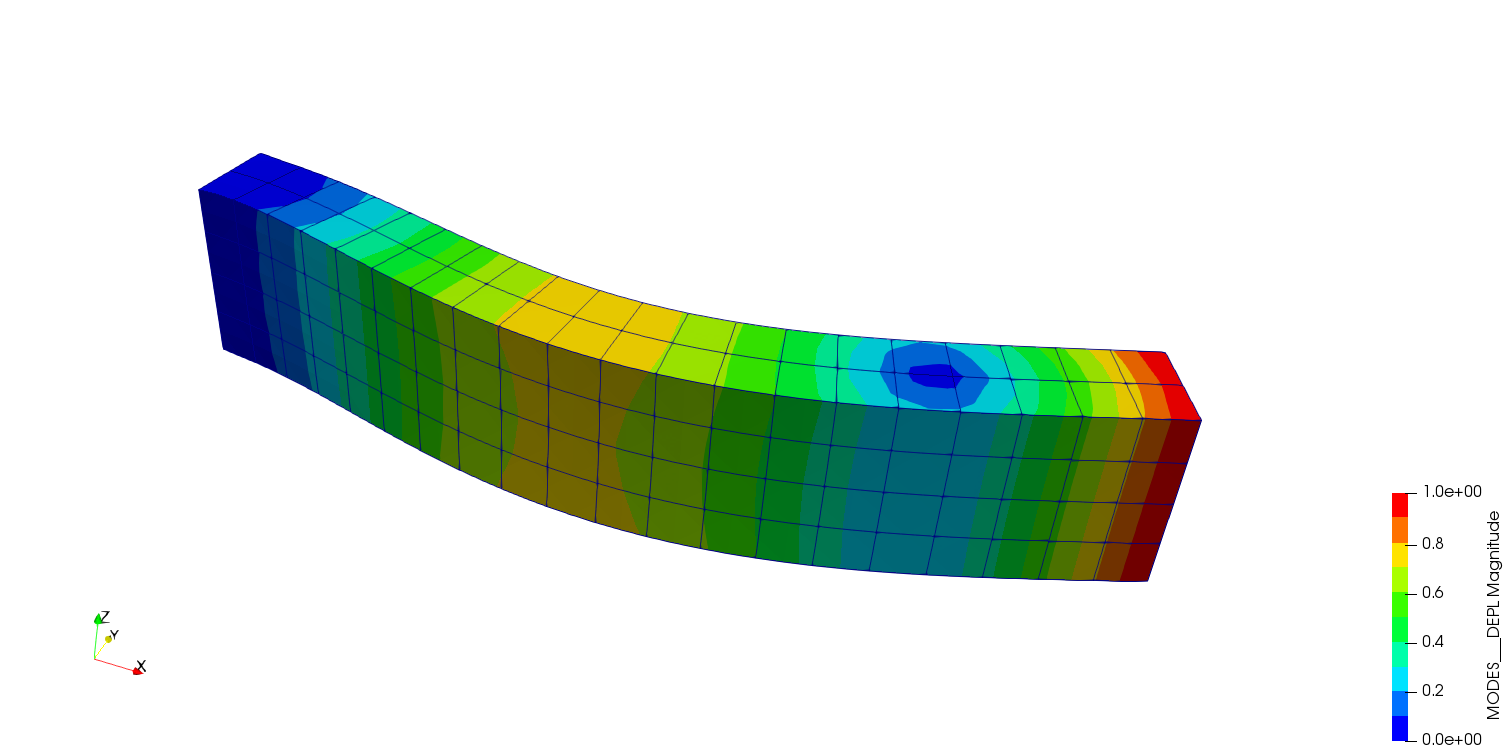
解析結果
六面体1次要素、メッシュサイズ5mm、3次の変形図(×10倍表示)を示します。
結果を理論解と比較してみます。
理論計算とCAE解析結果を比較すると、次表のようになります。
| 区分 | 1次 | 2次 | 3次 |
|---|---|---|---|
| CAE解析結果 | 624 | 1,214 | 3,739 |
| 理論解 | 622 | 1,242 | 3,885 |
コマンドファイル
bar100.comm
DEBUT(LANG='EN')
MAIL = LIRE_MAILLAGE(FORMAT='MED',
UNITE=20)
MODEL = AFFE_MODELE(AFFE=_F(MODELISATION=('3D', ),
PHENOMENE='MECANIQUE',
TOUT='OUI'),
MAILLAGE=MAIL)
Cu = DEFI_MATERIAU(ELAS=_F(E=132000.0,
NU=0.343,
RHO=8.96e-09))
CHMAT = AFFE_MATERIAU(AFFE=_F(MATER=(Cu, ),
TOUT='OUI'),
MAILLAGE=MAIL,
MODELE=MODEL)
BLOCAGE = AFFE_CHAR_MECA(DDL_IMPO=_F(DX=0.0,
DY=0.0,
DZ=0.0,
GROUP_MA=('fix', )),
MODELE=MODEL)
ASSEMBLAGE(CHAM_MATER=CHMAT,
CHARGE=(BLOCAGE, ),
MATR_ASSE=(_F(MATRICE=CO('MASSE'),
OPTION='MASS_MECA'),
_F(MATRICE=CO('RIGIDITE'),
OPTION='RIGI_MECA')),
MODELE=MODEL,
NUME_DDL=CO('NUMDDL'))
MODES = CALC_MODES(CALC_FREQ=_F(NMAX_FREQ=5),
MATR_MASS=MASSE,
MATR_RIGI=RIGIDITE,
OPTION='PLUS_PETITE')
MODES = CALC_CHAMP(reuse=MODES,
CONTRAINTE=('SIEF_ELGA', ),
RESULTAT=MODES)
IMPR_RESU(FORMAT='MED',
RESU=_F(MAILLAGE=MAIL,
RESULTAT=MODES),
UNITE=80)
FIN()