Salome-Meca 2018を用いた線形熱応力解析（SSLV）

静的に熱応力を計算します。
温度は均一に分布しているものとして、線形の弾性解析を行います。

この資料はオープンCAE勉強会＠岐阜で公開されているFS氏ご提供の「SALOME-Mecaの使用法解説：5.0 線形熱応力(1)、5.1 線形熱応力(2)」をSalome-Meca 2018（Code_Aster 13.6）のAsterStudyモジュールを用いて実行しました。

ジオメトリ

幅10mm×高さ20mm×長さ100mmの直方体

材料

• ヤング率：E=70,600MPa
• ポアソン比：$\nu$=0.345
• 線膨張係数：$\alpha$=2.3e-5

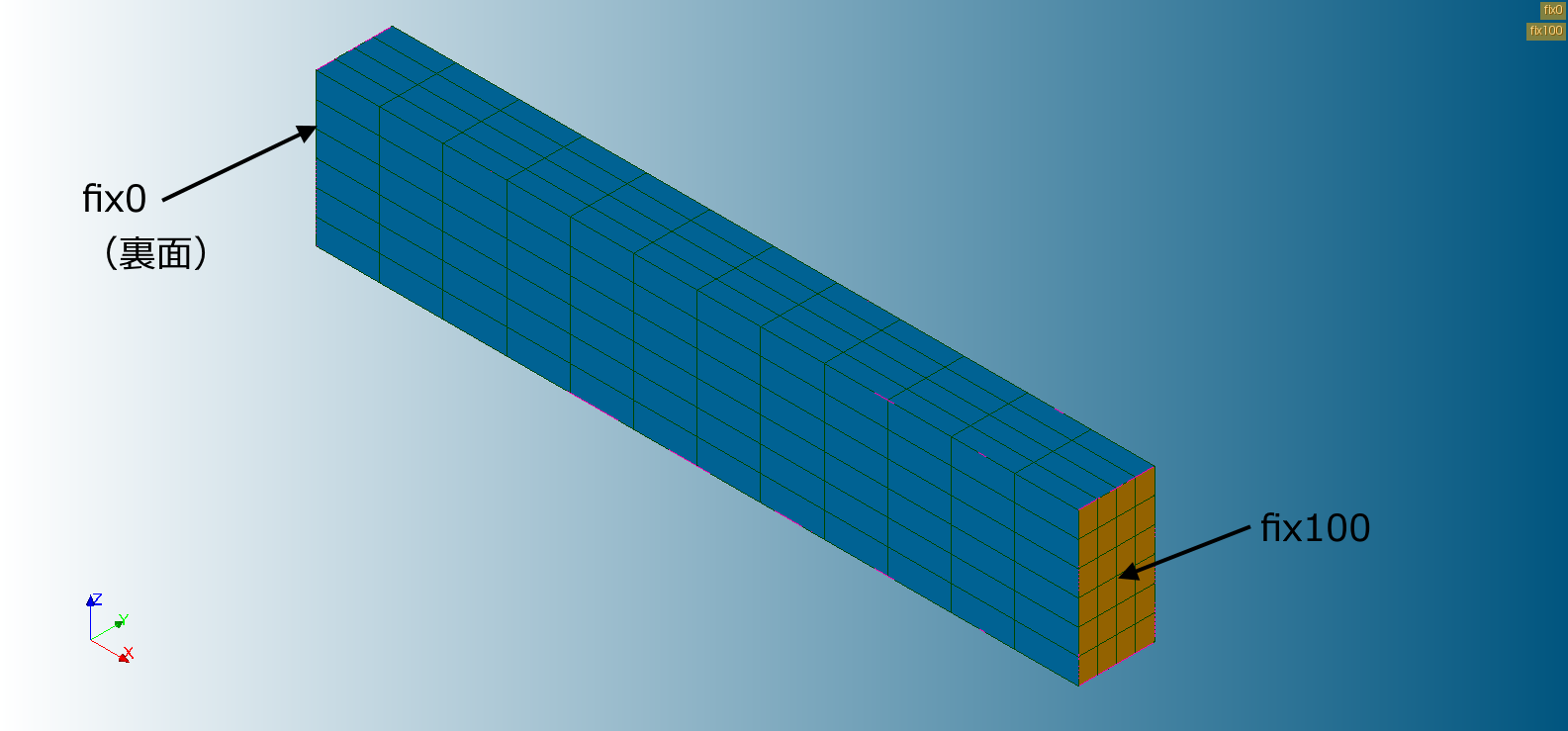
拘束条件と荷重条件

20℃から120℃の温度変化を与えます。

境界条件	トポロジ	境界条件の種類	条件
fix0 fix100	面	変位	DX=DY=DZ=0

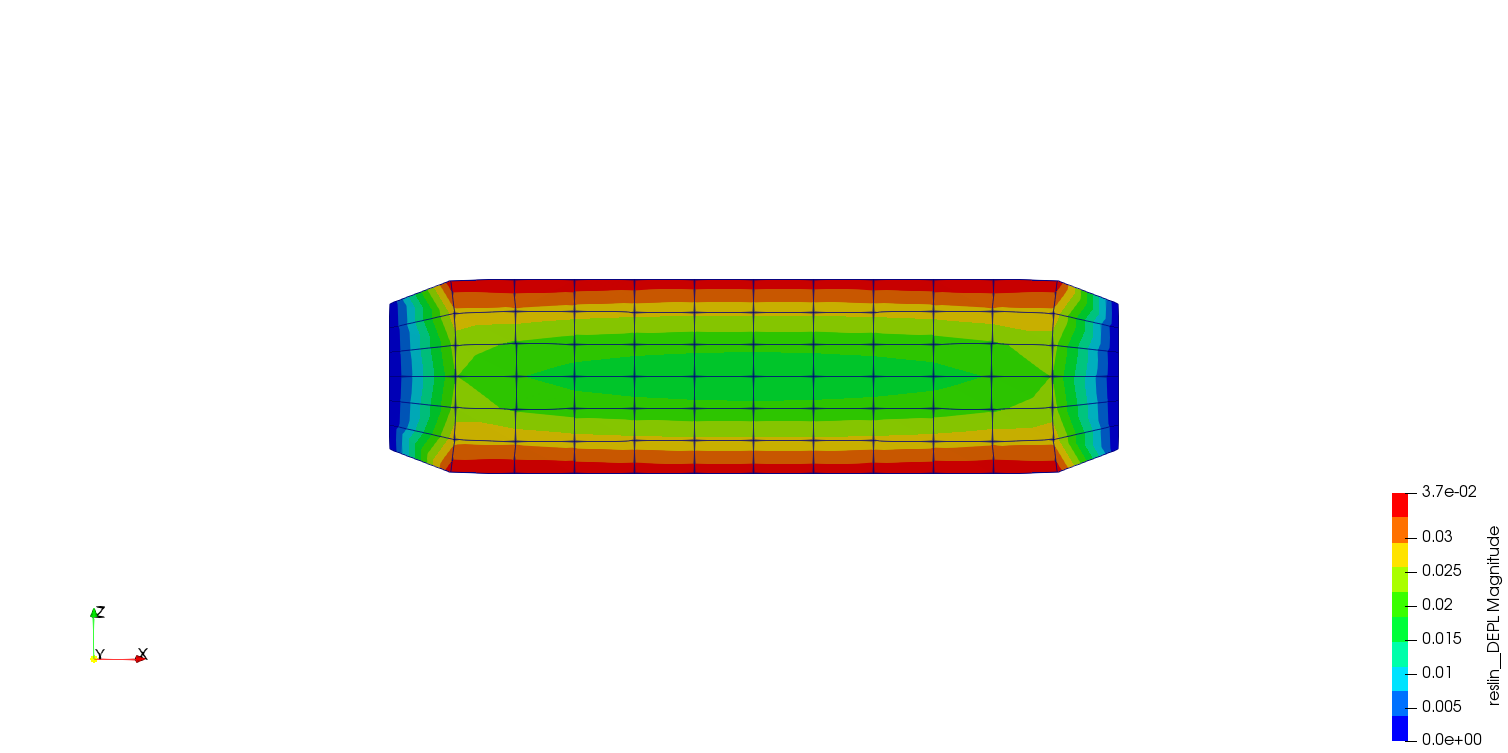
解析結果

変形図（×100倍表示）を示します。

コマンドファイル

bar-true.comm

DEBUT(LANG='EN')

mesh = LIRE_MAILLAGE(FORMAT='MED',
                     UNITE=20)

mesh = MODI_MAILLAGE(reuse=mesh,
                     MAILLAGE=mesh,
                     ORIE_PEAU_3D=_F(GROUP_MA=('fix100', 'fix0')))

model = AFFE_MODELE(AFFE=_F(MODELISATION=('3D', ),
                            PHENOMENE='MECANIQUE',
                            TOUT='OUI'),
                    MAILLAGE=mesh)

Aluminum = DEFI_MATERIAU(ELAS=_F(ALPHA=2.3e-05,
                                 E=70600.0,
                                 NU=0.345))

load = AFFE_CHAR_MECA(DDL_IMPO=_F(DX=0.0,
                                  DY=0.0,
                                  DZ=0.0,
                                  GROUP_MA=('fix100', 'fix0')),
                      MODELE=model)

tempS = CREA_CHAMP(AFFE=_F(NOM_CMP=('TEMP', ),
                           TOUT='OUI',
                           VALE=(120.0, )),
                   MODELE=model,
                   OPERATION='AFFE',
                   TYPE_CHAM='NOEU_TEMP_R')

fieldmat = AFFE_MATERIAU(AFFE=_F(MATER=(Aluminum, ),
                                 TOUT='OUI'),
                         AFFE_VARC=_F(CHAM_GD=tempS,
                                      NOM_VARC='TEMP',
                                      TOUT='OUI',
                                      VALE_REF=20.0),
                         MAILLAGE=mesh)

reslin = MECA_STATIQUE(CHAM_MATER=fieldmat,
                       EXCIT=_F(CHARGE=load),
                       MODELE=model)

reslin = CALC_CHAMP(reuse=reslin,
                    CONTRAINTE=('SIGM_ELNO', 'SIGM_NOEU'),
                    CRITERES=('SIEQ_ELNO', 'SIEQ_NOEU'),
                    RESULTAT=reslin)

IMPR_RESU(FORMAT='MED',
          RESU=_F(NOM_CHAM=('SIGM_NOEU', 'SIEQ_NOEU', 'DEPL'),
                  RESULTAT=reslin),
          UNITE=80)

FIN()