このエントリーはオープンCAE Advent Calendar 2020 の20日目です。
この資料は岐阜工業高等専門学校 柴田先生が公開された第14回オープンCAE勉強会@岐阜での発表資料「Salomeの使い方 - トルク解析」1とCAELinuxでClaus Andersen氏が投稿された記事「ApplyingTorque」2を参考に、Salome-Mea 2019用に作成しました。
操作がわかりにくいときはYouTube動画の方でもご確認ください。
Code_Asterでトルクをかける
Code_Asterには、構造体にトルクを適用するための簡単な方法がありません。
節点だけがモーメント(FORCE_NODALE $\Rightarrow$MX、MY、MZ)を適用するオプションを持っています。これは何を意味するかというと、オブジェクトにトルクを適用するためには、単一の節点をオブジェクトに接続し、それによってモーメントをトルクに変換しなければならないということです。これを実現する方法はいくつかありますが、ここではそのうちの1つだけを説明します。Code_Asterの中で何が起こるかというと、この方法では、トルクをかけたい面に隣接して単一節点を配置し、単一節点と面の間に剛体リンクを作り、最後にモーメントをかける、それによってトルクをかけることになります。
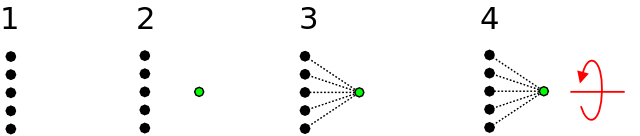
- トルクをかけたいサーフェス
- 隣接する単一節点の作成
- Code_Asterは節点と表面の間に剛性の高いリンクを作成します
- 単一節点にモーメントを適用
単一節点に力(FORCE_NODALE - FX、 FY、FZ)を適用する場合、力は各節点に等しく分配されますので、この場合、各節点は適用された力の1/5を受け取ることになります。
Salomeでのグループの作成
(ジオメトリを作成してメッシュ化することに精通している必要があります。)
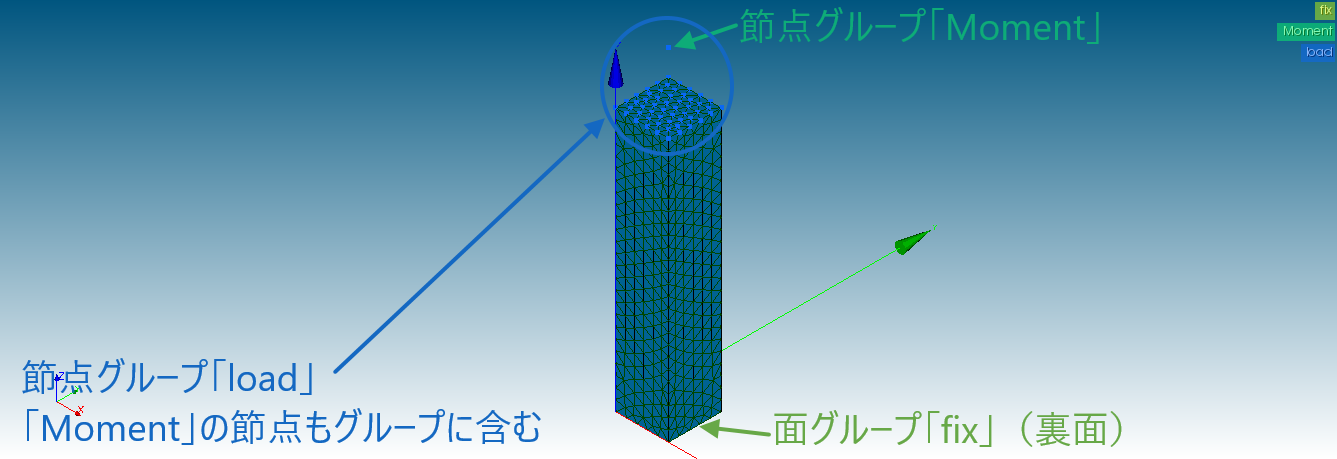
オブジェクトをメッシュ化し、トルクを適用したいサーフェスの中心と垂直な単一節点を作成します。この場合、単一節点を選択しやすいように、サーフェスに対して垂直なオフセットを使用して作成するのが理にかなっています。単一節点に「節点グループ」を割り当てます。
トルクを適用したいサーフェスは、「サーフェスグループ」ではなく「節点グループ」に割り当てる必要があります(重要)。先ほど作成した単一の節点を含めます(重要)。最後に、オブジェクトが動かないようにするサーフェスにサーフェスグループ(またはお好みのもの)を割り当てます。ここではオブジェクトの底面です。次の図を参照してください。
モデルの作成
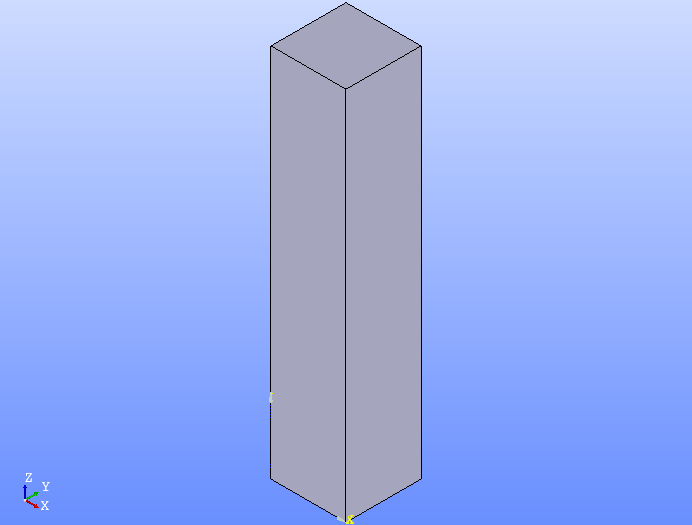
今回解析するモデルは、次の図に示す100×100×500(mm)のモデルとします。
初めに、次の図に示す部分を選択してShaperモジュールを起動します。
「Part」>「New Part」で新規パーツの作成を開始します。
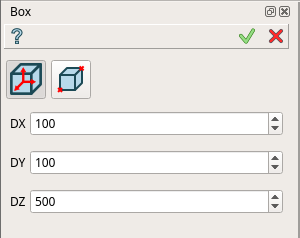
「Primitives」>「Box」を選択します。
表示されたパネル内「By dimensions」の「DX」、「DY」、「DZ」に寸法を入力します。今回は100×100×500mmなので、「DX」には"100"(mm)、「DY」には"100"(mm)、「DZ」には"500"(mm)を入力し、「Apply」を選択します。
グループの作成
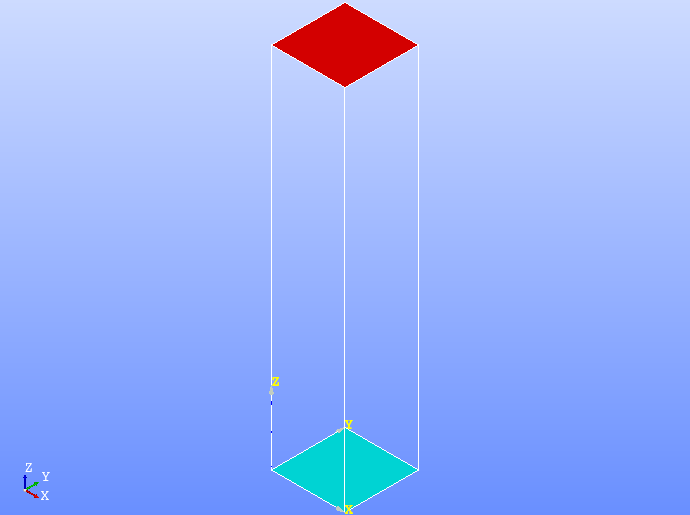
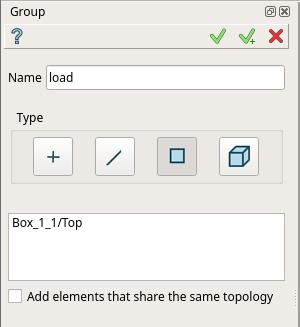
グループは、次の図に青色で示す面を固定面「fix」、赤色で示す面を荷重面「load」とします。
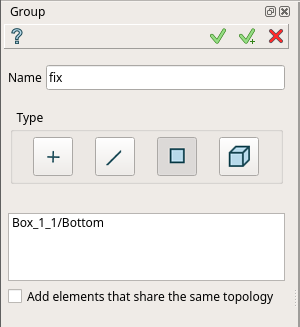
「Features」>「Group」を選択します。「Type」でグループのタイプを選択します。今回は面を指定するので、左から3番目の「Faces」を選択します。「Name」欄にグループ名を入力します。 今回は"fix"と入力します。グループを指定する面を選択します。モデルが表示されている画面で先の図に青色で示した面を選択します。選択した面の輪郭が白くなったら、ウィンドウ右上の「Apply and continue」をクリックします。また、選択しづらい場合には、キーボード「Ctrl」キーを押した状態でマウスの右ボタンをドラッグすることで、表示角度を自由に動かすことができます。「load」グループについても同様に作成します。最後に「Apply」をクリックします。
「Features」>「Export to GEOM」を選択します。これで、モデルの作成が完了しました。
メッシュ作成
初めに、次の図に示す部分を選択してMeshモジュールに変更します。
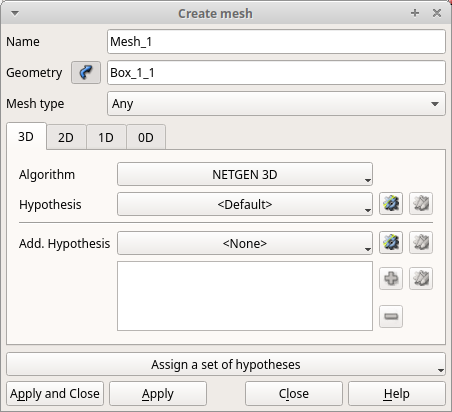
「Mesh」>「Create Mesh」を選択します。
表示されたウィンドウ内GeometryにObject Browserから「Box_1_1」を選択します。次にウィンドウ下部の「Assign a set of hypotheses」をクリックし、「3D:Automatic Tetrahedralization」を選択します。
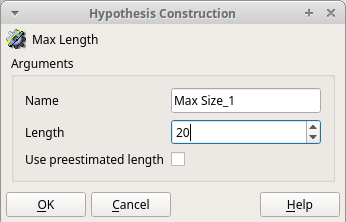
選択すると、「Hypothesis Construction」という小さなウィンドウが表示されます。このウィンドウ内の「Length」で、メッシュ長さを設定します。今回はメッシュ長さを20mmとするので、「Length」の欄に"20"(mm)と入力し、「OK」を選択します。
ここで元のメッシュウィンドウに戻るので「Apply and Close」を選択します。 Object Browser内に、さきほど作成した「Mesh_1」が表示されるので、「Mesh_1」を選択し、右クリックをして「Compute」を選択します。
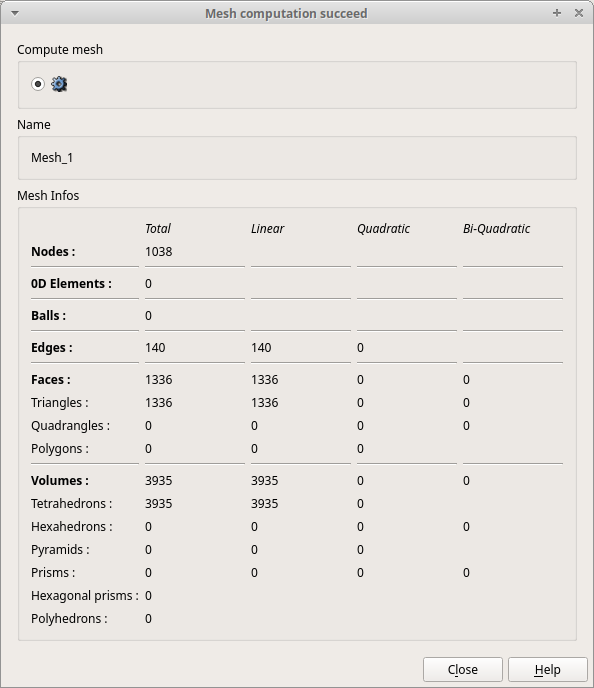
メッシュ作成が完了すると、「Mesh computation succeed」というウィンドウが表示されます。
ここでメッシュの要素数等を確認することができます。
これで、メッシュの作成が完了しました。
荷重点の作成
モーメントを作用させる点を作成します。
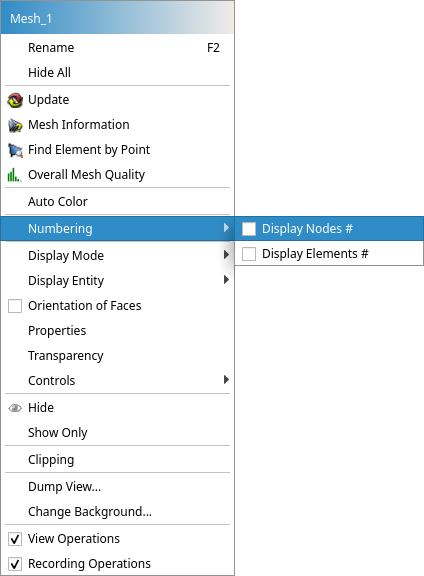
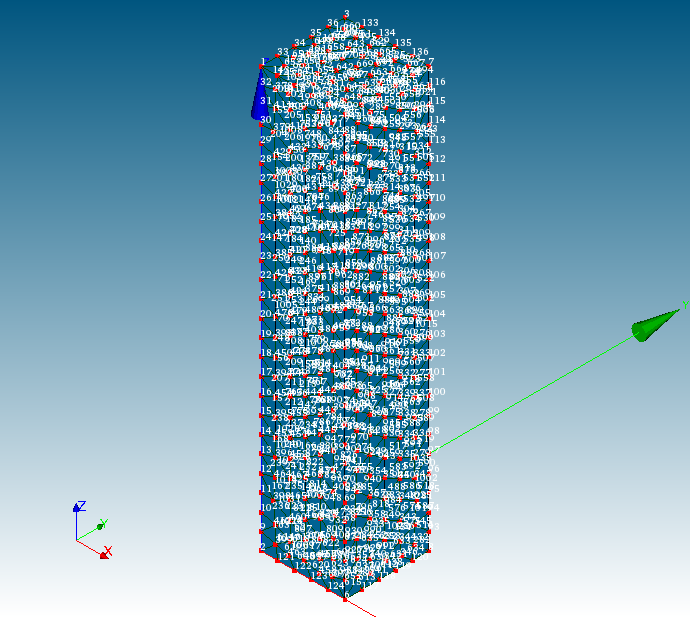
まず、Object Browser内の「Mesh_1」を選択した状態で、モデルが表示されている画面で右クリックをし、「Numbering」>「Display Node #」を選択します。
すると、各点に番号が表示されます。
「Modification」>「Add」>「Node」を選択します。
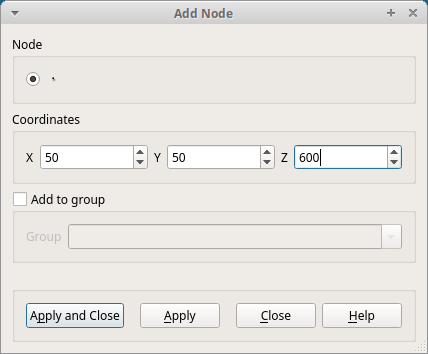
表示されたウィンドウ内「Coordinates」に、作成する点の座標を入力します。
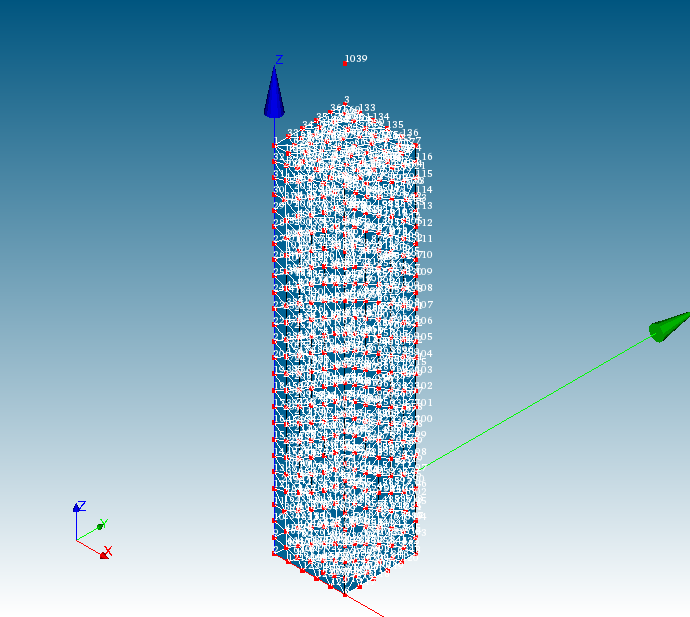
今回は「X」に"50"(mm)、「Y」に"50"(mm)、「Z」に"600"(mm)を入力し、Object Browser内「Mesh_1」を選択した状態で「Apply and Close」をクリックします。すると、モデルが表示されている画面に「1039」という点番号が表示されます。
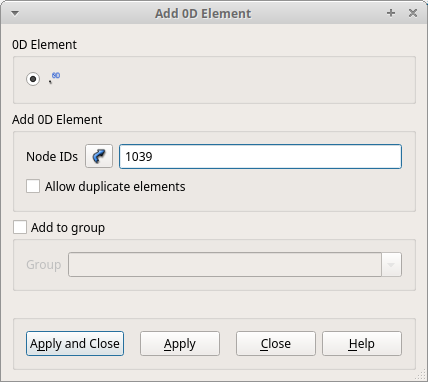
「Modification」>「Add」>「0D Element」を選択します。
表示されたウィンドウ内「Add 0D Element」の「Nodes IDs」に、さきほど表示された点番号"1039"を入力し、Object Browser内の「Mesh_1」を選択した状態で「Apply and Close」をクリックします。
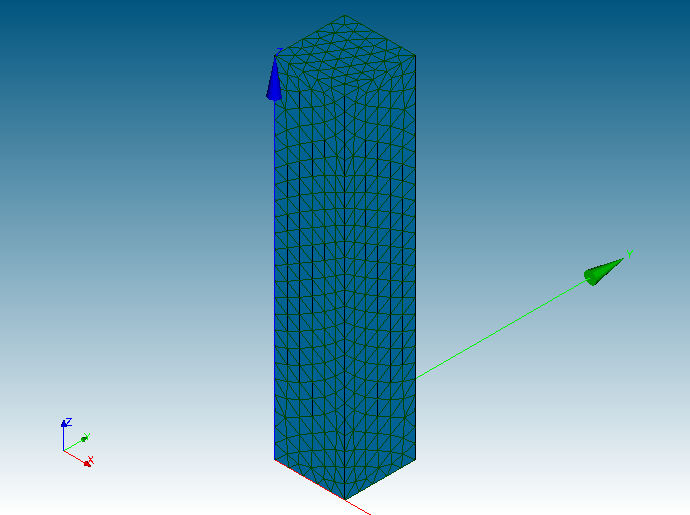
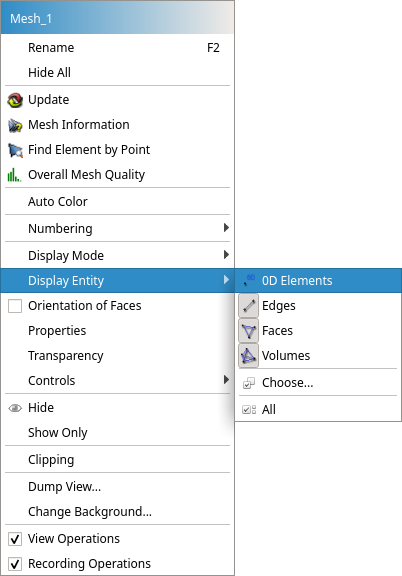
次に、Object Browser内の「Mesh_1」を選択した状態で、モデルが表示されている画面で右クリックをし、「Display Entity」>「0D Elements」を選択します。これで、さきほど作成した0Dの要素が表示されます。
グループの作成
次にグループの作成を行います。
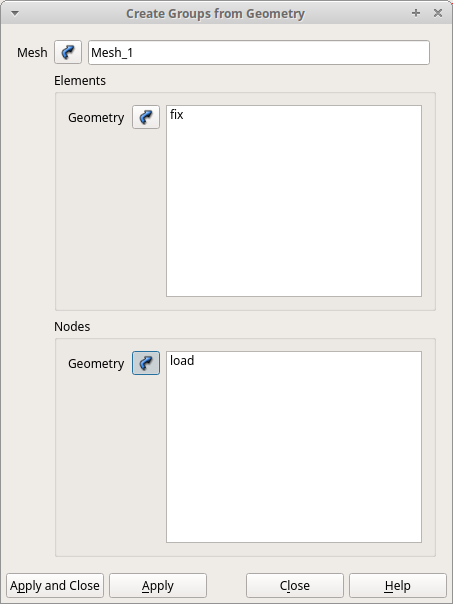
Object Browser内「Mesh_1」を選択した状態で、「Mesh」>「Create Group from Geometyr」を選択します。Object Browser内で「Geometry」>「Box_1_1」>「load」と展開し、Nodesグループに「load」グループを選択します。同様に、Elmentsグループに「fix」グループを選択します。「Apply and Close」を選択します。
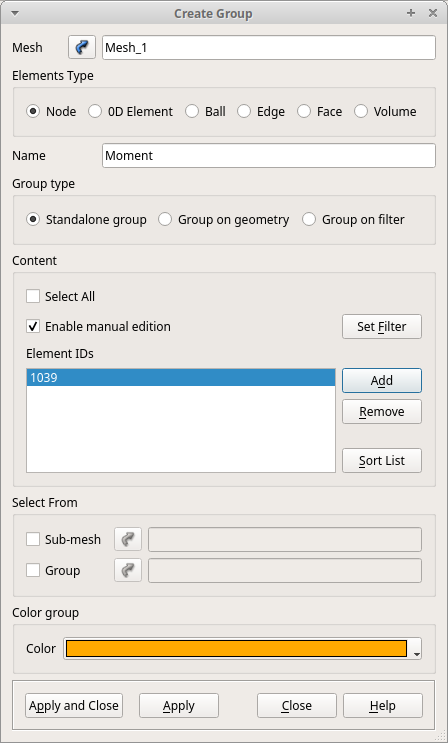
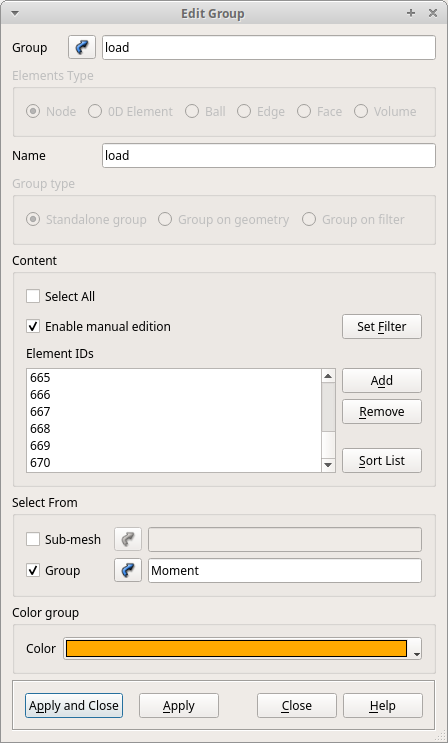
次に、モーメントを作用させる点のグループを作成します。Object Browser内「Mesh_1」を右クリックし、「Create Group」を選択します。Elements Typeを左端「Node」に変更し、「Group type」は「Standalone group」に変更します。
「Name」欄にはグループ名を入力します。 今回は"Moment"とします。
「Content」内の「Enable manyual editon」にチェックを入れ、モデルが表示されている画面から荷重点を選択し、「Add」をクリックします。今回は左欄に「1039」と表示されました。
「Apply and Close」をクリックします。
次に、さきほど作成した「load」グループに荷重点を追加します。Object Browser内より、「Mesh_1」>「Group of Nodes」を展開します。表示された「load」を右クリックし、「Edit Group as Standalone」を選択します。
表示されたウィンドウ内「Select From」より「Group」の欄にチェックを入れ、Object Browser内の「Moment」グループを選択します。「Content」欄の右にあるをクリックし、「Elements IDs」に「1039」が追加されたことを確認して「Apply and Close」をクリックします。
ここで、Meshモジュールで作成したグループの確認を行います。
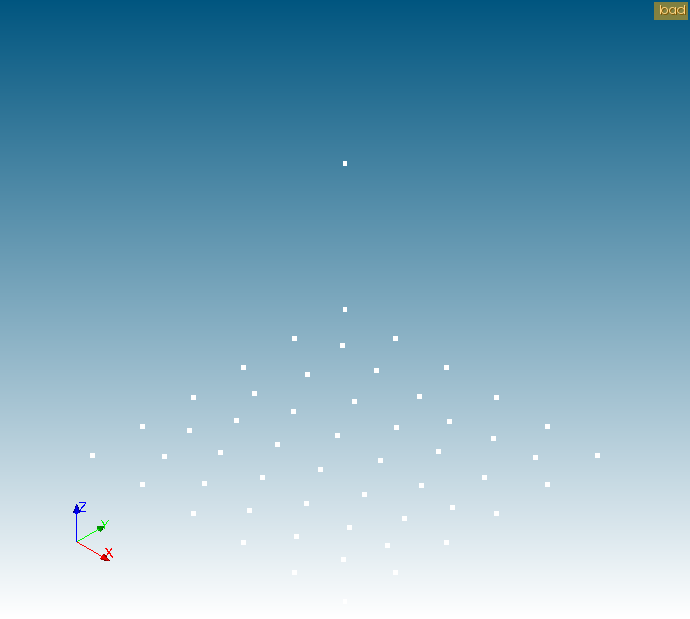
Object Browser内、「Mesh_1」>「Group of Nodes」>「load」で右クリックをし、「Show Only」を選択します。次の図のように表示されているか確認します。
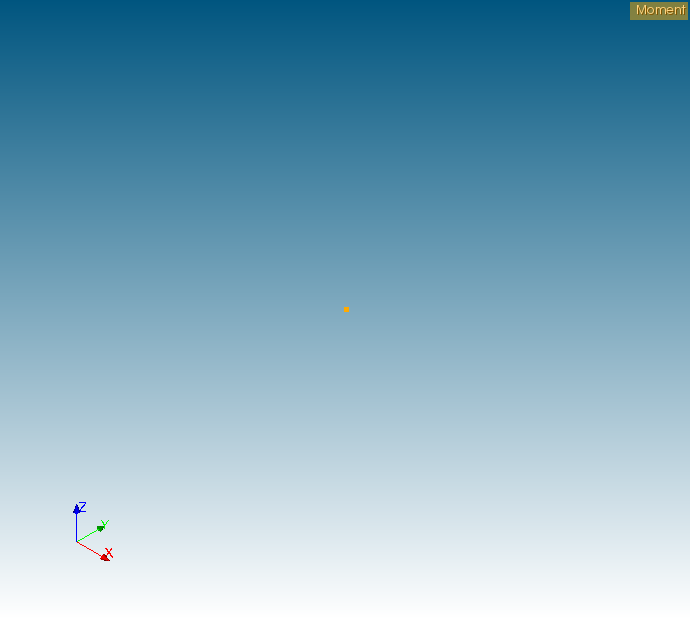
次に「Moment」グループの確認も、「load」グループと同様に行います。
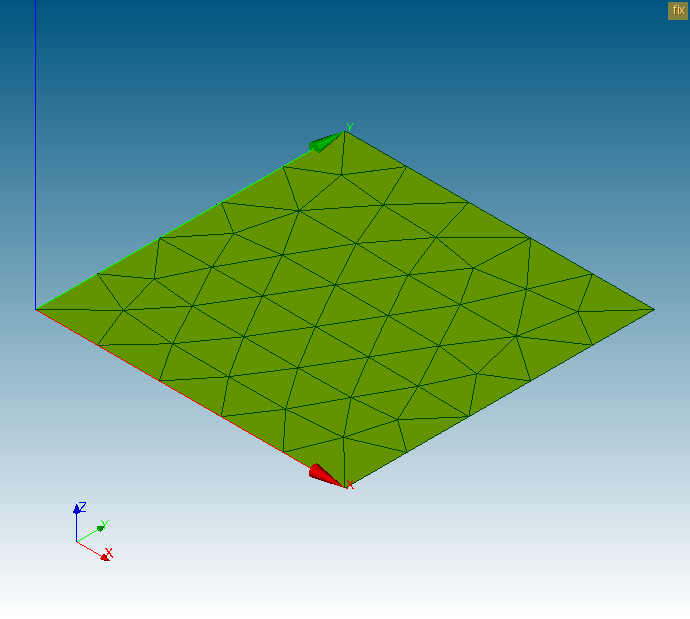
最後に「fix」グループの確認を行います。
これで、グループの作成が完了しました。
解析
初めに、次の図に示す部分を選択してAsterStudyモジュールに変更します。
解析コードの作成
初めに、アシスタント(ウィザード)を用いてIsotropic liner elastic(等方性線形弾性)解析コードの作成を行います。
- メニューより、「Operations」>「Add Stage Assistant」>「Isotropic liner elastic」を選択します。
- Introductionが表示されるので、「Next>」を選択します。
- メッシュの選択画面になり、「Specify input mesh」と聞かれるので、デフォルトの「Mesh_1」のままで「Next>」を選択します。
- モデルの選択画面になり、「What kind of model do you want to work on?」と聞かれるので、 デフォルトの「3D」のままで「Next>」を選択します。
- 材料定数の設定画面になり、ここでは解析を行うモデルの ヤング率Eとポアソン比$\nu$を入力します。
- 今回は材質を「Steel」とするので、ヤング率Eに"2.1e5"(N/mm$^2$)、ポアソン比$\nu$に"0.3"を入力
- 「Next>」を選択します。
- 拘束条件を設定します。
- 自由度を拘束するグループを追加するために、「Select mesh groups and apply degree on them」ボタンを選択して、行を追加します。
- Groupの「Edit...」を選択し、fixグループを選択し、 「OK」を選択します。
- DX、DY、DZに"0"を入力し、「Next>」を選択します。
- 荷重条件を設定します。後に編集を行うので、ここではダミーの値を入力します。
- 圧力荷重を負荷するグループを追加するために、「Select mesh groups and apply pressure on them」ボタンを選択して、行を追加します。
- Groupの「Edit...」を選択し、fixグループを選択し、「OK」を選択します。
- 「Next>」を選択します。
- 最後に結果ファイルを保存する場所を聞かれるので、「Specify output result file」欄右の「Browse...」ボタンから任意の場所に保存(今回はtorque.rmedという名前で保存)し、「Finish」を選択します。
解析コードの編集
アシスタント(ウィザード)が終了すると、Code_Asterの解析コードができるので、その編集を行っていきます。
今回はトルク解析なので、
- CREA_MAILLAGE:メッシュの設定
- AFFE_MODELE:モデルの割り当て
- AFFE_CARA_ELEM:要素の設定
- AFFE_CHAR_MECA:境界条件の設定
- MECA_STATIQUE:解析のSolver設定
- CALC_CHAMP:ポスト処理の設定
-
IMPR_RESU:結果出力の設定
の項目について編集を行います。
CREA_MAILLAGE:メッシュの設定
Code_Aster内の単一節点の作成
Code_Asterで何かに荷重や変位をかけるためには、モデルと材料が割り当てられていなければなりません。
これは、この場合、荷重や変位を与えるために使用する単一節点にも適用されます。
その節点に離散要素を作成します。
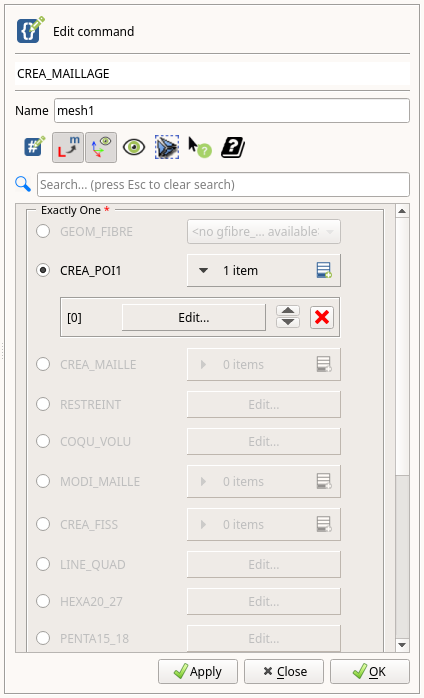
- 「DATA Settins」画面でStage_1を選択してから、 「Mesh」>「CREA_MAILAGE」をクリックします。
- 「Name」設定を"mesh1"に変更します。
- CREA_POI1をチェックし、「0 items」横のアイコンをクリックして、行を追加します。
- 「Edit...」をクリックします。
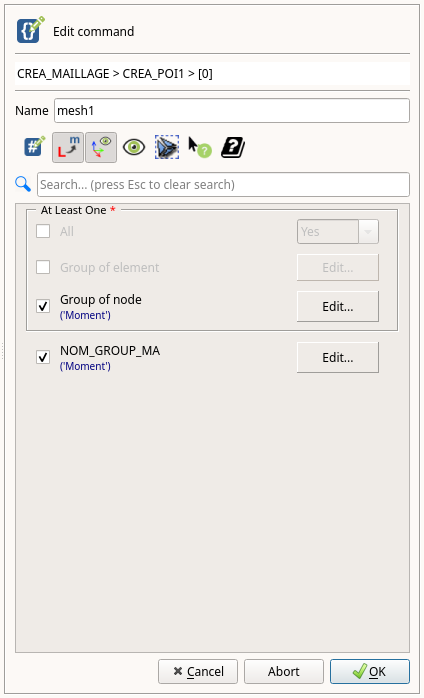
- Group of nodeをチェックし、「Edit...」をクリックします。
- 「Manual selection」に直接、"Moment"と入力し、「OK」をクリックします。
- 同様に、NOM_GROUP_MAをチェックし、「Edit...」をクリックします。
- 「Manual selection」に直接、"Moment"と入力し、「OK」をクリックします。
- **Mesh(mesh(LIRE_MAILLAGE))**をチェックします。
- 「OK」をクリックし設定を確定します。
mesh1 = CREA_MAILLAGE(CREA_POI1=_F(GROUP_NO=('Moment', ),
NOM_GROUP_MA=('Moment', )),
MAILLAGE=mesh)
-
CREA_MAILLAGE:元のメッシュから新しいメッシュを作成
-
CREA_POI1:
ノードグループ'Moment'から1つのノードを含むメッシュを作成します -
これは後でモデルとマテリアルをノードに割り当てるために必要です。 -
NOM_GROUP_MA: 新しいメッシュグループ'Moment'の名前 -
Salomeで作成したノードグループ'Moment'と同じ名前になります。
-
CREA_POI1:
(ドキュメント[U4.23.02]はCREA_MAILLAGEの使用について詳しく説明しています)
AFFE_MODELE:モデルの割り当て
ここでは、オブジェクトの構成要素にモデルを割り当てます。
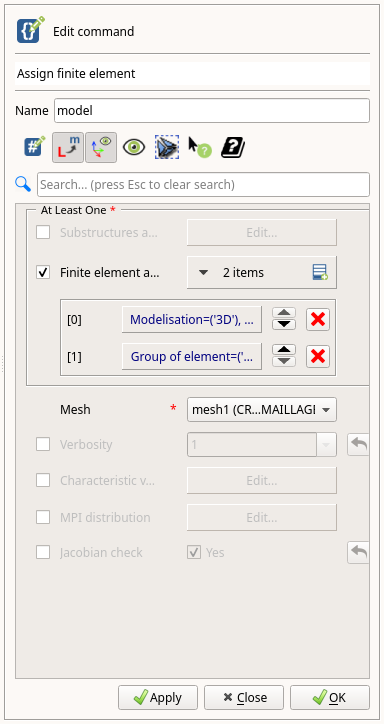
- 「DATA Settins」画面のAFFE_MODELEを右クリックし、「Edit...」を選択します。
- すでにチェックが付いているFinite element assignementの「1 items」横のアイコンをクリックして、行を追加します。
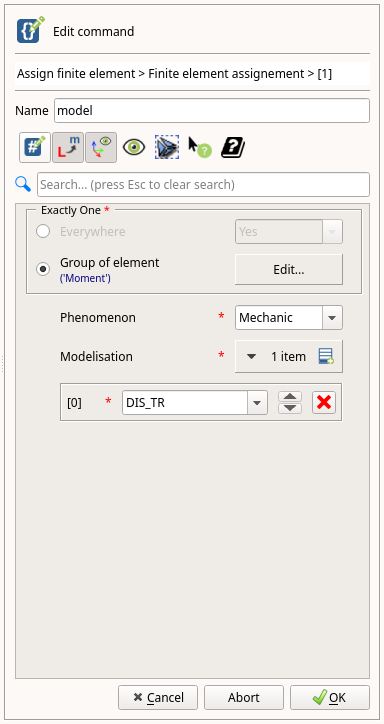
- 追加された行の「Edit...」をクリックします。
- Group of elementにチェックを入れ、「Edit...」をクリックします。
- 「Manual selection」に直接、"Moment"と入力し、「OK」をクリックします。
- PhemomenonにMechanicを選択します。
- Modelisationの「0 items」横のアイコンをクリックして、行を追加します。
- 追加された行にDIS_TRを選択します。
- Meshを**mesh1(CREA_MAILLAGE)**に変更します。
- 「OK」をクリックし、設定を確定します。
model = AFFE_MODELE(AFFE=(_F(MODELISATION=('3D', ),
PHENOMENE='MECANIQUE',
TOUT='OUI'),
_F(GROUP_MA=('Moment', ),
MODELISATION=('DIS_TR', ),
PHENOMENE='MECANIQUE')),
MAILLAGE=mesh1)
-
AFFE_MODELE: モデルの割り当て、ここでは便利な名前は 'Model' です
- MAILLAGE:'mesh' というメッシュに割り当てます
- AFFE_1:すべてのものに3Dメカニカルモデルを割り当てる
-
AFFE_2:単一節点の'負荷'に離散モデルを割り当てる
-
MODELISATION=DIS_TR:
Translation(平行移動)とRotation(回転)の機能を持つdiscrete(離散)モデルを割り当てる
-
MODELISATION=DIS_TR:
AFFE_CARA_ELEM:単一節点の設定
繰り返しになりますが、単一節点は計算の範囲内で動作するために何らかの特性を持っていなければなりませんし、それは0Dであって3Dではないので、それを記述しなければなりません。
ここでは、1次元ビーム(POUTRE)の特性を記述するときと同じように、あまり意味がありませんが、記述しなければなりません。
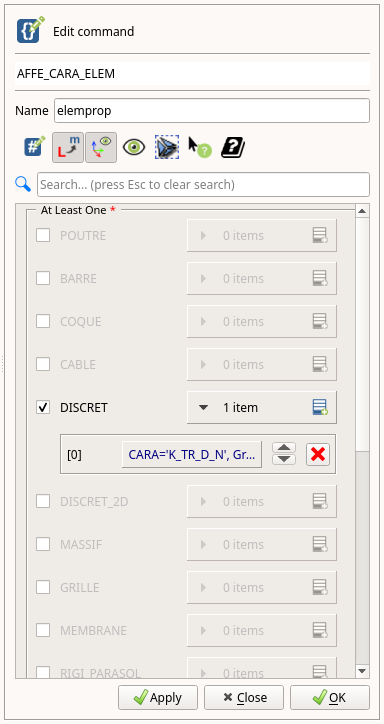
- 「Model Definition」>「AFFE_CARA_ELEM」をクリックします。
- DISCRETをチェックし、「0 items」横のアイコンをクリックして、行を追加します。
- 追加された行の「Edit...」をクリックします。
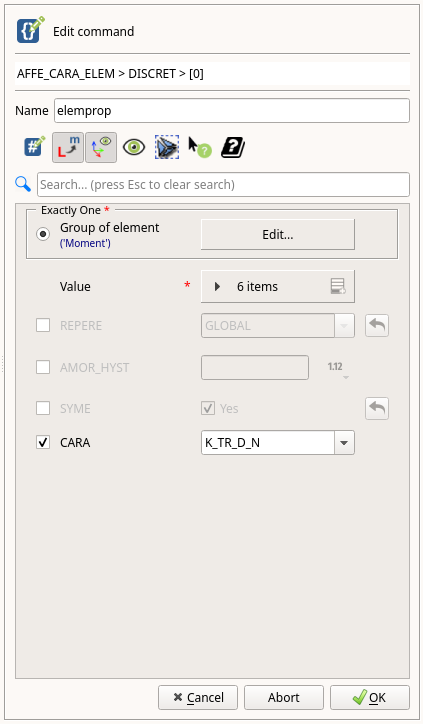
- CARAをチェックし、K_TR_D_Nを選択します。
- Group of elementをチェックし、「Edit...」をクリックします。
- 「Manual selection」に直接、"Moment"と入力し、「OK」をクリックします。
- Valueの「6 items」にそれぞれ"1"を入力します。
- 「OK」をクリックします。
- 「OK」をクリックし、設定を確定します。
elemprop = AFFE_CARA_ELEM(DISCRET=_F(CARA='K_TR_D_N',
GROUP_MA=('Moment', ),
VALE=(1.0, 1.0, 1.0, 1.0, 1.0, 1.0)),
MODELE=model)
-
AFFE_CARA_ELEM:MODELE=Modelを使用して要素の特性を割り当てる。
-
DISCRET=discrete(離散化)
-
CARA=K_TR_D_N:
- K:離散要素の種類を表す:K(剛性), M(質量)またはA(減衰)
- TR:変位と回転が可能
-
D:これは対角行列です -
もう1つの設定はこの文字を省略することです(そうすると行列全体を入力しなければなりません) - N:節点です(seg2要素はL)
-
CARA=K_TR_D_N:
-
DISCRET=discrete(離散化)
節点「荷重」が構造物の荷重を誘導するためだけに使用され、荷重の伝達に影響を与えないことを確認するために、すべてに1.0(DX、DY、DZ、DRX、DRY、DRZ)の値が割り当てられます。
AFFE_CARA_ELEMの使用と値の意味についての詳細は、[U4.42.01]セクション13.3.3を参照してください。
AFFE_CHAR_MECA:境界条件の設定
- 「DATA Settins」画面のコンセプト名'mecach'のAssign Mechanical
Loadを右クリックし、「Edit...」を選択します。 - ダミーで設定したPRES_REPのチェックを外します。
- FOECE_NODALにチェックし、「0 items」横のアイコンをクリックして、行を追加します。
- 追加された行の「Edit...」をクリックします。
- Group of nodeにチェックし、「Edit...」をクリックします。
- Momentを選択し、「OK」をクリックします。
- MZにチェックし、"1000000"を入力します。
- LIAISON_SOLIDEにチェックし、「0 items」横のアイコンをクリックして、行を追加します。
- 追加された行の「Edit...」をクリックします。
- Group of nodeにチェックし、をクリックします。
- 'load'を選択し、「OK」をクリックします。
- 「OK」をクリックします。
- 「OK」をクリックし、設定を確定します。
mecach = AFFE_CHAR_MECA(FORCE_NODALE=_F(GROUP_NO=('Moment', ),
MZ=1000000.0),
LIAISON_SOLIDE=_F(GROUP_NO=('load', )),
MODELE=model)
-
AFFE_CHAR_MECA:機械的負荷を割り当てます。以前に割り当てられたモデルを使用します
-
FORCE_NODALE:節点荷重を課す。
-
GROUP_NO=Moment
- MZ=1000000.0:単一節点「Moment」には、Z軸を中心としたモーメント荷重が割り当てられます。
-
GROUP_NO=Moment
-
LIAISON_SOLIDEです。ここでマジックが起こる
- GROUP_NO='load':節点グループ'load'は、完全にリジッドな接続**(LIAISON_SOLIDE)**を持つように指示されています
- 節点'load'が移動すると、グループ内の残りの節点も同様に移動します。
- (MODELE=Model)
-
FORCE_NODALE:節点荷重を課す。
MECA_STATIQUE:解析のSolver設定
- 「DATA Settins」画面のStatic Mechanical Analysisを右クリックし、「Edit...」を選択します。
- Structure element characteristicにチェックします。
- 「OK」をクリックし、設定を確定します。
result = MECA_STATIQUE(CARA_ELEM=elemprop,
CHAM_MATER=materfl,
EXCIT=(_F(CHARGE=mecabc),
_F(CHARGE=mecach)),
MODELE=model)
-
MECA_STATIQUE:'result'という線形計算を作成
- CARA_ELEM=elemprop:単一節点'Moment'に対して以前に定義した特性elempropを含む
- CHAM_MATER=materfl:材料'materfl'を使用して材料フィールドを計算します
-
EXCIT
- CHARGE=mecabc:'mecabc'で割り当てられた変位拘束を使用します。
- CHARGE=mecach:'mecach'で割り当てられた負荷を使用します。
- **MODELE='Model'**を使用します
CALC_CHAMP:ポスト処理の設定
ポスト処理を次のように追加します。
result = CALC_CHAMP(reuse=result,
CHAM_MATER=materfl,
CONTRAINTE=('SIGM_ELNO', 'SIGM_NOEU'),
CRITERES=('SIEQ_ELNO', 'SIEQ_NOEU'),
MODELE=model,
RESULTAT=result)
- reuse(使う結果名)=reslin(ここでは再利用)
-
CONTRAINTE:応力
- SIGM_ELNO:応力(要素)
- SIGM_NOEU:応力(節点)
-
CRITERES:基準
- SIEQ_ELNO:相当応力(要素)
- SIEQ_NOEU:等価応力(節点)
IMPR_RESU:結果出力の設定
「Post Processing」>「CALC_CHAMP」で結果出力を次のように修正します。
IMPR_RESU(FORMAT='MED',
RESU=_F(MAILLAGE=mesh,
NOM_CHAM=('DEPL', 'SIEQ_NOEU', 'SIGM_NOEU'),
RESULTAT=result),
UNITE=80)
- FORMAT=MED:出力するバイナリ形式にMED形式を指定
-
NOM_CHAM
- DEPL:変位量
- SIEQ_NOEU:等価応力(節点)
- SIGM_NOEU:応力(節点)
- RESULTAT=reslin
- UNITE(論理ユニット番号)=80
解析コード
DEBUT(LANG='EN')
mesh = LIRE_MAILLAGE(FORMAT='MED',
UNITE=20)
mesh1 = CREA_MAILLAGE(CREA_POI1=_F(GROUP_NO=('Moment', ),
NOM_GROUP_MA=('Moment', )),
MAILLAGE=mesh)
model = AFFE_MODELE(AFFE=(_F(MODELISATION=('3D', ),
PHENOMENE='MECANIQUE',
TOUT='OUI'),
_F(GROUP_MA=('Moment', ),
MODELISATION=('DIS_TR', ),
PHENOMENE='MECANIQUE')),
MAILLAGE=mesh1)
elemprop = AFFE_CARA_ELEM(DISCRET=_F(CARA='K_TR_D_N',
GROUP_MA=('Moment', ),
VALE=(1.0, 1.0, 1.0, 1.0, 1.0, 1.0)),
MODELE=model)
mater = DEFI_MATERIAU(ELAS=_F(E=210000.0,
NU=0.3))
materfl = AFFE_MATERIAU(AFFE=_F(MATER=(mater, ),
TOUT='OUI'),
MODELE=model)
mecabc = AFFE_CHAR_MECA(DDL_IMPO=_F(DX=0.0,
DY=0.0,
DZ=0.0,
GROUP_MA=('fix', )),
MODELE=model)
mecach = AFFE_CHAR_MECA(FORCE_NODALE=_F(GROUP_NO=('Moment', ),
MZ=1000000.0),
LIAISON_SOLIDE=_F(GROUP_NO=('load', )),
MODELE=model)
result = MECA_STATIQUE(CARA_ELEM=elemprop,
CHAM_MATER=materfl,
EXCIT=(_F(CHARGE=mecabc),
_F(CHARGE=mecach)),
MODELE=model)
result = CALC_CHAMP(reuse=result,
CHAM_MATER=materfl,
CONTRAINTE=('SIGM_ELNO', 'SIGM_NOEU'),
CRITERES=('SIEQ_ELNO', 'SIEQ_NOEU'),
MODELE=model,
RESULTAT=result)
IMPR_RESU(FORMAT='MED',
RESU=_F(MAILLAGE=mesh,
NOM_CHAM=('DEPL', 'SIEQ_NOEU', 'SIGM_NOEU'),
RESULTAT=result),
UNITE=80)
FIN()
理論解との比較については、「ApplyingTorque」2と「Salome-Meca2019による丸棒のねじり解析」3に詳しく述べられています。
謝辞
貴重な情報をOpenCAE Users Wiki上に公開してくださった柴田先生、GPLライセンスでCAELinux上に公開してくださったClaus Andersen氏に心から感謝します。
-
信高未咲. Salome の使い方 – トルク解析 - 第14回勉強会:H240602 - OpenCAE Users Wiki. http://opencae.gifu-nct.ac.jp/pukiwiki/index.php?%C2%E8%A3%B1%A3%B4%B2%F3%CA%D9%B6%AF%B2%F1%A1%A7H240602, June 2012. (Accessed on 12/22/2020) ↩
-
Claus Andersen. Contrib:Claws/Code Aster/10 x cases/torque - CAELinuxWiki. https://www.caelinux.org/wiki/index.php/Contrib:Claws/Code_Aster/10_x_cases/torque, April 2011. (Accessed on 12/22/2020) ↩ ↩2
-
@femlabo-toyo. Salome-Meca2019による丸棒のねじり解析 - Qiita. https://qiita.com/femlabo-toyo/items/b28ef117ef003ad652f0, May 2020. (Accessed on 12/22/2020) ↩