はじめに
初心者がざっとニューラルネットワークを理解していくという記事です。
前提として今は研究をしていない学士卒が書いた記事ということは念頭においてください🙇
ニューラルネットワーク(NN)について
深層学習(ディープラーニング)に必要。もともと機械学習の手法の一つだったが、ハード機器の発達で深層学習ができるようになることでニューラルネットワークという手法が発達した。
まずは一次関数で直感的にNNを理解しよう!
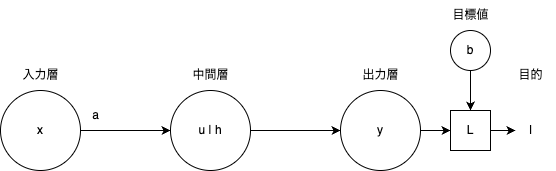
入力値xに対して、パラメータaが最適化された(*)関数yの出力は
y^* = a^*x + b
と表せます。
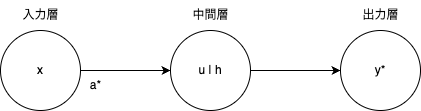
※ u|hについては後ほど解説します
どのように最適化されるかは、例えばy = ax + bにおいてyの目標値はtであるとします(y = tの時、$y = y^*$)。目標値に近づくようにパラメータaを最適化していきますというお話です。今回、t = bであるとします。
ここでの最適化とは、どの入力値xに対しても(任意のxに対して)yの値ができる限りbに近づくようパラメータaを最適化しようっていうお話しです。
では、y = ax + bの学習の進み方を見てみましょう。
学習の進み方(一次)
順伝播(一次)
最初にxが入力された時、u = ax + bが計算されます。(線形変換)
uが0以上で結果をそのまま、小さいと0に変換 (非線形変換、活性化処理)
\begin{equation}
h =m(u) = ReLU(u) =
\begin{cases}
u & (u \geqq 0) \\
0 & (u \lt 0)
\end{cases}
\end{equation}
※ 活性化関数mがReLUの場合
y = h出力層に中間層の計算結果が渡されます。
yと目標値(今回は最小値)bの差の二乗をとります。(目的化処理)
l = L(y) = (b - y)^2
yを目標値bに近づける処理をこの後するためです。この時のLを目的関数と呼びます。この後の操作ではlの最小化問題と考えてパラメータが更新されます。
※ 便宜上、目的化処理と呼んでいますが、単に、出力層に目的関数を設定するっていう認識で大丈夫です。```
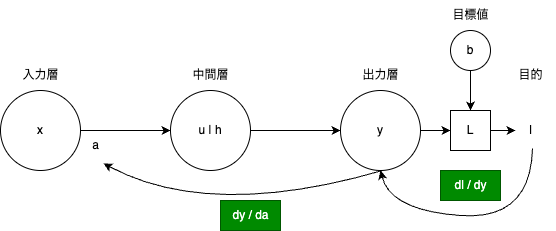
逆伝播(一次)
このb - yからaを最適化します(最適化処理)
a \leftarrow a -\eta\frac{d l}{d a} = a - \eta\frac{d l}{d y}\frac{d y}{d a} (\etaは学習率)
aの値を更新します。(a - dl/daの部分は最適化の方法でまた変わります。)
学習率を設定することで徐々に目標値に近づくことを可能とします。パラメータによっては学習が収束しないなんてことも良くあるのでこういう値は大事です。
そして再度、順伝播...
この順伝播、逆伝播を繰り返します。
※ Δとdの違いについて、Δ(デルタ)は変化や差分を表すための演算子であり、微小変化を表現するためには不適切です。機械学習の文脈では、微分(dy/dx)を使用してパラメータを更新することが一般的です。今回の場合だとdy/daの部分はΔでも対応可能かもしれませんが、dl/dyの部分ではΔだと正確に表現できません。詳しくは微分の定義
最適化後(一次)
学習が終わったら、(目標値に限りなく近づいたら)
y、aが最小値bに近づくように最適化(*)されています。この時
y^* = a^* x + b
これで任意の入力値に対して、yが最小値b付近の値を出力するようになりました!
やったね!
※ $y^*$の値についてですが、$a^*x+b$という一連の操作の結果であると認識してください。これが結構抜けてる人が多いので、抜けてたなという人は最初から読んでください。数式を言語化して理解できているかは結構重要です。この後もそれを意識してみてください。
※ 本来はbも最適化の対象とすることがありますが、今回の場合、簡単のためにaに絞っています。以下でも、b値はハイパーパラメータとして扱います。
ベクトル、行列で理解してみよう!
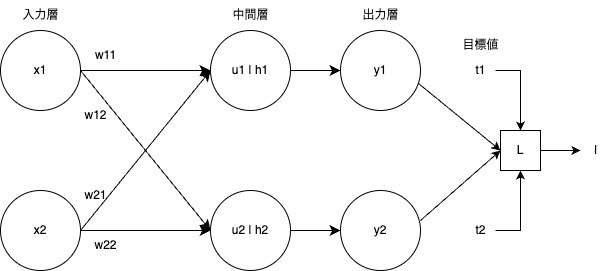
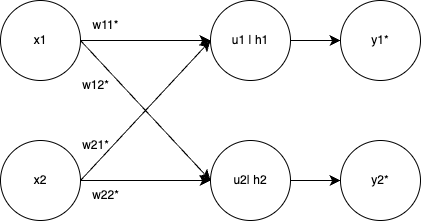
同様に、入力ベクトルxに対して最適化(*)されたパラメータ関数yの出力ベクトルは
\begin{align}
\mathbb{y}^* = \boldsymbol{W}^{*} \mathbb{x} + \mathbb{b}
\end{align}
Wは重み行列、bはバイアスベクトルです。簡単のためにこれらの値は
\begin{align}
\mathbb{y}^* = (y_1^*, y_2^*),
\boldsymbol{W}^* =
\begin{pmatrix}
w_{11}^{\,*} & w_{12}^{\,*} \\
w_{21}^{\,*} & w_{22}^{\,*}
\end{pmatrix},
\mathbb{x} = (x_1, x_2),
\mathbb{b} = (b_1, b_2)
\end{align}
目的関数もしっかり定義してみましょう。今回は単なる差ではなく平均二乗誤差(MSE)を用います。
L = \frac{1}{N} \sum_{i=1}^{N} {(t_{\,i} - y_{\,i})^2}
Nはベクトルの要素数で、tは目標値です。今回はN = 2で定義します。
一応言語化してみましょう。目標ベクトル$(t_1, t_2)$に出力ベクトルを近づけたい。みたいな感じですかね。
学習の進み方(vec)
順伝播(vec)
線形変換
\begin{align}
u_1 &= \omega_{\,11}\,x_1 + \omega_{\,21}\,x_2 + b_1 \\
u_2 &= \omega_{\,12}\,x_1 + \omega_{\,22}\,x_2 + b_2
\end{align}
非線形変換
今回も活性化関数はReLUでいきましょう
\begin{align}
h_1 &= ReLU(u_1) \\
h_2 &= ReLU(u_2)
\end{align}
※ 活性化関数は、ベクトルを受け取ったとしても基本的には要素ごとに適用されます
y_1 = h_1, y_2 = h_2
目的化処理
\begin{align}
l = L(y) &= \frac{1}{2} \sum_{i=1}^{2} {(t_{\,i} - y_{\,i})^2} \\
&= \frac{1}{2}\{(t_1 - y_1)^2 + (t_2 - y_2)^2\}
\end{align}
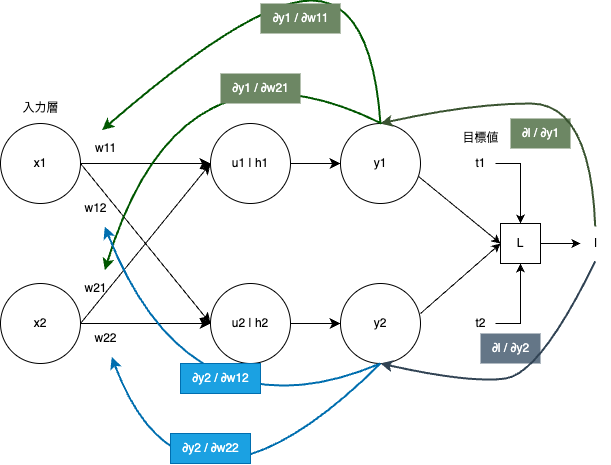
逆伝播(vec)
パラメータが一気に増えます。ベクトルになると更新したいパラメータが複数あるので、微分ではなく勾配で逆伝播します。
w_{11} \leftarrow w_{11} - \eta\frac{∂l}{∂w_{11}} = w_{11} - \eta\frac{∂l}{∂y_1}\frac{∂y_1}{∂w_{11}}
他同様なので省略します。
※このように書けるのは、lを関数で表したときは合成関数になるのですが、この関数一つ一つが微分可能であるからです。一部ReLUなどは微分不可能な点(x=0)がありますが、これは劣微分などで解消します。
最適化後(vec)
入力ベクトルxに対して目標値に近づくように最適化(*)されたパラメータ関数yの出力ベクトルは
\begin{align}
\mathbb{y}^* = \boldsymbol{W}^{*} \mathbb{x} + \mathbb{b}
\end{align}
普段私たちが使ってるAIはこの最適化がされ続けて一旦学習を終えたもの、というのが大まかな認識です。※大まかです。
最適化されたパラメータによって構成された「関数」は普段私たちが何気なく使用してる関数と見かけ上何も変わりません。※見かけ上。
ここで疑問、「NNじゃなくても普通の関数(アルゴリズム)でいけるのでは?」
全くもってその通りです。NNは手法の一つで場合によっては既存のアルゴリズム使ったほうがいい場合もあります。(例えばルービックキューブとか、AI使うまでもなく状態管理のアルゴリズムでいけますね。)
何が便利なのって人間では思いつかないようなアルゴリズムを学習によって導いてくれる点。
NNについて本題
構造のお話
入力層、中間層、出力層はもちろんスカラー、ベクトル、行列だけじゃないです。テンソルで表現されます。
0次元テンソルがスカラー、
1次元テンソルがベクトル※、
2次元テンソルが行列...(以下略)
みたいなのです。
※3次元ベクトルは1次元テンソルのベクトルの要素数が3というイメージです。ここ間違いやすいです。
この辺りは学習対象に依存してきます。画像や音声、それぞれで次元が変わるので、、
学習対象にあった入力層、出力層を設計したり、学習対象のデータを加工して入出力に合うようにしたり(データの前処理)して、中間層は通常、特徴量を抽出し、入力データをより表現力の高い特徴量空間にマッピングするために使用されます。中間層は複数の層にまたがることがほとんどです。
この辺りは有名どころの論文とか、その解説記事を読んで感覚(本質)を掴んでくしかないです。頑張ってください。ざっと基礎を数ヶ月でさらいたい人には個人的にはゼロから作るdeep learningシリーズがおすすめ。基礎がないのに最新技術追っても余程の人じゃない限りわからないと思うので基礎はおろそかにしたらダメだと思います。
層と層の関係のお話
層と層の結合については、全結合や畳み込み、再帰が挙げられます。
全結合: k層目のn個のノードとk+1層目のj個のノード同士が全て(n×j個)繋がってるイメージ。上の例ではこれを採用
畳み込み: k層目の距離が近いノードを関連づけ、k+1層のノードに渡す。k層目の特徴量がk+1層目に表れているイメージ。画像向け
再帰: k層目のノードの出力結果を何度かk層目に入れるイメージです。時刻を保持するのに向いてる。
目的関数
目的関数には損失関数や誤差関数などがある。筆者は損失関数しか知りません。
学習の最終的な目標値に近づけるために必要な関数というイメージ。
学習における何を最小化したいのとか、どういうふうに学習を進めればいいのっていう指標です。
損失関数には、MSE(平均二乗誤差)とかがあります。
詳しくは、調べてみてください。
基本的な計算(順伝播)
線形変換と非線形変換をこの順で繰り返し計算していきます。
一つの層には複数のニューロンがあります。
その層が複数あり、ちょうど下の記事の最初にある図みたいなイメージです。
線形変換
直感で理解しようの項目に載せてるのでなんとなく分かってると思ってますが、
入力ベクトル$h$と重み行列W、バイアスベクトル$b$を使って
\boldsymbol{W}\mathbb{h} + \mathbb{b}
と変換すること。詳しくはこちら
厳密にはアフィン変換ですが、ディープラーニングの文脈では+bを含む操作も線形変換と呼ばれることが多いです。
非線形変換
Sigmoid関数とか、ReLUとかありますね。
非線形変換の説明に詳しく載ってますが、活性化処理というのをすることで、このニューロンで計算された線形変換がどれくらい妥当な値かというのを数値化していると筆者は認識しています。
計算(逆伝播)
ここは勾配で重みを更新するやつですね。微分ではなく厳密には勾配ですので勾配と呼びましょう。目的関数の最適化、重みの更新にもいろいろと方法があります。最適化手法、最適化アルゴリズムと呼ばれることが多いです。有名な記事を載せときます。
そもそもなんで学習に逆伝播が必要か?
一つに、メモリ問題で学習時にニューラルネットワークの一つ一つのニューロン全ての計算結果を保持できないことがほどんどです。更新したいパラメータのみを記憶しておき、それを最終的な計算結果から勾配で導く逆伝播はメモリ問題を解決してくれます。
また、解析的に解けない問題を解いてくれるというのも強みです。
完全に理解した
とは言ってません。筆者も完全に理解はしてないです。
参考にしたものなど
終わりに
(ただの感想というか所感なので読み飛ばして大丈夫です。お疲れ様でした!!!!)
数式なしでもわかる!という記事も散見されますが、違うと思います。
言葉を概念に当てて、概念をなんとなく理解した気になってる。もちろん概念という領域に、言葉という一つ一つの言語領域によって近づけていくことで理解することもある。しかし、それには多くの試行錯誤が必要でそれこそ、私たちが機械学習的に大量のデータ、事例を帰納的にを学習する必要がある。せっかく数式という明確な定義があるのだからそれを使って理解した方が早いと思います。また、数式なしで言葉のみで正確に定義しようとするとかなりの文字数になります。友達が強化学習系の卒業論文を数式なしで書いてましたが、本来30ページ相当のものを50ページ強に拡張しており、「読むのに時間がかかった」「嫌がらせだよね笑」と教授が苦悶していたのを覚えています。数式は言葉で表すことができますが、数式それ自体が言語なのでわざわざテキストに変換せずに一発で脳内にぶち込む方が絶対に気持ちいいです。食わず嫌いせずに数学の基礎から学びましょう。ちなみに筆者も基礎から学び直し中です。
最後まで読んでいただき、ありがとうございました。