ボックスカウント法によるフラクタル次元解析を3次元でやってみた

はじめに

構造物の 美しさ を定量的に評価しよう.
という研究を行っています．
その定量化手法としてフラクタル次元というものを一つの指標としています．

そして，フラクタル次元を求めるためにはボックスカウント法という方法を用いるのですが，
これを3次元で扱っている例が調べても出てこなかったので，記事にしてみました．

フラクタル次元とは

フラクタル次元
Wikipediaにはこのようにあります．
簡単に捉えると1次元と2次元，2次元と3次元の間の次元を，非整数の値で表現できるものです．
複雑さを表すことができるんですね．
これを用いて景観や絵画といったものの定量的評価が行われています．

フラクタル次元解析

今回は例として，200×200×200の立方体を
1で初期化した3次元のnumpy配列として実験してみます．

実際はSTLファイルを読み込み
numpy-stlを用いて配列化を行います．
(詳細は今後執筆予定です)

ボックスカウント法

ボックスカウント法に関してはここの記事が分かりやすいと思いますので，リンクを張らせていただきます．
表面粗さ曲線のフラクタル解析

これを3次元的に考えます．

1. 立方体を格子状に分割
2. 格子内に物体が含まれていればカウント
3. 格子の辺の長さをgrid_size，カウント数をnとする
4. log(grid_size)とlog(n)をプロット
5. 最小二乗法による線形回帰を行う
6. その回帰係数をフラクタル次元とする

この格子のサイズを順々に変えていきます．

ボックスに含まれる要素をカウントする関数

3次元配列をx方向→y方向→z方向の順で走査し
1の判定はnp.anyで行います．

3d_fractal.py

def count(arr, x, y, z, b):
    i = j = k = 0
    b_tmp  = b
    b_tmp2 = b
    ct = 0

    j_tmp = b
    k_tmp = b
    while k < z:
        while j < y:
            while i < x:
                if (np.any(arr[i:b, j:j_tmp, k:k_tmp] == 1)):
                    ct += 1
                i += b_tmp
                b += b_tmp
            # 折り返し
            j += b_tmp2
            j_tmp += b_tmp2
            b = b_tmp2
            i = 0
        # 折り返し
        k += b_tmp2
        k_tmp += b_tmp2
        b = b_tmp2
        j = b_tmp2

        i = 0
        j = 0

main関数

格子サイズを200から1/2ずつ100, 50, ... と1になるまでcount()の処理を繰り返します．
格子サイズが1のときのカウントは200×200×200 = 80,00,000になるはずです．

3d_fractal.py

def main():

    x = y = z = 200

    graph_x = []
    graph_y = []

    array3d = np.ones((x, y, z))
    ct_1 = np.count_nonzero(array3d == 1)

    grid_size = max(x, y, z)

    while grid_size >= 1:
        n = count(array3d, x, y, z, grid_size)
        graph_x.append(math.log(grid_size))
        graph_y.append(math.log(n))
        print(grid_size, n)
        print (math.log(grid_size), math.log(n))
        grid_size = int(grid_size / 2)

線形回帰

カウントした結果から線形回帰を行います．
回帰の処理にはscikit-learnのクラス
sklearn.linear_model.LinearRegressionを使用します．

3d_fractal.py

    graph_x = np.array(graph_x).reshape((len(graph_x), 1)) # 1列にする
    graph_y = np.array(graph_y).reshape((len(graph_y), 1))

    model_lr = LinearRegression()

    # 予測モデル作成
    model_lr.fit(graph_x, graph_y)

    plt.xlabel("log(grid_size)")
    plt.ylabel("log(n)")

    plt.plot(graph_x, graph_y, 'o')
    plt.plot(graph_x, model_lr.predict(graph_x), linestyle="solid")

    plt.grid()
    plt.show()

    # フラクタル次元 = 回帰係数
    fractal = model_lr.coef_[0][0] * -1 

    print("Fractal : ", fractal)

結果

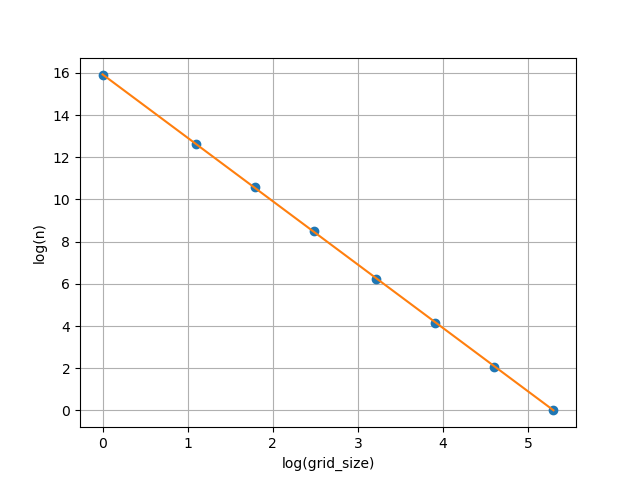
こちらが結果の対数グラフです．
横軸に格子サイズのlog
縦軸にカウント数のlog
これの回帰係数がフラクタル次元ということになります．

200 1
5.298317366548036 0.0
100 8
4.605170185988092 2.0794415416798357
50 64
3.912023005428146 4.1588830833596715
25 512
3.2188758248682006 6.238324625039508
12 4913
2.4849066497880004 8.499640032168648
6 39304
1.791759469228055 10.579081573848484
3 300763
1.0986122886681098 12.614077858172898
1 8000000
0.0 15.89495209964411
Fractal :  3.004579190748091

結果はこのようになりました．
フラクタル次元は3.004579190748091
ということで，ほぼ理論値ですね．
200から繰り返しをした際に，25/2 = 12と割り切れない場合が生じたため少しずれが出てしまいました．

まとめ

• ボックスカウント法で3次元的フラクタル次元解析の検証ができました．
• STLファイルからダイレクトにフラクタル次元を算出する方法を次回書きたいと思います．

参考文献

"表面粗さ曲線のフラクタル解析", 児野武朗, (2010) , 長野県工技センター研報, No.5, p.P52-P55.