この記事はDeNA 21新卒×22新卒内定者 Advent Calendar 2021の18日の記事です。
こんにちは、22新卒の@John_barderaです。研究に苦しんでいます。
DeNA 21新卒×22新卒内定者アドカレなんて面白そうなものがあったので飛びついてみたものの、研究かバイトしかしていません。
バイトの方は喋っちゃいけないがあったり、ちょっとマイナーめな技術を使ってたりなので必然的に研究の話をすることになりました。
時間があれば、低温調理器作ってみた!とかPC電源解体して実験用の電源作ってみた!とか電動スタンディングデスク作ってみた!とかやりたかった。。
さて今回は研究でやっていることの一部なのですが、正二十面体を使った魚眼画像の物体検出の話をします。
ただ、物体検出をやるまで書こうと思っていたのですが、研究の合間にやってる&記事のカロリーが大きかったので泣く泣く分割させていただきました。
本記事は、物体検出するために用いる正二十面体メッシュについてお話しするだけになってます。
そのうち、正二十面体の展開手法や物体検出についても書く予定です。
はじめに
みなさん、魚眼画像って知ってます?
監視カメラとかに採用とかされている魚眼レンズで撮影される画像で、真ん中が膨らみ、端がギュッとされてしまってるような画像のことです。
魚眼レンズが複数個ついた上下左右に$360^\circ$撮影可能な全天球カメラなんてものも最近はありますね。
このように歪みが大きいので、単純な方法では物体検出はできません。
なので今回は、どうにかしてこいつに対して物体検出をぶちかましてやりてぇって話です。
射影方式
中心射影
まず、魚眼画像ってどういうものなんだという話です。
一般的な画像と魚眼画像の違いはそれを撮影するレンズの射影方式にあります。
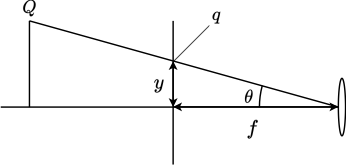
一般的な画像は、中心射影という射影方式が用いられています。
焦点距離を$f$、画角を$\theta$とするレンズでは、下の式で表されます。
y = f\cdot \tan \theta
被写体を$Q$、投影される像を$q$とすると下記のような関係になります。
これをみるとわかりますが、めっちゃ広角にしようとしても$\theta$が$90^\circ$に近づくにつれ、スクリーンからはみ出してくる場合が出てきます。
そのため、スクリーンに収まる最大の角度が製品固有の画角の限界となります。
一般的な製品としては、$\theta=57^\circ$程度らしいです。
等距離射影
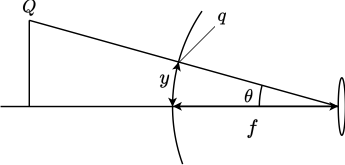
対して、魚眼画像は大抵、等距離射影が用いられます。
y = f\cdot\theta
スクリーン自体を球状に設置することで、画角が$90^\circ$だろうとスクリーンによっては撮影できるようになってます。
ただし、球状にしたスクリーンを2次元平面にすると歪んでしまうといった欠点を持ちます。
正二十面体メッシュ
正二十面隊について
等距離射影によって生成される魚眼画像が、2次元でなぜ歪んでしまうかわかっていただけたかと思います。
これを人間にもわかりやすく歪み補正するにはどうすればいいでしょうか?
代表的なのは、球を筒に見立てて平面展開する正距円筒変換だと思います。
わかりやすく処理も容易ですが、北極付近(上部)と南極付近(下部)が引き伸ばされてしまい、その点付近で精度が出ない欠点があります。
では、球を正二十面体に見立ててみてはどうでしょうか。
正二十面体は、下記のような12個の頂点と、20個の面からなる面数最大の正多面体です。
つまりは、全ての面が同じ正多角形なのでとても扱いやすい上に、存在する中で一番球に近いので、魚眼画像を投影するのにとても向いています。
というわけで今回は、サンプリング点として正二十面体(メッシュ)の各頂点を用います。
正二十面体メッシュについて
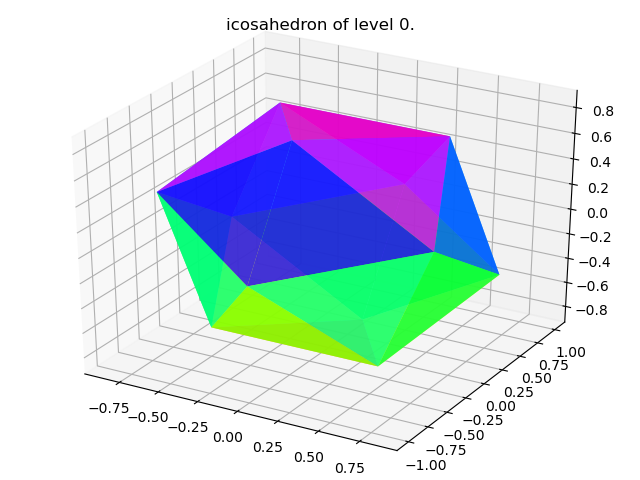
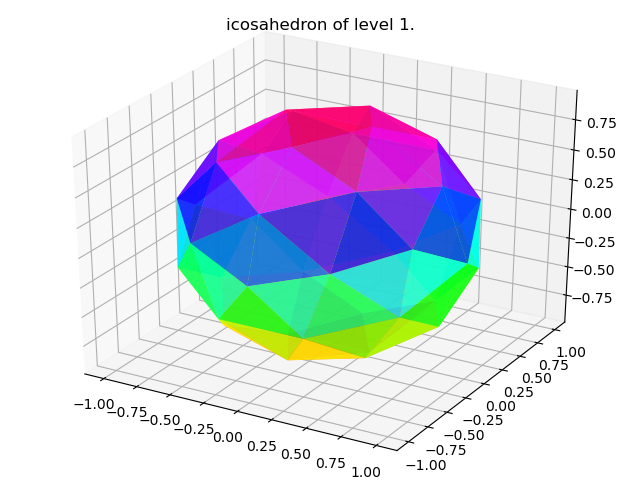
ただ、たかだか12点では、サンプリングする点としては少なすぎます。そこで、正二十面体メッシュの出番です。
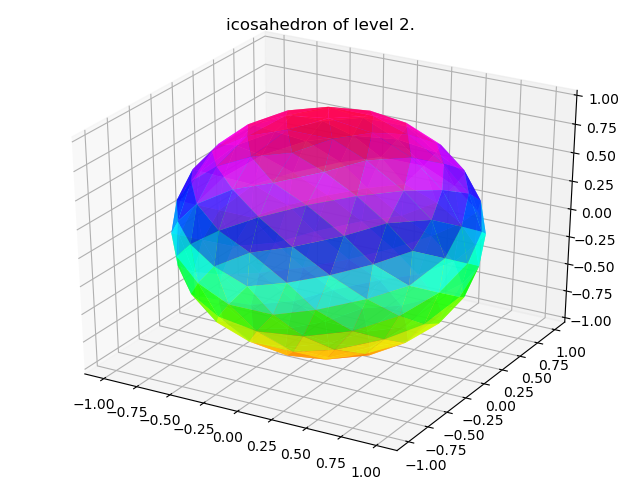
正二十面体メッシュとは、levelに応じて正二十面体の各面を4分割し、頂点を増やしたものです。
正二十面体メッシュ自体は正多面体ではありませんが、面の中にめっちゃ頂点のある正二十面体として扱うことができます。
levelごとの頂点と面の数はこんな感じ。
| level | 頂点数 | 面数 |
|---|---|---|
| 0 | 12 | 20 |
| 1 | 42 | 80 |
| 2 | 162 | 320 |
| 3 | 642 | 1280 |
| 4 | 2562 | 5120 |
| 5 | 10242 | 20480 |
コード
以下は正二十面体メッシュの座標を求めるコードになります。python3で記述しています。
ふわっと解説していきます。
import igl
import numpy as np
def get_icosahedron(level=0):
if level == 0:
v, f = get_base_icosahedron()
return v, f
# require subdivision
v, f = get_icosahedron(level - 1)
v, f = subdivision(v, f, 1)
return v, f
def subdivision(v, f, level=1):
for _ in range(level):
# subdivision
v, f = igl.upsample(v, f)
# normalize
v /= np.linalg.norm(v, axis=1)[:, np.newaxis]
return v, f
def get_base_icosahedron():
t = (1.0 + 5.0 ** .5) / 2.0
vertices = [-1, t, 0, 1, t, 0, 0, 1, t, -t, 0, 1, -t, 0, -1, 0, 1, -t, t, 0, -1, t, 0,
1, 0, -1, t, -1, -t, 0, 0, -1, -t, 1, -t, 0]
faces = [0, 2, 1, 0, 3, 2, 0, 4, 3, 0, 5, 4, 0, 1, 5,
1, 7, 6, 1, 2, 7, 2, 8, 7, 2, 3, 8, 3, 9, 8, 3, 4, 9, 4, 10, 9, 4, 5, 10, 5, 6, 10, 5, 1, 6,
6, 7, 11, 7, 8, 11, 8, 9, 11, 9, 10, 11, 10, 6, 11]
# make every vertex have radius 1.0
vertices = np.reshape(vertices, (-1, 3)) / (np.sin(2 * np.pi / 5) * 2)
faces = np.reshape(faces, (-1, 3))
# Rotate vertices so that v[0] = (0, -1, 0), v[1] is on yz-plane
ry = -vertices[0]
rx = np.cross(ry, vertices[1])
rx /= np.linalg.norm(rx)
rz = np.cross(rx, ry)
R = np.stack([rx, ry, rz])
vertices = vertices.dot(R.T)
return vertices, faces
def get_icosahedron(level=0):
if level == 0:
v, f = get_base_icosahedron()
return v, f
# require subdivision
v, f = get_icosahedron(level - 1)
v, f = subdivision(v, f, 1)
return v, f
levelに応じた正二十面体メッシュの各頂点座標と各面がどのindexの座標により構成されるかを返します。
levelが0であれば、ただの正二十面体を返しますが、そうでなければsubdivision関数で分割していきます。
def subdivision(v, f, level=1):
for _ in range(level):
# subdivision
v, f = igl.upsample(v, f)
# normalize
v /= np.linalg.norm(v, axis=1)[:, np.newaxis]
return v, f
各頂点座標と各面がどのindexの座標により構成されるかの情報から分割して、levelが1つ上の正二十面体メッシュを作っていきます。
ここでiglというpackageを使います。
幾何学処理の研究開発のためのオープンソースライブラリらしいです。
自分はこれでしか使ったことがないのですが、、
今回はupsampleだけ使っていますが、他の関数でも面白いことがいろいろできそう。
iglのご助力により面をパキッと分割したら各頂点を正規化しておきます。
def get_base_icosahedron():
t = (1.0 + 5.0 ** .5) / 2.0
vertices = [-1, t, 0, 1, t, 0, 0, 1, t, -t, 0, 1, -t, 0, -1, 0, 1, -t, t, 0, -1, t, 0,
1, 0, -1, t, -1, -t, 0, 0, -1, -t, 1, -t, 0]
faces = [0, 2, 1, 0, 3, 2, 0, 4, 3, 0, 5, 4, 0, 1, 5,
1, 7, 6, 1, 2, 7, 2, 8, 7, 2, 3, 8, 3, 9, 8, 3, 4, 9, 4, 10, 9, 4, 5, 10, 5, 6, 10, 5, 1, 6,
6, 7, 11, 7, 8, 11, 8, 9, 11, 9, 10, 11, 10, 6, 11]
# make every vertex have radius 1.0
vertices = np.reshape(vertices, (-1, 3)) / (np.sin(2 * np.pi / 5) * 2)
faces = np.reshape(faces, (-1, 3))
# Rotate vertices so that v[0] = (0, -1, 0), v[1] is on yz-plane
ry = -vertices[0]
rx = np.cross(ry, vertices[1])
rx /= np.linalg.norm(rx)
rz = np.cross(rx, ry)
R = np.stack([rx, ry, rz])
vertices = vertices.dot(R.T)
return vertices, faces
最後に正二十面体自体を返すget_base_icosahedron関数です。
まぁみていただければわかりますが、これに関しては力技です。
終わりに
いかがでしたでしょうか?
魚眼画像の面白さと、正二十面体の可能性を感じていただけたなら幸いです。
今後は、今回生成した正二十面体メッシュの半球部分のみを、等距離射影で2次元上に対応関係を得、よしなに触っていきます。
重ね重ね、この中途半端な記事にしてしまって申し訳のNASA。
qiitaで記事書くのが初めてなこともあり、読みにくい部分も多々あるかと思います。
また、間違っている部分等もあるかもしれません。
そういった場合、コメント、及び@John_barderaへのリプなどで教えていただければと思います。
ひとまず、研究を終わらせてから、この記事の続きと、電気系の工作の記事を書いてみたいと思います。
ありがとうございました。