はじめに
格子ボルツマン法の入門記事って大抵ボルツマン方程式から入るので、その辺に詳しくない人にとっては結構辛いんですよね。私もなかなか苦労しました。**衝突項ってなんだよ...なんか矢印たくさんある図なにこれ...って。
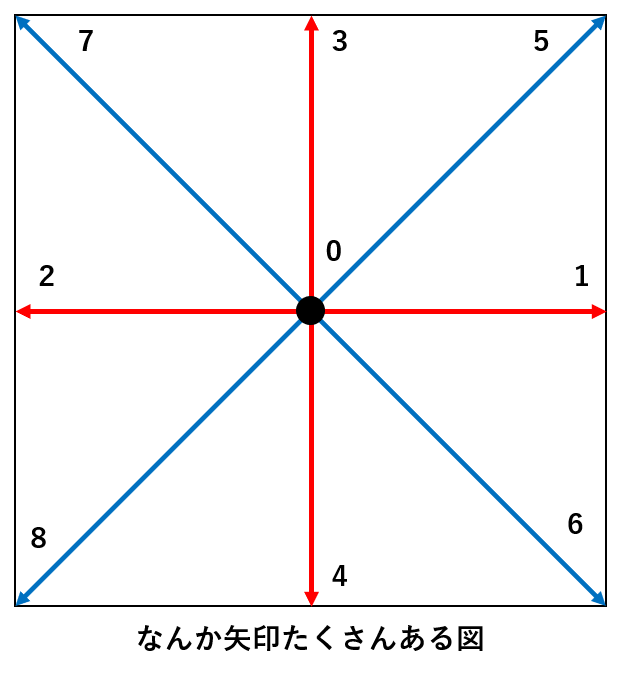
そんな「ボルツマン方程式とかあんまよく知らないけど、とりあえずざっくり格子ボルツマン法を理解したい!」**って人向けに解説記事を書いてみました。
※本記事はあくまでざっくりとした解説記事なので、厳密にはちょっと違くない?って箇所もあるかもしれません。あくまで学習のとっかかりを掴むことだけを目的にしてください。
粒子がうようよしている
格子ボルツマン法では、気体や液体の流れを多数の粒子を用いて近似します。何言ってんだ?と思うかもしれませんが、これは実際の現象にも近いですよね。例えば空気中には多数の窒素や酸素分子がうようよしています。格子ボルツマン法は、**このうようよした分子の動きを計算すれば流れもわかるだろう!**って発想から生まれた手法です。
計算上、分子を本気で記述するのはさすがに無理なので、**ちっさな粒子がたくさんうようよした結果流れが生じている!**という仮定をします。例えば、粒子が全体的に右に動いていたら、流速も右向きになるってことです。
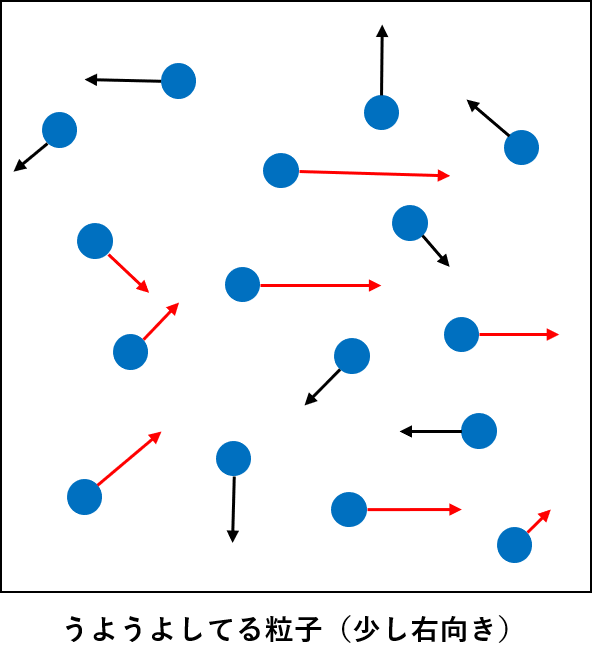
粒子の動きを計算したい!
ここまでで、**うようよした粒子の動きが把握できれば流れ方もわかりそう!**だとわかりました。でも、粒子は空間にとんでもない数(分子ならアボガドロ数のオーダーで)存在してます。しかもその粒子たちはそれぞれ別々の方向に別々の速度で動いていて...。真面目に計算するのは絶対無理です。じゃあどうするか。
ここで2つの大胆な仮定をします。「粒子の速度をみんな同じにする!」「粒子の移動方向は有限個!」。そんなことして流れなんてわかるわけないだろ!と思うかもしれませんが、これでも流れは記述できるんです。
例えば、ある1次元の領域において一定速度cで動く粒子たちがいるとします。この粒子たちの40%は右向き(v=c)、20%は左向き(v=-c)、残りの40%は静止(v=0)しているとします。この時、この領域の流速はちょっと右向きになりますよね?
他の例として、粒子たちの30%は右向きに、30%は左向きに、残りの40%は静止しているとします。この時、この領域の流速は0になります。粒子だけ見たら左右にビュンビュン飛んでるように見えますが、ちょっと離れて見れば流体としては止まって見えるはずです。
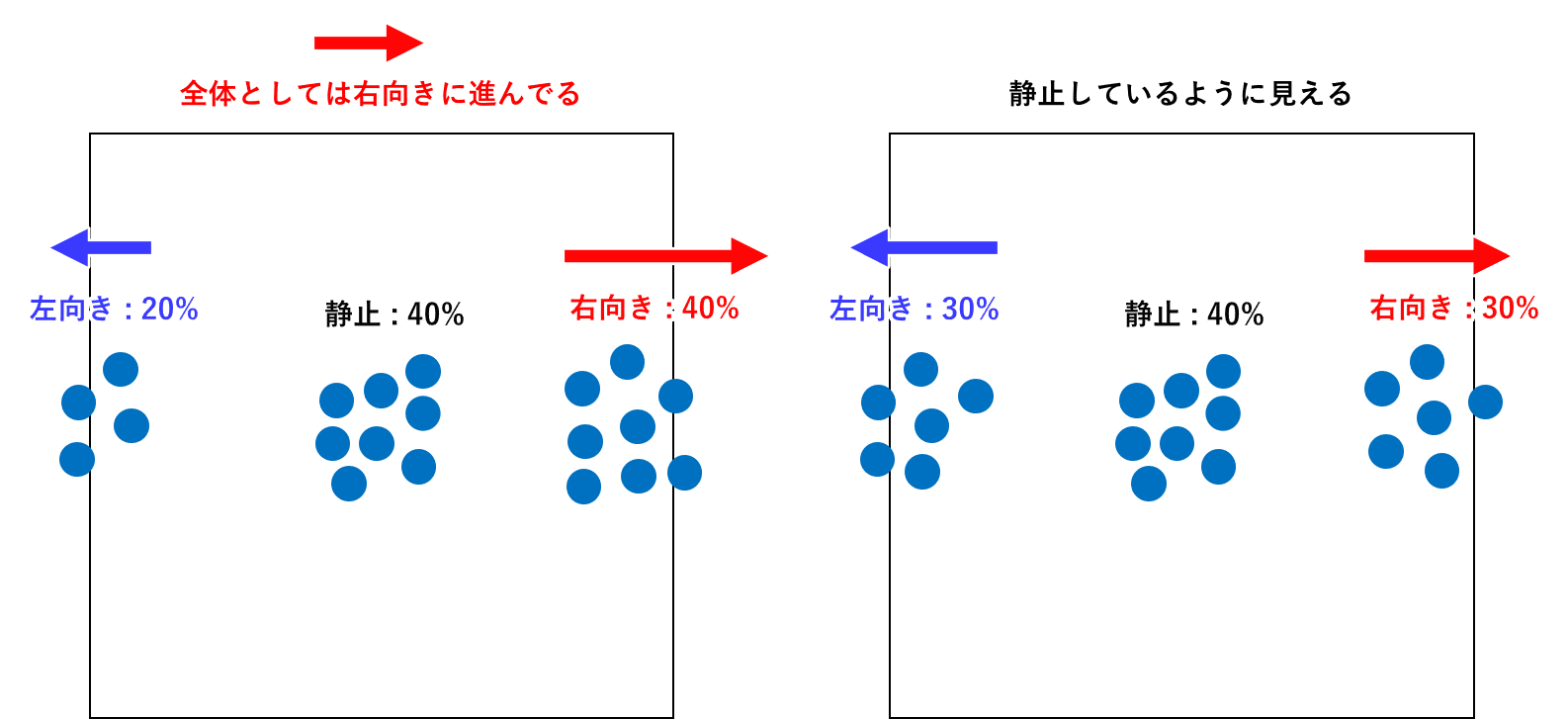
要するに、うようよしている粒子たちの進む方向の割合が分かれば何とかなりそうだとわかります。右向き粒子がめちゃめちゃ多いときは右に速い流速になりますし、ちょっと多いときは遅めの流速になります。
※身の回りの空気でも同じことが起こっていますよね。一見止まっているように見えても、気体を構成する粒子はそこら中を飛び回ってます(多分高校で勉強するはず)。完全に止まっちゃったらそれは絶対零度です。
各方向にどれだけの粒子が動いているか
ここから少し難しくなります。
どっちにどれだけ粒子が動いているかを表すために、空間を離散化した各格子ごとに分布関数fを導入します。分布関数は粒子の移動方向分だけ用意すれば良いので、1次元の場合、分布関数の方向は右、左、静止の3パターンになります。
分布関数は各移動方向における粒子の存在割合みたいなパラメータです。例えば、ある領域において右向きに移動している粒子が40%、左向きが20%、静止が40%なら、分布関数は右向きが0.4、左向きは0.2、静止は0.4になります。
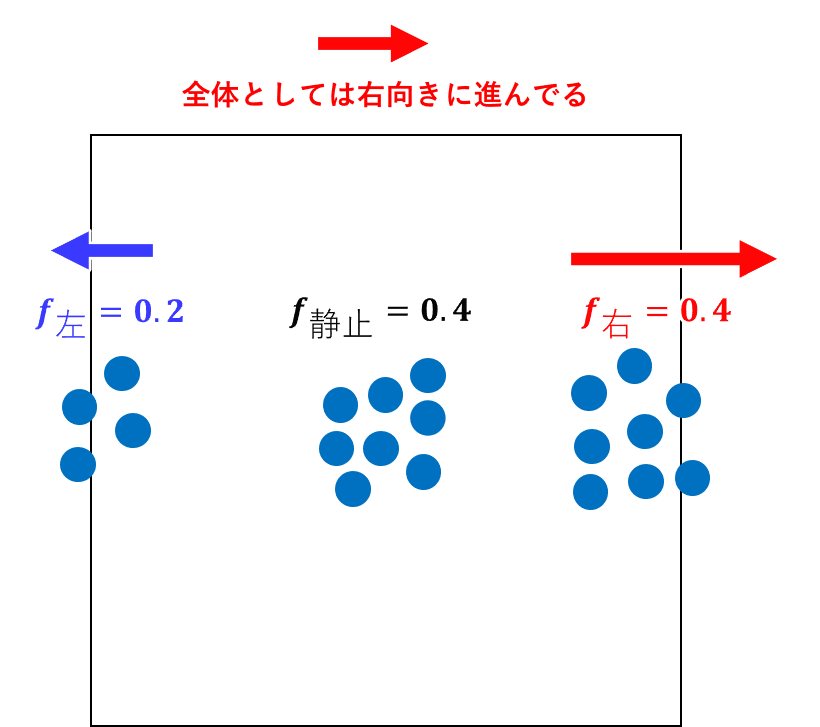
また、分布関数はその特性上、全方向の和がほぼ1(100%)になります。和が1を上回っている時、流体はその格子上で圧縮(高密度化)されていて、逆に1未満の時は流体が膨脹(低密度化)しています。
分布関数を用いることで各格子の流速がわかります。
$$
f_右-f_左 > 0 ⇔ 右向き流速\
f_右-f_左 < 0 ⇔ 左向き流速\
f_右-f_左 = 0 ⇔ 静止
$$
より具体的には、以下の式で流速が表されます。
$$
v = (f_右-f_左)c
$$
ここでは、右向きを+の方向、左向きを-の方向にしています。(計算上あり得ないですが、)例えば全ての粒子が右向きに移動しているなら、その流速は右向きにcになります。これは直感的にも正しいですね。
今回は1次元なので分布関数は右左静止の3方向でしたが、2次元・3次元に拡張するとその方向も増えます。例えば、2次元では8方向、3次元では27方向の分布関数が使われたりします。
冒頭で述べた**「なんか矢印がたくさんある図」**の正体がわかりましたね。あの矢印はこの分布関数の方向(粒子の移動方向)を表していました。
分布関数はどうやって更新するのか
格子ボルツマン法は非定常な流体解析手法なので、流速場も時間とともに変化します。流速場の時間変化はすなわち分布関数の時間変化なので、分布関数を時間とともにどんどん更新していく必要があるとわかりますね。
時間変化と来れば、タイムステップを設定する必要があります。格子ボルツマン法では、**「粒子が隣の格子へ移動する時間」**を1タイムステップとします。
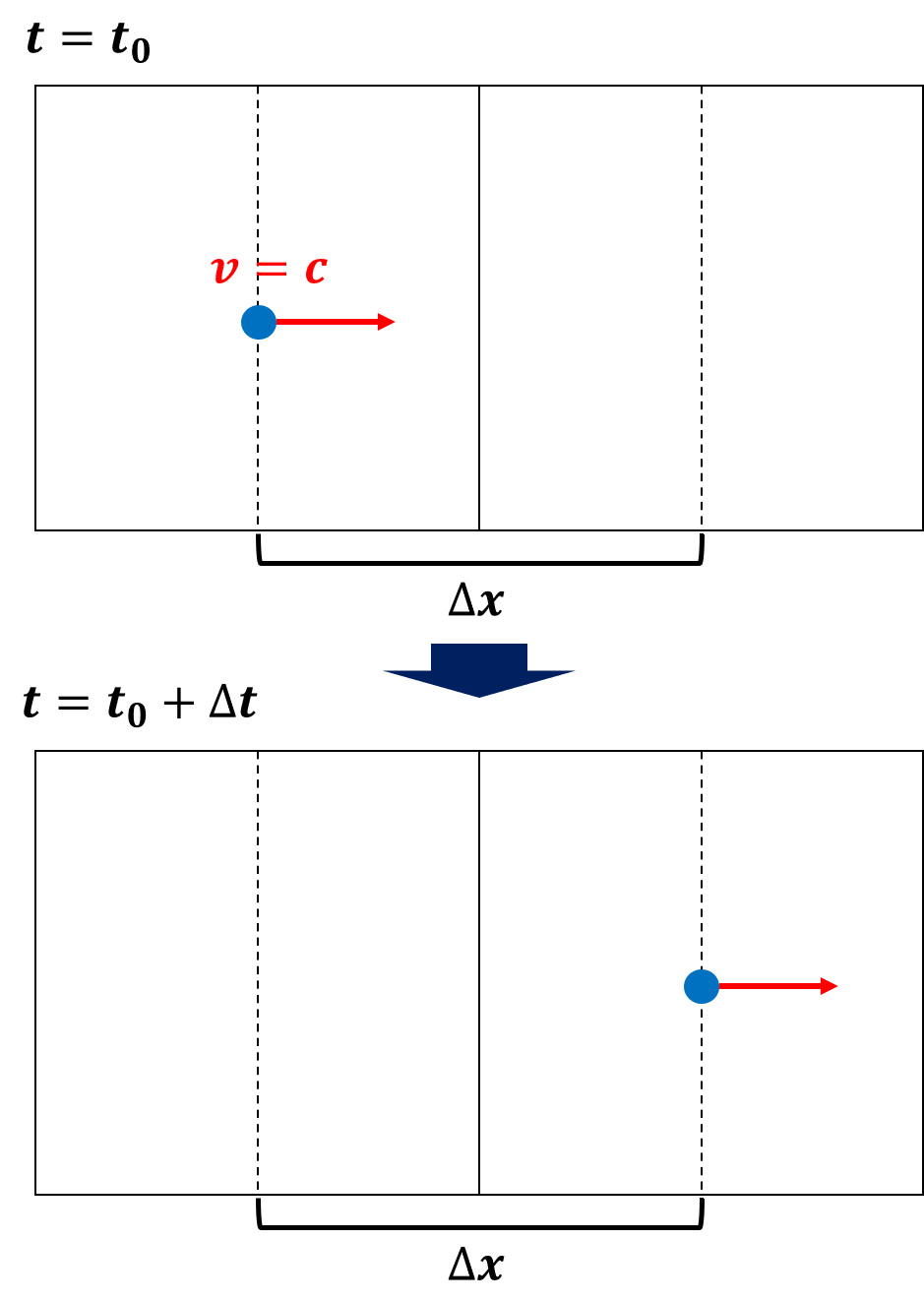
こうすることで、「格子から格子へ移動中の粒子」は考慮する必要がなくなります。つまり、タイムステップΔtは
$$
Δt=\frac{Δx}{c}
$$
になります。
並進
Δt秒が経過すると、分布関数fはそのままの値で進行方向の格子に移動します。これを、格子ボルツマン法では並進と呼びます。
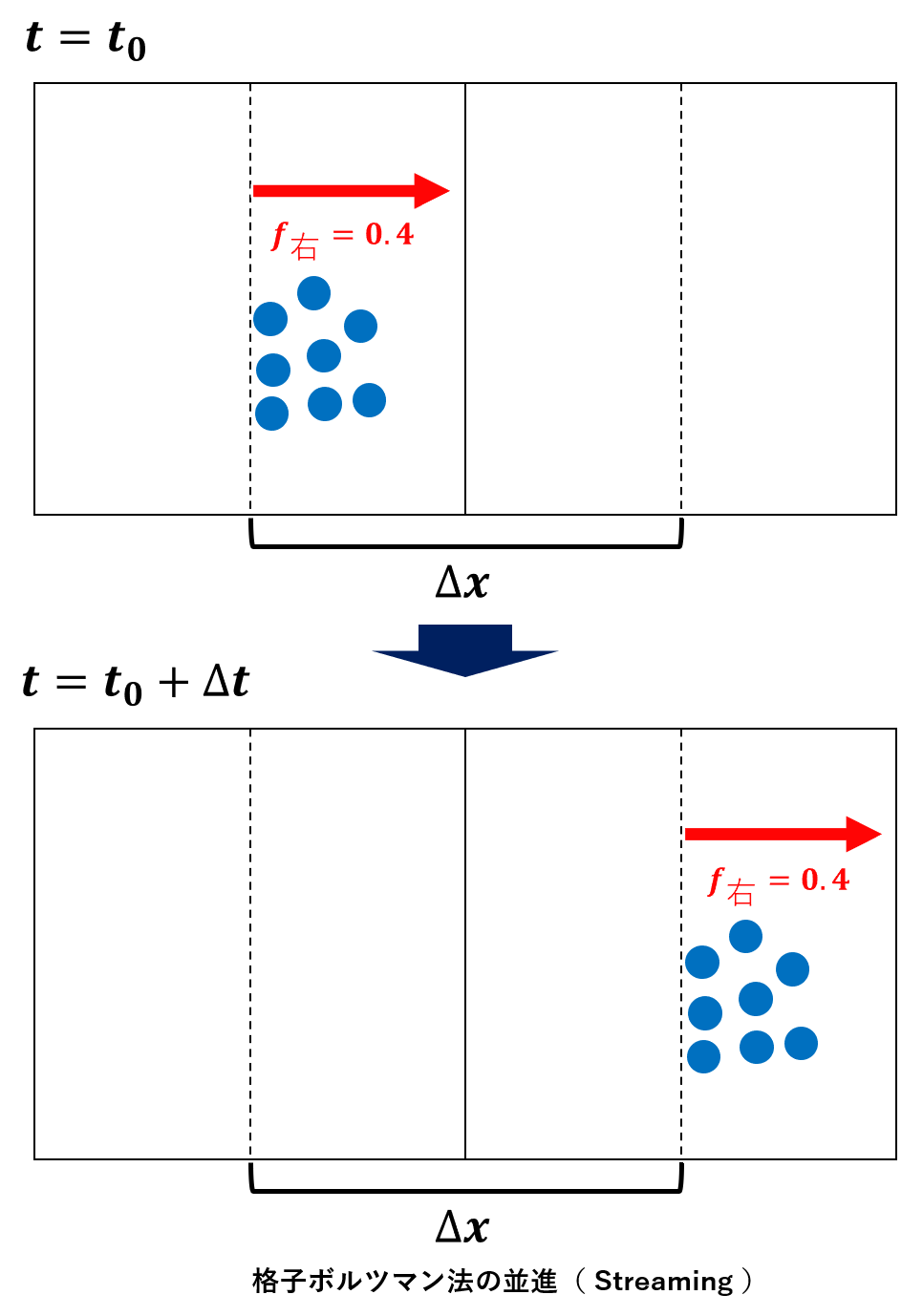
もちろん、静止した粒子は元の格子に留まります。このように各格子の分布関数が隣の格子に移動して、どんどん状況が変わっていくわけです。
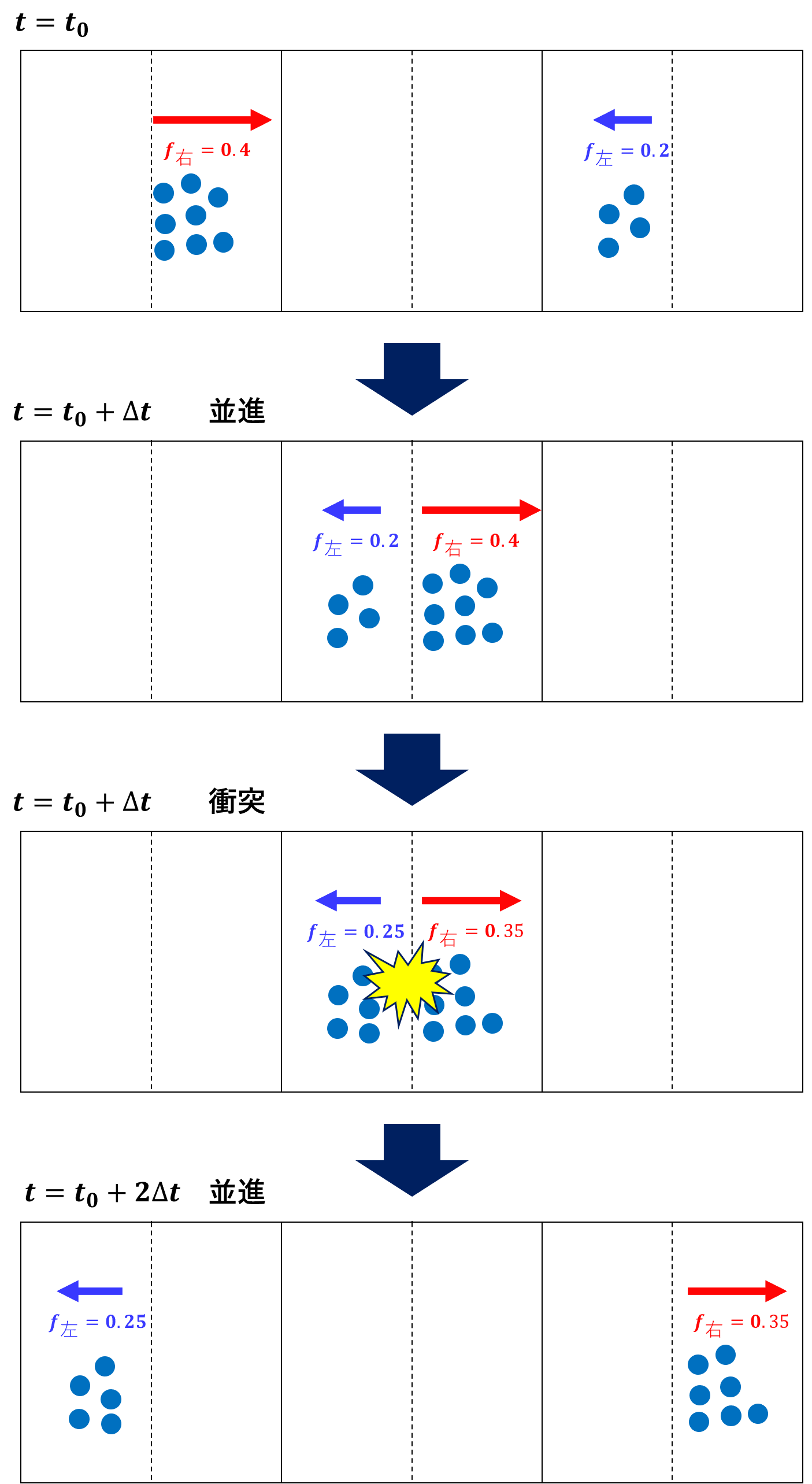
衝突
並進させれば流体の動きがわかるし、格子ボルツマン法の勉強はこれで終わりじゃん!と思うかもしれませんが、そうもいきません。並進では分布関数の値が横に移動するだけで、その大きさ自体はずっと変わりません。要するに、一度動き出した粒子たちは一生動き続けるし、反対側から別の粒子が飛んでこようがすり抜けて移動し続けます。これは現実にそぐわない感じがしますね。もう一工夫する必要があります。
並進後の粒子は各格子の中でぶつかり、運動方向が少し変わります。これを、格子ボルツマン法では衝突と呼びます。衝突で行われる計算には様々なモデルがありますが、ここでそれを紹介するのは大変なので、**「粒子たちが格子の中で衝突してその方向がちょっと変わる」**程度に覚えておいてください。
並進と衝突で流体を記述する
隣の格子に並進した粒子は、移動後の格子で反対側から来た粒子と元々そこにいた粒子と衝突します。衝突によって少し分布が変わった粒子はまた次の格子に並進して衝突し....と繰り返していきます。格子ボルツマン法では、このように並進→衝突→並進→衝突→.....の連続によって、流体の運動を表すことが出来ます。
まとめ
なるべく図をたくさん使ってわかりやすく格子ボルツマン法を解説してみました。もちろんこの記事だけでは知識として不十分なので、他の解説記事、本等の補助としてお使いください。格子ボルツマン法の勉強をする上で、少しでもお役に立てば幸いです。