【C++】3Dモデルを点群化する【内外判定アルゴリズム】

やりたいこと

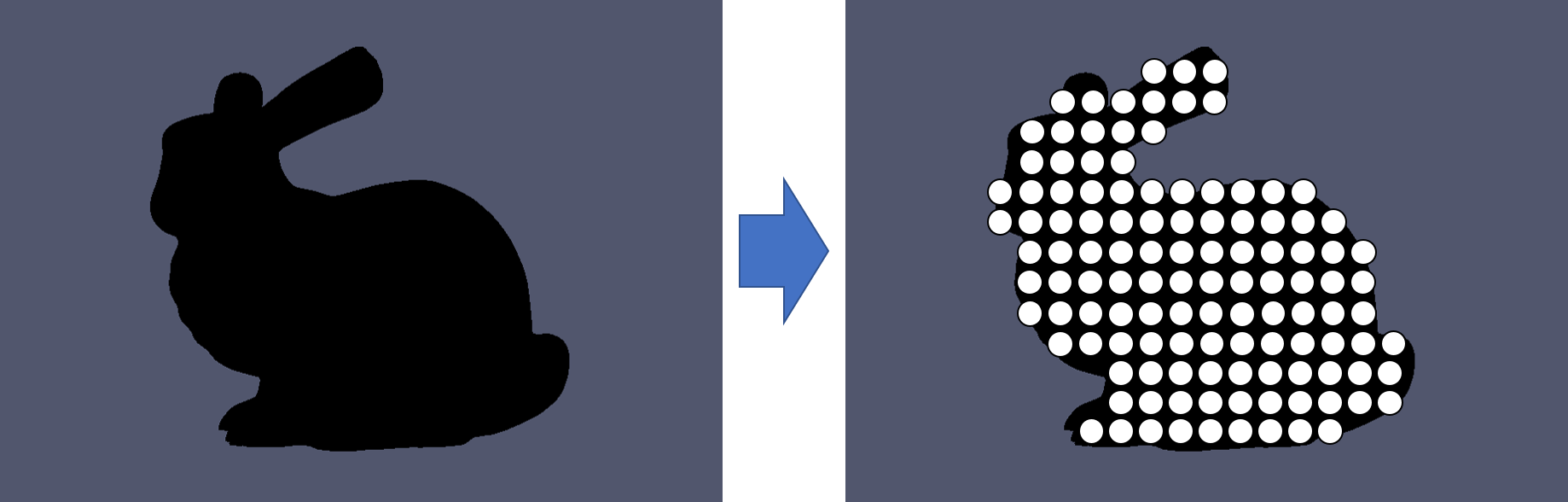
　stlファイルを読み込んで点群データに変換します。具体的には、3Dモデルを含む空間を格子状に分割して、各格子点に対して内外判定を行います。内側と判定された格子点を出力していくことで、点群データを生成します。

内外判定アルゴリズム

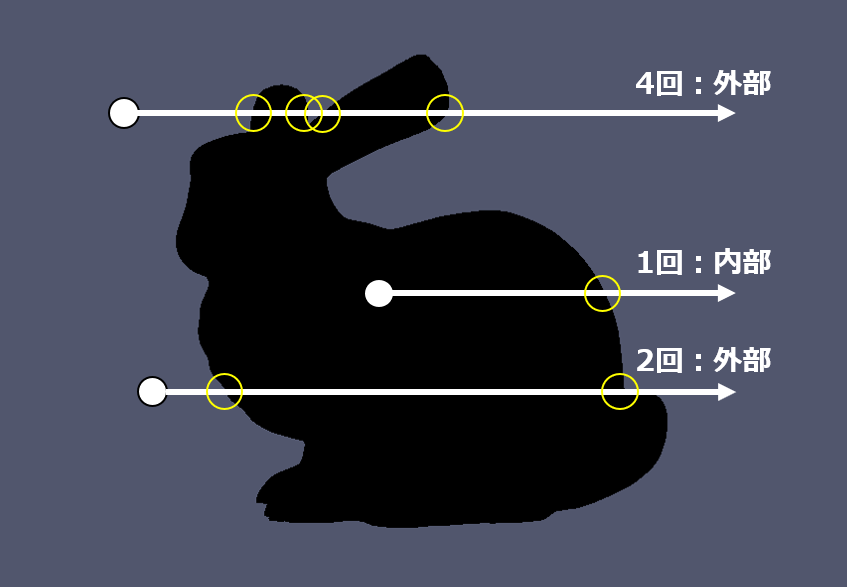
　ある点Pの内外判定アルゴリズムとして代表的なものに、「Crossing Number Algorithm」があります。このアルゴリズムは点Pから任意の方向にレイと呼ばれる半直線を伸ばし、3Dモデルの表面と交差した回数を元に内外判定を行います。交差回数が奇数回の場合は内部、偶数回の場合は外部と判定されます。計算を簡単にするために、レイは空間のx軸、y軸、z軸のいずれかに平行な方向を取ります。

レイとポリゴンの交差判定

　Crossing Number Algorithmでは、点Pから飛ばしたレイと3Dモデルを構成する各ポリゴンとの交差判定が必要になります。ここでは、実装が比較的容易かつ高速な「Tomas Mollerの交差判定アルゴリズム」を使います。こちらの記事を参考にさせていただきました。

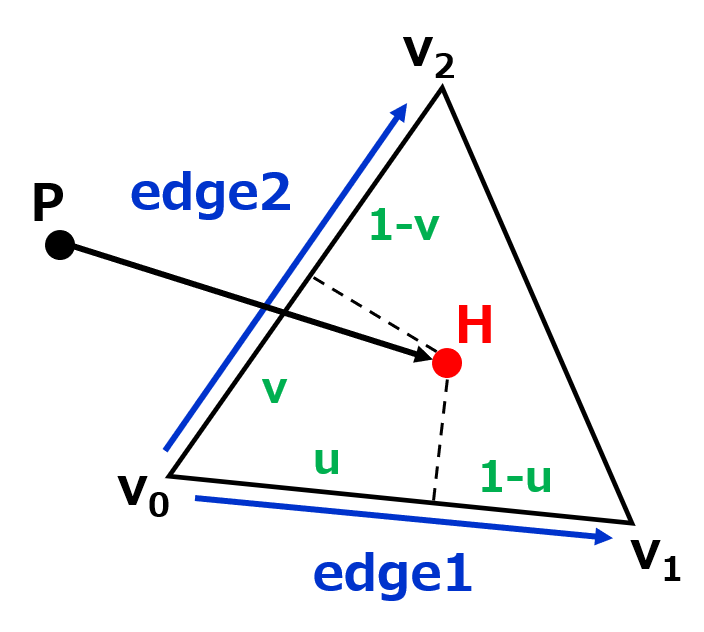
　点Pからある方向に半直線（レイ）を伸ばし、この半直線が三角形v0v1v2と交差するか否かを計算します。三角形を含む平面π上の任意の点は、

$$
\boldsymbol{H}=\boldsymbol{v_0}+\boldsymbol{edge1}*u+\boldsymbol{edge2}*v\tag{1}
$$

で表されます。ここで、v1-v0ベクトルをedge1、v2-v0ベクトルをedge2とします。一方、点Pから飛ばしたレイの軌跡は、レイの方向ベクトルをrayと置くと、

$$
\boldsymbol{H}=\boldsymbol{P}+\boldsymbol{ray}*t\tag{2}
$$

となります。今回は半直線なので、変数tはt>0を満たします。よって、これら2式よりレイと平面πの交点は

$$
\boldsymbol{v_0}+\boldsymbol{edge1}*u+\boldsymbol{edge2}*v=\boldsymbol{P}+\boldsymbol{ray}*t\tag{3}
$$

で表される方程式をu、v、tについて解けば求められます。（1）式より、uとvが

$$
0\leqq u \leqq1,\quad
0\leqq v \leqq1,\tag{4}\quad
0\leqq u+v \leqq1,
$$
を満たすとき、三角形v0v1v2上にレイと平面πの交点Hが存在します。

次に、（3）式をプログラム上で解く方法を考えます。（3）式を変形すると、
$$
\boldsymbol{edge1}*u+\boldsymbol{edge2}*v-\boldsymbol{ray}*t=\boldsymbol{P}-\boldsymbol{v_0}\tag{5}
$$
となります。この式に、連立方程式を機械的に解くことが出来るクラメルの公式を用います。クラメルの公式によって、
$$
\boldsymbol{a}*x+\boldsymbol{b}*y+\boldsymbol{c}*z=\boldsymbol{d}\tag{6}
$$
で表される連立方程式の解は
$$
x=\frac{det(\boldsymbol{d},\boldsymbol{b},\boldsymbol{c})}{det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})},\quad　y=\frac{det(\boldsymbol{a},\boldsymbol{d},\boldsymbol{c})}{det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})},\quad　z=\frac{det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{d})}{det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})}\tag{7}
$$
で与えられます。これを（4）式に適用すると、u、v、tはそれぞれ
$$
u=\frac{det(\boldsymbol{P}-\boldsymbol{v_0},\boldsymbol{edge2},\boldsymbol{-ray})}{det(\boldsymbol{edge1},\boldsymbol{edge2},\boldsymbol{-ray})} ,\quad　
v=\frac{det(\boldsymbol{edge1},\boldsymbol{P}-\boldsymbol{v_0},\boldsymbol{-ray})}{det(\boldsymbol{edge1},\boldsymbol{edge2},\boldsymbol{-ray})} ,\quad　t=\frac{det(\boldsymbol{edge1},\boldsymbol{edge2},\boldsymbol{P}-\boldsymbol{v_0})}{det(\boldsymbol{edge1},\boldsymbol{edge2},\boldsymbol{-ray})}\tag{8}
$$
と解けます。

実装

　レイとポリゴンの交差判定を各格子点について適用し、3Dモデルの点群化を行います。今回、3Dモデルはstlファイルから読み込みます。stlファイルの読み込みは過去の記事を参考にしていただけると幸いです。

　ある点Pの内外判定は下記のisCross関数で実装できます。

// 座標、ベクトル構造体
struct coord{
    float x,y,z;
    ...
};

// 行列式計算
inline float det(coord a, coord b, coord c){
    return ((a.x * b.y * c.z) + (a.y * b.z * c.x) + (a.z * b.x * c.y)
            - (a.x * b.z * c.y) - (a.y * b.x * c.z) - (a.z * b.y * c.x));
}

// ポリゴン構造体
struct polygon{
    coord v[3];
    coord normal;
    box bounding_box;
    bool isCross(coord p, coord ray);
    ...
};

// coord p		検査点座標（レイの始点）
// coord ray	レイの方向ベクトル
// coord v[]	三角形の頂点座標
bool polygon::isCross(coord p, coord ray){
    coord inv_ray = ray*(-1);
    coord edge1 = v[1]-v[0];
    coord edge2 = v[2]-v[0];
    float denominator = det(edge1,edge2,inv_ray);
    if(denominator==0) return false;
    coord d = p-v[0];
    float u = det(d,edge2,inv_ray)/denominator;
    if(u<0||1<u) return false;
    float v = det(edge1,d,inv_ray)/denominator;
    if(v<0||1<u+v) return false;
    float t = det(edge1,edge2,d)/denominator;
    if(t<0) return false;
    return true;
}

このisCross関数を各ポリゴンに対して行い、ポリゴンとの総交差数を記録します。ここで、レイはx軸に平行な方向としました。交差数が偶数ならオブジェクト外部、奇数なら内部と判定されます。

// vector<polygon> m_poly[]	ポリゴンのvector
bool isInner(float x, float y, float z){
    coord p(x,y,z);
    coord ray(1,0,0);
    int cnt = 0;
    for(int i=0; i<m_num; i++){                   
 	   if(m_poly[i].isCross(p,ray)) cnt++;
    }
    if(cnt%2==0) return false;
    else return true;
}

これらのコードによってStanford Bunnyを点群化した結果がこちら。

高速化

　上記コードには少し問題点があります。それは、全ポリゴンと交差判定を行うため、計算時間が非常にかかることです。軽いポリゴンデータを扱う際や点群数がそれほど必要ない場合は問題ありませんが、複雑な形状の点群化には対応できません。計算速度高速化の工夫が必要になります。ここでは個人的に考えた高速化方法について説明します。私は当分野について完全に素人なので、おそらくこの方法が最速ではありません。ご注意ください。

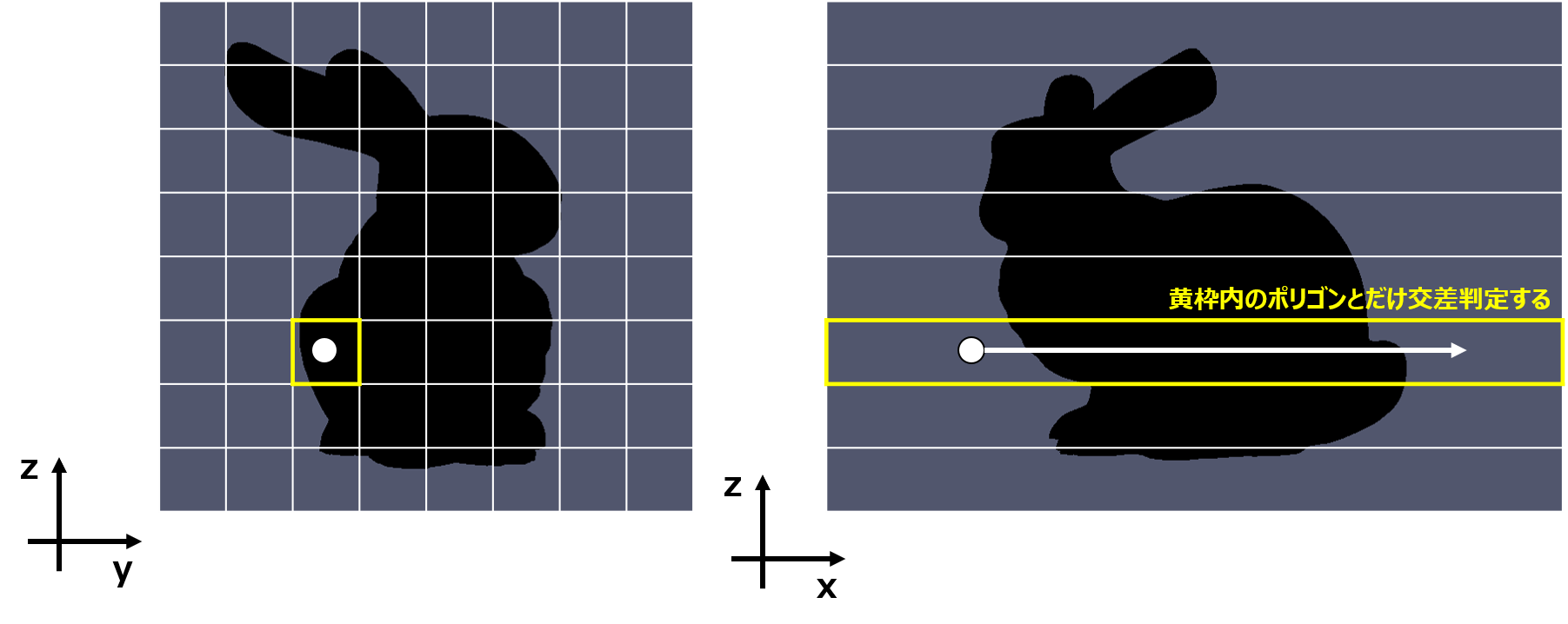
こちらを参考に、レイトレーシングでよく用いられるユニフォームグリッド型の空間分割を応用した方法を考えました。基本的な考え方は、どう考えてもレイの延長線に存在しないポリゴンは計算から省くことです。今回はx軸方向にレイを飛ばしているので、yz平面を格子状に分割し、レイの始点が含まれるグリッドに含まれるポリゴンとのみ交差判定をすれば良いです。

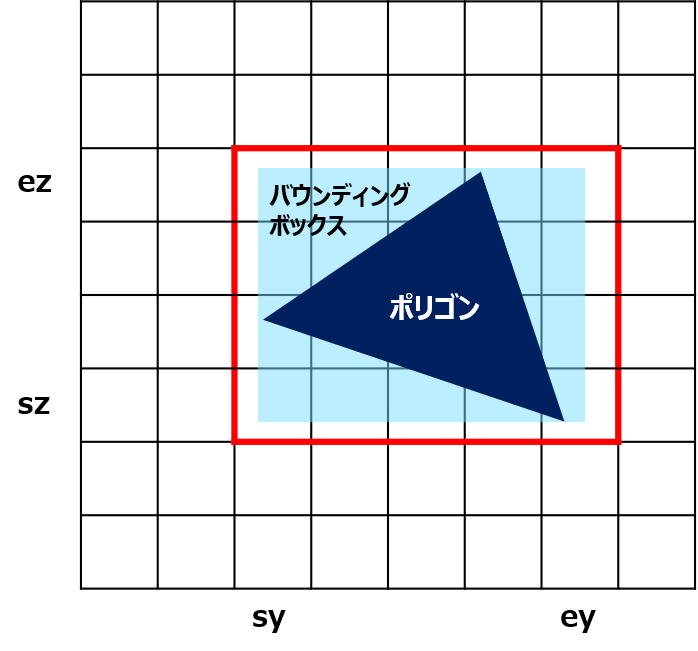
ポリゴンがグリッドに含まれるか否かは、ポリゴンのバウンディングボックスを生成することで容易に求められます。バウンディングボックスとは、あるオブジェクトを囲む直方体（2次元なら長方形）を意味します。バウンディングボックスの最小座標と最大座標が含まれるグリッド(sy,sz)及び(ey,ez)を求めれば、ポリゴンが含まれるグリッド(iy,iz)はsy<=iy<=ey、sz<=iz<=ezを満たします。

全ポリゴンに対して交差判定を行う場合と、上記アルゴリズムによる計算時間を比較します。対象となる3Dデータのポリゴン数は86,632、点群数は1,957です。

	計算時間 [ms]
改良前	114,827
改良後	334

空間の分割により、343倍の高速化に成功しました。

まとめ

　stlファイルを読みこんで、Crossing Number Algorithmによって点群化しました。ポリゴンとの交差判定にはTomas Mollerの交差判定アルゴリズムを用い、更にユニフォームグリッド型の空間分割を適用することで計算の高速化を行いました。もっと速くする方法があれば教えてください。以上、ご参考になれば幸いです！

Appendix（ソースコード）

#ifndef STL2POINTS_HPP
#define STL2POINTS_HPP
#include <iostream>
#include <fstream>
#include <vector>

namespace stl2points{

    // 座標
    struct coord{
        float x,y,z;
        coord():x(0),y(0),z(0){}
        coord(float a):x(a),y(a),z(a){}
        coord(float x_,float y_,float z_):x(x_),y(y_),z(z_){}
        void set(float a){
            x = a;
            y = a;
            z = a;
        }
        void set(float x_,float y_,float z_){
            x = x_;
            y = y_;
            z = z_;
        }
        coord operator+(coord other){
            coord res;
            res.x = this->x+other.x;
            res.y = this->y+other.y;
            res.z = this->z+other.z;
            return res;
        }
        coord operator-(coord other){
            coord res;
            res.x = this->x-other.x;
            res.y = this->y-other.y;
            res.z = this->z-other.z;
            return res;
        }
        coord operator+(float a){
            coord res;
            res.x = this->x+a;
            res.y = this->y+a;
            res.z = this->z+a;
            return res;
        }
        coord operator-(float a){
            coord res;
            res.x = this->x-a;
            res.y = this->y-a;
            res.z = this->z-a;
            return res;
        }
        coord operator*(float a){
            coord res;
            res.x = this->x*a;
            res.y = this->y*a;
            res.z = this->z*a;
            return res;
        }
        coord operator/(float a){
            coord res;
            res.x = this->x/a;
            res.y = this->y/a;
            res.z = this->z/a;
            return res;
        }
        float dot(coord other){
            return this->x*other.x+this->y*other.y+this->z*other.z;
        }
        coord outer(coord other){
            coord res;
            res.x = this->y*other.z-this->z*other.y;
            res.y = this->z*other.x-this->x*other.z;
            res.z = this->x*other.y-this->y*other.x;
            return res;
        }
    };

    inline float det(coord a, coord b, coord c){
        return ((a.x * b.y * c.z) + (a.y * b.z * c.x) + (a.z * b.x * c.y)
                - (a.x * b.z * c.y) - (a.y * b.x * c.z) - (a.z * b.y * c.x));
    }

    // ボックス
    struct box{
            coord min_pos,max_pos;
            box()=default;
            box(coord min_pos_, coord max_pos_){
                set(min_pos_,max_pos_);
            }
            void set(coord min_pos_, coord max_pos_){
                min_pos = min_pos_;
                max_pos = max_pos_;
            }
    };

    // ポリゴン
    struct polygon{
        coord v[3];
        coord normal;
        box bounding_box;
        void set(coord v0_, coord v1_, coord v2_, coord normal_){
            v[0] = v0_ ;
            v[1] = v1_ ;
            v[2] = v2_ ;
            normal = normal_;
            coord min_pos(1e+32),max_pos(-1e+32);
            for(int i=0; i<3; i++){
                min_pos.x = std::min(min_pos.x,v[i].x);
                min_pos.y = std::min(min_pos.y,v[i].y);
                min_pos.z = std::min(min_pos.z,v[i].z);
                max_pos.x = std::max(max_pos.x,v[i].x);
                max_pos.y = std::max(max_pos.y,v[i].y);
                max_pos.z = std::max(max_pos.z,v[i].z);  
            }
            bounding_box.set(min_pos,max_pos);     
        }
        bool isCross(coord p, coord ray){
            coord inv_ray = ray*(-1);
            coord edge1 = v[1]-v[0];
            coord edge2 = v[2]-v[0];
            float denominator = det(edge1,edge2,inv_ray);
            if(denominator==0) return false;
            coord d = p-v[0];
            float u = det(d,edge2,inv_ray)/denominator;
            if(u<0||1<u) return false;
            float v = det(edge1,d,inv_ray)/denominator;
            if(v<0||1<u+v) return false;
            float t = det(edge1,edge2,d)/denominator;
            if(t<0) return false;
            return true;
        }   
    };

    class object3d{
        private:
            std::vector<polygon> m_poly;
            int m_num;
            coord m_min_pos, m_max_pos;
            coord m_len, m_center;
            std::vector<std::vector<std::vector<polygon*>>> raybucket;
            bool isInner2(float x, float y, float z, float dl, float margin, coord ray, std::string &plane){
                coord p(x,y,z);
                coord region_min = m_center - m_len*margin/2 - dl*0.5;
                coord region_max = m_center + m_len*margin/2 + dl*0.5;
                int ix = (p.x - region_min.x)/dl;
                int iy = (p.y - region_min.y)/dl;
                int iz = (p.z - region_min.z)/dl;
                int cnt = 0;
                if(plane=="xy"){
                    for(int i=0; i<raybucket[ix][iy].size(); i++){                   
                        if(raybucket[ix][iy][i]->isCross(p,ray)) cnt++;
                    }
                }else if(plane=="yz"){
                    for(int i=0; i<raybucket[iy][iz].size(); i++){                   
                        if(raybucket[iy][iz][i]->isCross(p,ray)) cnt++;
                    }
                }else if(plane=="xz"){
                    for(int i=0; i<raybucket[ix][iz].size(); i++){                   
                        if(raybucket[ix][iz][i]->isCross(p,ray)) cnt++;
                    }
                }else{
                    std::cout << "!!! stl2sdf::object3d::isInner2 error" << std::endl;                    
                }
                if(cnt%2==0) return false;
                else return true;
            }
            bool split_raybucket(float dl, float margin, std::string &plane){
                coord region_min = m_center - m_len*margin/2 - dl*0.5;
                coord region_max = m_center + m_len*margin/2 + dl*0.5;
                coord region_m_len = region_max - region_min;
                int nx = region_m_len.x/dl + 1;
                int ny = region_m_len.y/dl + 1;
                int nz = region_m_len.z/dl + 1;
                std::vector<std::vector<std::vector<polygon*>>>().swap(raybucket);
                if(plane=="xy"){
                    raybucket.resize(nx);
                    for(int ix=0; ix<nx; ix++) raybucket[ix].resize(ny);
                    for(int i=0; i<m_num; i++){
                        int sx = (m_poly[i].bounding_box.min_pos.x - region_min.x)/dl;
                        int sy = (m_poly[i].bounding_box.min_pos.y - region_min.y)/dl;
                        int ex = (m_poly[i].bounding_box.max_pos.x - region_min.x)/dl;
                        int ey = (m_poly[i].bounding_box.max_pos.y - region_min.y)/dl;
                        for(int ix=sx; ix<=ex; ix++){
                            for(int iy=sy; iy<=ey; iy++){
                                raybucket[ix][iy].push_back(&m_poly[i]);
                            }
                        }
                    }
                }else if(plane=="yz"){
                    raybucket.resize(ny);
                    for(int iy=0; iy<ny; iy++) raybucket[iy].resize(nz);
                    for(int i=0; i<m_num; i++){
                        int sy = (m_poly[i].bounding_box.min_pos.y - region_min.y)/dl;
                        int sz = (m_poly[i].bounding_box.min_pos.z - region_min.z)/dl;
                        int ey = (m_poly[i].bounding_box.max_pos.y - region_min.y)/dl;
                        int ez = (m_poly[i].bounding_box.max_pos.z - region_min.z)/dl;
                        for(int iy=sy; iy<=ey; iy++){
                            for(int iz=sz; iz<=ez; iz++){
                                raybucket[iy][iz].push_back(&m_poly[i]);
                            }
                        }
                    }
                }else if(plane=="xz"){
                    raybucket.resize(nx);
                    for(int ix=0; ix<nx; ix++) raybucket[ix].resize(nz);
                    for(int i=0; i<m_num; i++){
                        int sx = (m_poly[i].bounding_box.min_pos.x - region_min.x)/dl;
                        int sz = (m_poly[i].bounding_box.min_pos.z - region_min.z)/dl;
                        int ex = (m_poly[i].bounding_box.max_pos.x - region_min.x)/dl;
                        int ez = (m_poly[i].bounding_box.max_pos.z - region_min.z)/dl;
                        for(int ix=sx; ix<=ex; ix++){
                            for(int iz=sz; iz<=ez; iz++){
                                raybucket[ix][iz].push_back(&m_poly[i]);
                            }
                        }
                    }
                }else{
                    std::cout << "!!! stl2sdf::object3d::split_raybucket error" << std::endl;
                    return false;
                }
                return true;
            }
        public:
            object3d()=default;
            object3d(const char* file_name, float margin=1.2){
                set(file_name,margin);
            }
            int num_polygons(){
                return m_num;
            }
            coord min_pos(){
                return m_min_pos;
            }
            coord max_pos(){
                return m_max_pos;
            }
            coord len(){
                return m_len;
            }
            coord center(){
                return m_center;
            }
            bool set(const char* file_name, float margin){
                // ファイルオープン
                std::ifstream fin( file_name, std::ios::in | std::ios::binary );
                if(!fin) return false;

                // ポリゴン数の読み込み
                fin.seekg(80,std::ios_base::beg);
                fin.read((char*) &m_num, sizeof(int) );

                // 各ポリゴンの法線と座標の読み込み
                m_poly.resize(m_num);
                for(int i=0; i<m_num; i++){
                    coord vbuff[3];
                    coord nbuff;
                    fin.read((char*) &nbuff, sizeof(coord));
                    for(int j=0; j<3; j++){
                        fin.read((char*) &vbuff[j], sizeof(coord));
                    }
                    m_poly[i].set(vbuff[0],vbuff[1],vbuff[2],nbuff);
                    fin.seekg(2,std::ios_base::cur);
                }
                fin.close();

                // 最小、最大座標の計算
                m_min_pos.set(1e+32);
                m_max_pos.set(-1e+32);
                for(int i=0; i<m_num; i++){
                    for(int j=0; j<3; j++){
                        m_min_pos.x = std::min(m_min_pos.x,m_poly[i].v[j].x);
                        m_min_pos.y = std::min(m_min_pos.y,m_poly[i].v[j].y);
                        m_min_pos.z = std::min(m_min_pos.z,m_poly[i].v[j].z);
                        m_max_pos.x = std::max(m_max_pos.x,m_poly[i].v[j].x);
                        m_max_pos.y = std::max(m_max_pos.y,m_poly[i].v[j].y);
                        m_max_pos.z = std::max(m_max_pos.z,m_poly[i].v[j].z);
                    }
                    
                }
                m_len = max_pos() - min_pos();
                m_center = (max_pos() + min_pos())*0.5;
                return true;  
            }
            bool isInner(float x, float y, float z){
                coord p(x,y,z);
                coord ray(1,0,0);
                int cnt = 0;
                for(int i=0; i<m_num; i++){                   
                    if(m_poly[i].isCross(p,ray)) cnt++;
                }
                if(cnt%2==0) return false;
                else return true;
            }

            bool output_point_cloud(float dl, float margin, const char* file_name){
                coord region_min = m_center - m_len*margin/2;
                coord region_max = m_center + m_len*margin/2;
                std::ofstream fout(file_name);
                fout << "x,y,z" << std::endl;
                for(float x=region_min.x; x<region_max.x; x+=dl){
                    for(float y=region_min.y; y<region_max.y; y+=dl){
                        for(float z=region_min.z; z<region_max.z; z+=dl){
                            if(isInner(x,y,z)) fout << x << "," << y << "," << z << std::endl;
                        }
                    }
                }
                fout.close();                
            }
            bool output_point_cloud_fast(float dl, float margin, const char* file_name){
                coord region_min = m_center - m_len*margin/2;
                coord region_max = m_center + m_len*margin/2;
                std::string plane;
                if(m_len.x<=m_len.y&&m_len.x<=m_len.z) plane = "yz";
                if(m_len.y<=m_len.x&&m_len.y<=m_len.z) plane = "xz";
                if(m_len.z<=m_len.x&&m_len.x<=m_len.y) plane = "xy";
                coord ray;
                if(plane=="xy") ray.set(0,0,1);
                else if(plane=="yz") ray.set(1,0,0);
                else if(plane=="xz") ray.set(0,1,0);
                else std::cout << "!!! stl2sdf::object3d::output_point_cloud2 error" << std::endl;        
                split_raybucket(dl,margin,plane);      
                std::ofstream fout(file_name);
                fout << "x,y,z" << std::endl;
                for(float x=region_min.x; x<region_max.x; x+=dl){
                    for(float y=region_min.y; y<region_max.y; y+=dl){
                        for(float z=region_min.z; z<region_max.z; z+=dl){
                            if(isInner2(x,y,z,dl,margin,ray,plane)) fout << x << "," << y << "," << z << std::endl;
                        }
                    }
                }
                fout.close();  
            }
    };

}


#endif