はじめに
書籍『Pythonで体験するベイズ推論 PyMCによるMCMC入門』が届いて、喜びつつ手を動かしながら進めてみたはいいものの、理解できそうだけどあとひとつ、という状況だったので自分の基礎的な理解を確認するためにも記事としてまとめてみました。
自分も初学者ではありますが、これからベイズ流アプローチを体験したい方のサポートになれば幸いです。
まずはコインの確率分布について確認した後、PyMCから算出される事後分布を確認して、その後にベイズ統計における'主観'をどう取り入れることができるのか試していきます。
コイン投げの分布
まずはコインをN回投げたときの表の回数をH(Head)とすると裏の回数は N - H となります。
wikipediaの二項分布を読むと、今回のコイン投げの課題はこの二項分布(Binomial Distribution)に従うと言えそうです。
また、この二項分布は分布の形状を決めるパラメータpとNがあります。
pは求めたいパラメータで、Nはコインの試行回数がそのまま使えます。
真正なコインであれば裏も表も出る確率が一緒ということがわかっているため、私たちはp=0.5であることを知っているという特殊な状況ですが、これを知らないからpの値を推定するのだと今のところは思って下さい(p=0.5のときもっとも表と裏の出る確率はちょうど半分になる)。
...でも本当にp=0.5という認識だけでいいのでしょうか?
私達がすぐに頭の中でやることといえば、表と裏が半分ずつの確率になるはずだから p=0.5 に違いない!というものですが、この考え方は不確実さを捨ててしまっています。
例えば次のグラフを確認するとどちらもp=0.5あたりで最大であることに変わりありませんが、p=0.5と言える確信が違ってくるという風に解釈することはできませんか?
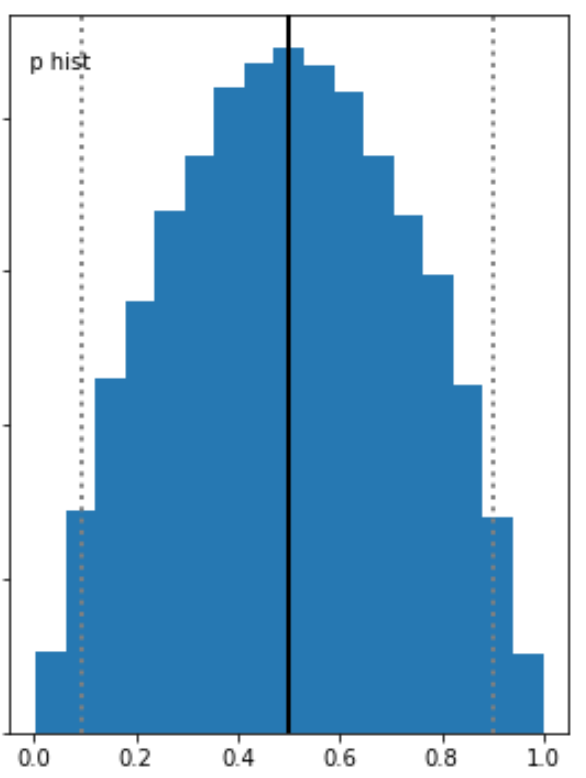
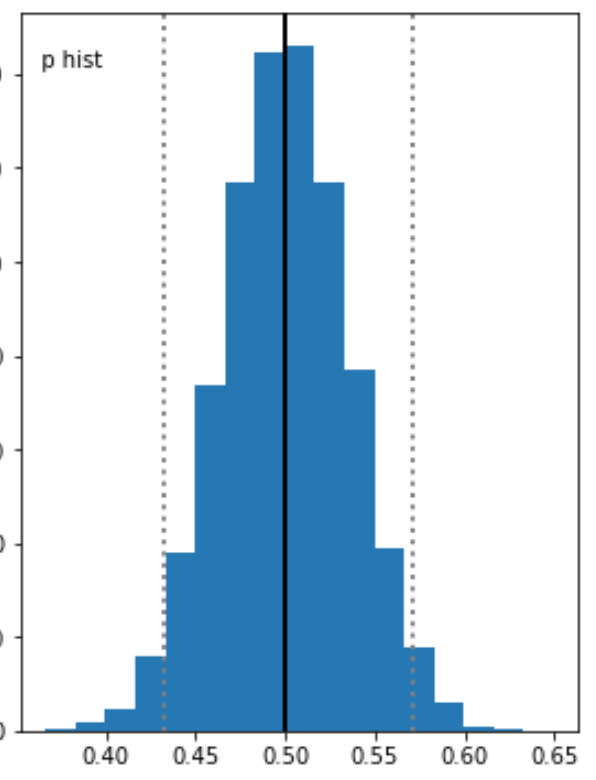
上の図は下の図に比べて相対的に青色の領域が左右に伸びています。
これは上の図のp=0.5あたりの確信度は、下の図のp=0.5あたりの確信度に比べて低いということを表しています。
言い換えると下の図の方がより自信を持ってp=0.5あたりだよ!と主張しているといえます。
このようにベイズのアプローチでは特定の値として扱うのではなく、不確実性を表現できるもっと柔らかい形(確率分布)で扱います。
p=0.5という情報だけでなく、p=0.1なのがこれくらい、p=2なのがこれくらいp=3なのが...というような形式ということですね。
MCMC
本記事ではMCMCと呼ばれる手法を使います。
MCMCに関しては検索エンジンで優れた情報源がたくさん見つかるので、別途参照してみて下さい。
ひとまずは確率分布を求めることができる手法の一つと思っていただければ大丈夫です。
特徴としては厳密な事後分布の形状を求めることはせずに、それに近い結果を出力することができる手法になります。
複雑な事後分布ですと、厳密な分布の形状を求めることがそもそも不可能な場合もありますが、MCMCを使うことで現実的な計算時間で分布を求めることができます。
実は今回の内容だと求める分布の形状が簡単であることがわかっているためMCMCである必要はないのですが、実際の応用の場面では分布の形状自体がどうなっているかわからない場合が多いため、そのエッセンスを体験することも念頭にMCMCを活用して進めることにしました。
主観をなくした状態で事後分布を見る
今回は事後分布を求めるのにpymcというMCMCの実装の一つを使います。
import pymc as pm
from pymc.Matplot import plot as mcplot
まず最初に何のデータも観測していない状態を確認します。
加えて、このコインが表か裏のどちらかが出やすいとは思っていないという状況です。
observed = []
h = observed.count(1)
n = len(observed)
# 二項分布のパラメータpの事前分布(一様分布を設定)
alpha, beta = 1, 1
p = pm.Beta('p', alpha=alpha, beta=beta)
# コイン投げの試行は二項分布に従うのでBinomial
obs = pm.Binomial('y', n=n, p=p, value=h, observed=True)
# モデルを定義してサンプリングすることで事後分布を求める
model = pm.Model([obs, p])
mcmc = pm.MCMC(model)
mcmc.sample(60000, 10000)
mcplot(mcmc.trace('p'))
observed = []が実際にコイン投げで観測された表と裏のリストになります。
今後このobservedを変更することで分布の形状がどう変化するかを確認していきます。
pm.Beta('p', alpha=alpha, beta=beta)が'このコインが表か裏のどちらかが出やすいとは思っていない'という情報を反映しています。
書籍などでは'仮定を置かないため一様分布を事前分布に設定する'などと表現される場合が多いです。
その後モデルを定義してサンプリングを行い、事後分布の形状を求めます。
sample(60000, 10000)では6万のサンプルを集め、最初の1万を破棄することを指定しています。
興味のある方はMCMC自体を調べてみて下さい。
最後に私達の興味のあった二項分布のパラメータpのサンプルを集計し、分布として出力しています。
上を実行して何秒か待つと、次のような図が出力されます。
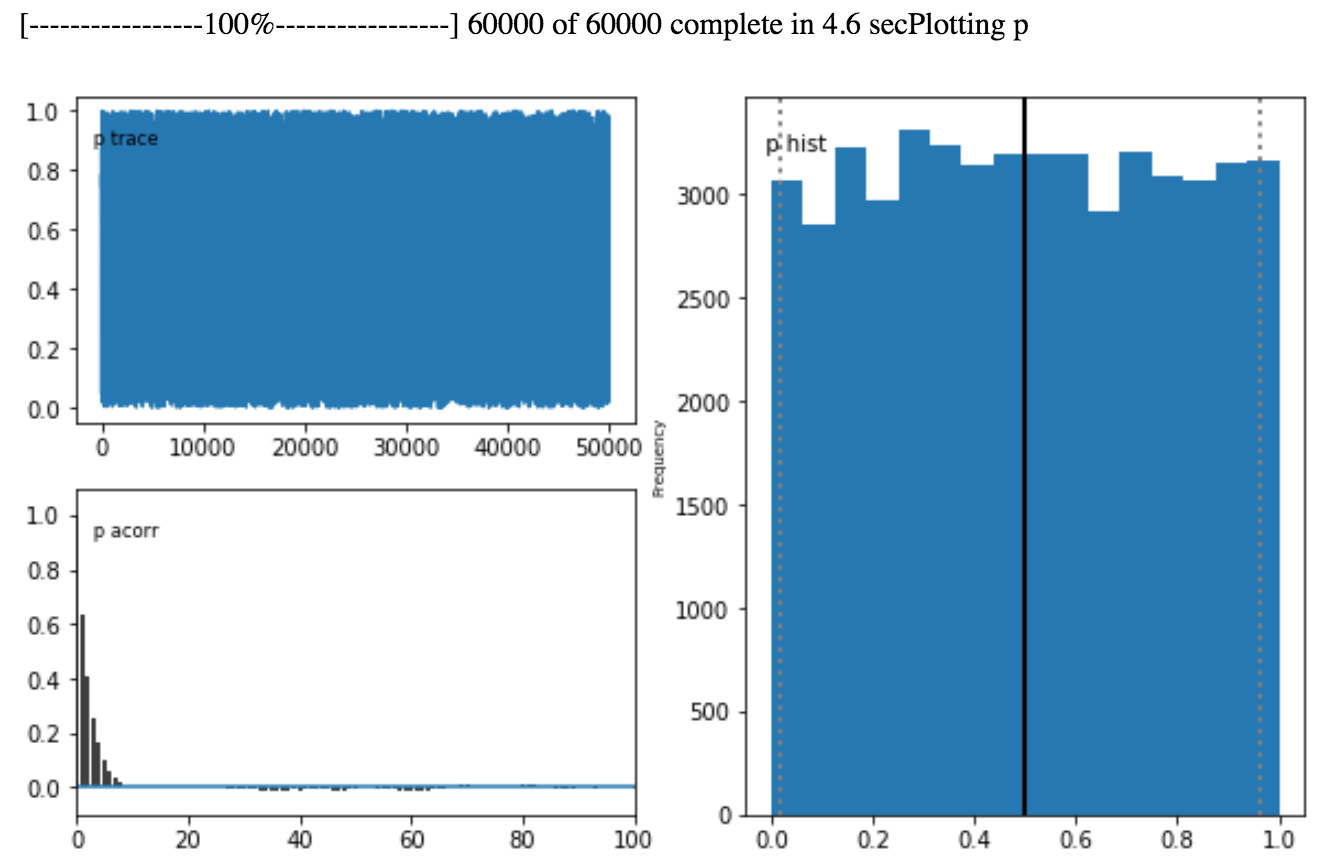
右の図が事後分布の形状を示しています。
理想的にはwikipedia:連続一様分布の図にあるような形状になるのですが、MCMCは近似的な出力ですので、いくらかばらつきが出てきます。
上記の例だとなにもデータを観測していないため、なにも仮定を置いていない情報がそのまま出てきたことになります。
次にコイン投げを1回行って裏(=0)がでたときの形状を確認してみます。
observed = [0]として上記のコードを再度実行すると次のような図が出力されます。

ずいぶんと形状が変わりました。
この結果は、このコインは裏が出やすいぞ!ということを表現しています。
次にもう一度裏が出た場合を確認します(observed = [0, 0])。

observed = [0]の分布形状と比較すると0.1が伸びてそれ以外がなだらかに小さくなりました。
なにせ2回連続で裏がでたのですから、observed = [0]と比較するとより自信を持って裏のほうがでやすい!といえるという信念を反映しているといえます。
次に表が出た場合です(observed = [0, 0, 1])。
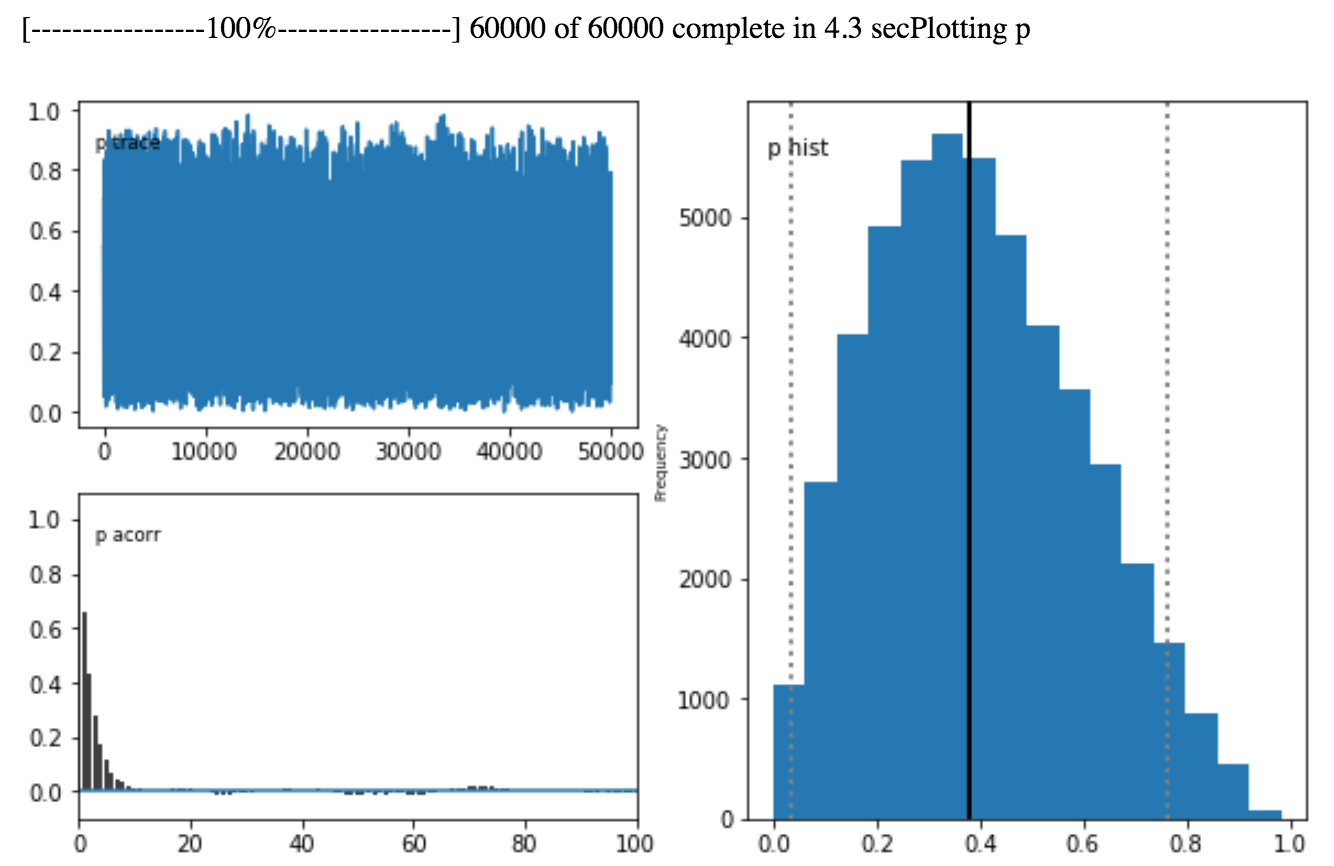
今までとは違って山のようなものが確認でき、その頂がやや右側に寄っていることが確認できます。
今までとは違って、表も観測できたため、pの値も表が出やすいように更新されています。
もっとコインを投げてみましょう。
コインを50回コインを投げて表が24回の時の事後分布を確認します。
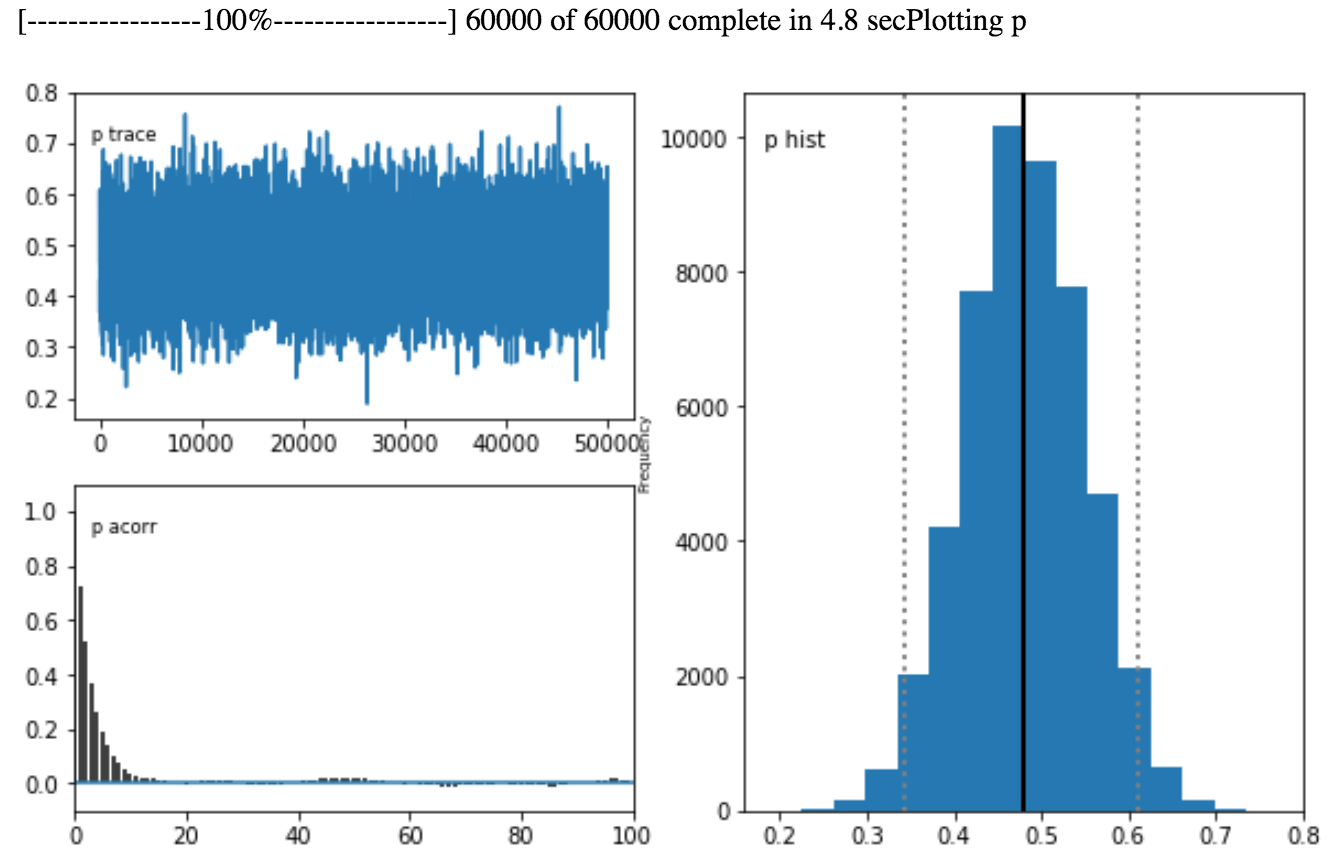
山の頂点がほぼほぼp=0.5に近づき、私達がp=0.5だろうと思っていた予想と似てきましたね。
でもベイズではp=0.5という点ではなく、確率分布で情報を保持していることは忘れないようにしましょう。
イカサマかもしれないと思って事後分布を見る
コイン投げを行い、表が出たら相手が勝ち、裏なら自分が勝つというシンプルなゲームがあったとします。
コインは相手が持参してきたため、あなたはそのコインを怪しんでいます。
この怪しんでいるという主観をモデルに取り込んでみます。
前の例だと主観がない状態で一様分布( beta(1,1) )を設定しましたが、これを相手にとって有利な表が出やすいという風に確率分布で表現します。
例えば次のようにしてみます。
observed = []
alpha, beta = 2, 0.5
p = pm.Beta('p', alpha=alpha, beta=beta)
このとき、次の図のように表現されていることがわかります。

...めちゃくちゃ疑ってますね!
ここから試しにコインを投げさせてもらうことで、分布がどう変化するか観測してみます。
ほら、表がでた!
observed = [1]の場合

先程の図とほとんど変化がありません。
一方で、微弱ではありますが表が出やすいという信念が強まりました。
あれ、裏が出た!
observed = [0]の場合

信念に反して裏が出ました。
これは、ひょっとすると細工されてないかもしれない?、ということを表現しています。
もっとコイン投げ
50回投げて24回表、26回裏(observed = [1]*24 + [0]*26)になった場合、次のような分布になります。

これまでに似たような分布をみたことがある気がします。
この記事の前半で主観なしでコインを50回振って24回表26回裏の結果をだしました。
はじめは疑っていたとしても50回も投げさせてもらったらこの2つの分布の形状はとても似てきました。
どんなに思い込みが強くても、試行回数が多ければその差はなくなってくることが分かってきたかと思います。
今回はここまでにしますが、もしチェックのために3回までなら試しにコイン投げをしてもいいよと言われた状況で、それぞれがどの程度のチップを賭けるかという期待値まで絡めてくると、より面白い事例になりそうですね。
さいごに
本記事よりも複雑かつ興味深い事例ははじめにで紹介したように書籍『Pythonで体験するベイズ推論 PyMCによるMCMC入門』で扱っているため、興味を持った方は一読してみるのがおすすめです。
自分でも何か思いついたら何か書いてみようかと思います。