1. 標準正規分布とは
平均μ=0, 分散σ=1の正規分布、
すなわち以下の数式で表される関数のことです。
f(x) = \frac{1}{ \sqrt{2 \pi } } e^{- \frac{x^2}{2} }
2. 自分で標準正規分布を作成
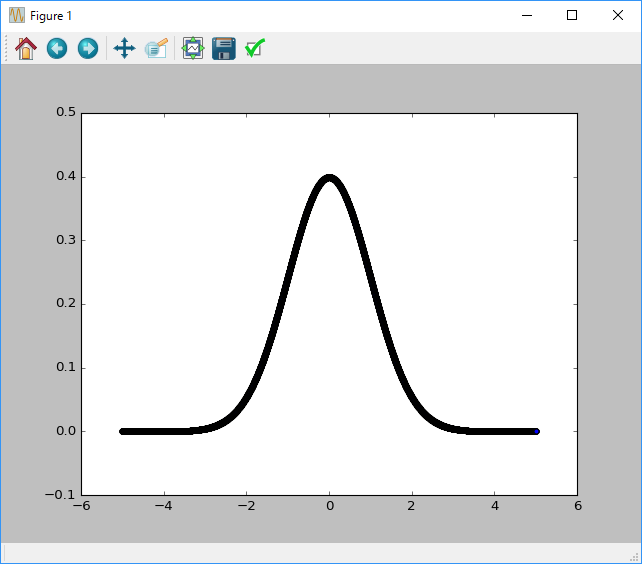
前述のf(x)を自分で定義して、試しに [-5.0, -4.999, -4.998, ... , 4.998, 4.999, 5.0] と~5.0 ~ 5.0の数列を入れてみると、
一般に正規分布と呼ばれる形のグラフが得られます。
# coding: utf-8
import numpy as np
import math
# f(x)を自分で書く
f = lambda x: (math.exp(-x**2/2)) / math.sqrt(2*math.pi)
# ベクトルxを [-5.0, ..., 5.0] の区間で作成
n = np.linspace(-5.0, 5.0, 10000)
# f(x)の結果を得る
p = []
for i in range(len(n)):
p.append(f(n[i]))
# グラフに表示
plt.scatter(n, p)
plt.show()
綺麗な釣り鐘が得られましたが、一々自分で定義していくのは、少し面倒くさいです。
何より平均や分散を変えたくなった時に、手間がかかります。
3. scipyを使用
scipy.statsモジュールを利用すると、
上のコード(norm_original.py)ではラムダ式で定義した数式を、関数から呼び出すことができます。
# coding: utf-8
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
# ベクトルxを [-5.0, ..., 5.0] の区間で作成
n = np.linspace(-5.0, 5.0, 10000)
# 平均0, 標準偏差1の正規分布における、xの確率を求める
p = []
for i in range(len(n)):
p.append(norm.pdf(x=n[i], loc=0, scale=1))
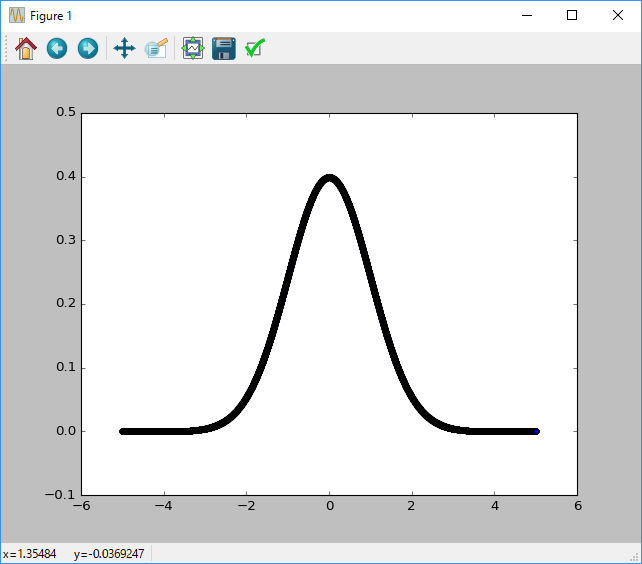
# 乱数-確率 の特性を散布図で表し、標準正規分布のグラフを作成
plt.scatter(n, p)
plt.show()
こちらは引数で平均と分散を指定できるので、簡単に違う形の正規分布を得ることが出来ます。
4. 累積分布関数から同時エントロピーを見てみる
前の章では、scipy.stats.norm.pdfから正規分布の確率密度関数を使いました。
今度は少しだけいじって、scipy.stats.norm.cdfから正規分布の累積分布関数を使ってみます。
Wikipediaの結合エントロピーの記述を参考に書いていきます。
同時エントロピー(結合エントロピー)H(X)は、確率変数Xの値の不確かさを表しています。
Xに属するイベントxが発生する確率がp(x)であるとき、Xのエントロピーは、
H(X) = - \sum_{x} p_x log_2 (p_x)
で表されます。
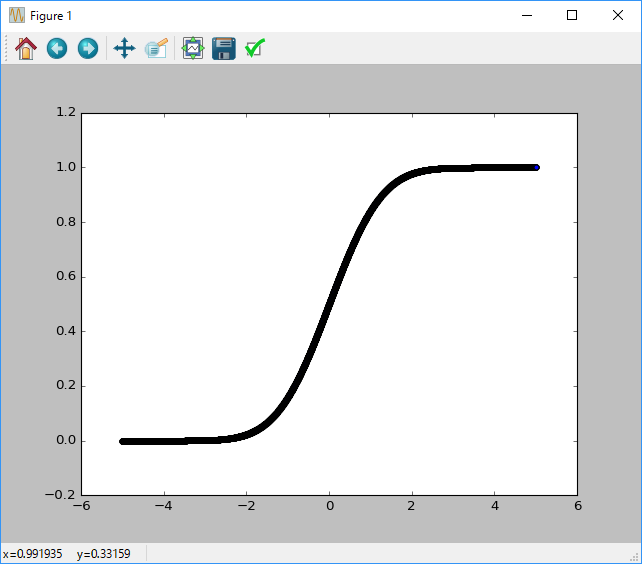
ここでは確率が標準正規分布に乗ると考えて、エントロピーをグラフに表すと、
---p.append(norm.pdf(x=n[i], loc=0, scale=1))
+++p.append(norm.cdf(x=n[i], loc=0, scale=1))
このようなH(X)が得られます。