今回は熱伝導方程式
$$
\frac{K_0}{c \rho} \frac{\partial^2 u}{\partial x^2} + \frac{Q}{c \rho} = \frac{\partial u}{\partial t}
$$
を導出してみます.これは,固体の物質の中を熱がどのように伝わるかを微分方程式で表したものです.
この微分方程式を解くと,
- 物質のどこの温度が高くて,どこの温度が低いのか
- 物質中をどのように温度が伝わっていくか
を表した関数$u(x, t)$を得られます.
しかし,解くところまでやると大変なので,今回は方程式を導出するところまでにしておきます.
ここでは熱量と熱エネルギーを同じ意味の言葉として使っていきますが,細かいところに関しては大目に見てください.
ではさっそく熱伝導方程式を導出してみましょう.
熱伝導方程式の導出
熱伝導方程式はよく時刻$t$,3次元空間座標$(x, y, z)$の関数で表されるのですが,3次元空間での式をいきなり導出するのは少し大変です.
1次元空間における$x$と$t$についての方程式さえ導いてしまえば容易に3次元に拡張できるので,今回は1次元の熱伝導方程式のみを導出します.
1次元の熱伝導方程式を導出するために,直方体の形をした密度が均一な物質を考えます.
この物質の温度は時刻$t$と$x$座標の値のみによって変化するとします.つまり,どの$x$について物質を輪切りにしても,その断面の温度は均一であるとします.
また,物質の側面からの熱の出入りも無いものとします.

この物質の$[x,x+\Delta x]$の区間に注目して1次元の熱伝導方程式を立てていきます.
熱伝導方程式は次の2つの法則から導かれます.
- エネルギー保存の法則
- フーリエの法則
まずはエネルギー保存の法則から見ていきましょう.
エネルギー保存の法則 (熱量の保存)
エネルギー保存の法則は次のようなものです.
$E_{in}$ $\Delta t$秒間に物質外部から与えられられる熱エネルギーの総和
$E_{out}$ $\Delta t$秒間に物質内部から外に出て行く熱エネルギーの総和
$E_{g}$ $\Delta t$秒間に物質内部で熱以外のエネルギーが変換されて生じた熱エネルギーの総和
$\Delta E_{st}$ $\Delta t$秒間での物質内部に保存されている熱エネルギーの変化
とすると,
$$
E_{in} - E_{out} + E_{g} = \Delta E_{st}
$$
という式が成り立つ.1
式を見れば,当たり前のことを言っているだけということがわかっていただけると思います.
図で表すとこんな感じになります.

上の式のそれぞれの項を書き換えていくと熱伝導方程式を導くことができます.
物質内部に保存されている熱エネルギーの変化
まずは$\Delta E_{st}$を書き換えます.
位置$x$,時刻$t$における物質の温度を$u(x, t)$とします.
このとき,物質の区間$[x, x + \Delta x]$に保存されている熱エネルギーは次の式で表されます.
$$
c \rho A \Delta x u(x, t)
$$
$c$は物質の比熱,$\rho$は物質の密度,$A$は物質の断面積です.比熱と熱エネルギーの関係について復習したい方は「わかりやすい高校物理の部屋」を見るとよいです.
$\rho A \Delta x$が区間$[x, x + \Delta x]$の物質の質量を表していることを踏まえて式をよく見ると,たしかにこの式はエネルギーを表しています.
$\Delta t$秒間での熱エネルギーの変化は
$$
\Delta E_{st} = c \rho A \Delta x u(x, t+\Delta t) - c \rho A \Delta x u(x, t)
$$
となります.
物質の断面を通過する熱エネルギー
今度は
$E_{in}$ $\Delta t$秒間に物質外部から与えられられる熱エネルギーの総和
$E_{out}$ $\Delta t$秒間に物質内部から外に出て行く熱エネルギーの総和
を具体的なかたちに書き換えます.
ただし,$E_{in}$は$x$における断面から流れ込むエネルギー,$E_{out}$は$x+\Delta x$における断面から流れ出すエネルギーとします.
フーリエの法則
一般に,ある物質の$x$における断面を通過する熱量$q$は,熱伝導率$K_0$,断面積$A$,温度勾配$\frac{\partial u}{\partial x}\rvert_{x}$に比例することが知られています.これをフーリエの法則と言います.
$$
q = - K_0 A \frac{\partial u}{\partial x}\rvert_{x}
$$
$K_0$は物質に依存する熱の伝わりやすさの指標です.たとえば木材よりも金属のほうが熱が伝わりやすいので,熱伝導率は大きくなります.
次に,通過する熱量$q$が断面積$A$と温度勾配$\frac{\partial u}{\partial x}$に比例することを見てみます.
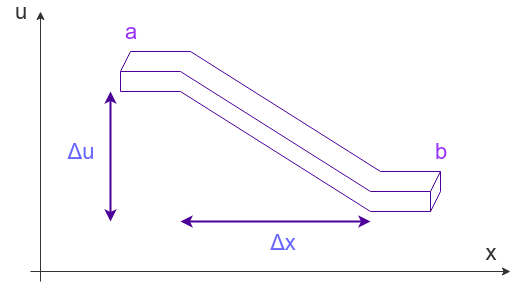
下の図のように,a地点からb地点に向かって水が流れるような水路を考えます.
単位時間あたりに流れる水の量は水路の断面積$A$と水路の傾き$\frac{\Delta u}{\Delta x}$に比例しますよね.
フーリエの法則はこの流れる水の量を熱量に置き換えたものです.
フーリエの法則の法則の式にマイナスがついているのは,水路の傾きと熱の伝わる方向が逆だからです.
この図ではa地点のほうが高いところにあるため,熱はa→bの方向に流れます.しかし水路の傾き$\frac{\Delta u}{\Delta x}$は負になっているため,これを打ち消すためにマイナスをかけています.
熱エネルギーが$x$から流れこみ,$x+\Delta x$から出て行くとすると,
$x$の断面を$\Delta t$秒間に通過する熱量の総和は
$$
E_{in} = - \Delta t K_0 A \frac{\partial u}{\partial x}\rvert_{x}
$$
$x+\Delta x$の断面を$\Delta t$秒間に通過する熱量の総和は
$$
E_{out} = - \Delta t K_0 A \frac{\partial u}{\partial x}\rvert_{x+\Delta x}
$$
となります.
物質内部でエネルギーが変換されて生じた熱エネルギーの総和
最後に$E_{g}$を書き換えます.
「物質内部で他のエネルギーが変換されて生じた熱エネルギー」というのは,たとえば電球のフィラメントのように電気エネルギーが変換されて生じる熱エネルギーや,化学反応における反応熱などのことを言います.
電球のフィラメントについて考えると,電流の大きさが一定であれば生じる熱の大きさはフィラメントの長さに比例しますよね.
化学反応によって生じる熱も,(反応が均一に起これば)その熱量は体積に比例するはずです.
ここでは熱伝導をモデル化する物質として均質なものを考えているため,物質のどこをとったとしても,体積が同じであれば生じる熱の大きさは一定であるとします.

単位体積の物質が単位時間あたりに発生する熱量を$Q$とすると,生じる熱量は体積と時間に比例します.
よって区間$[x, x+\Delta x]$において$\Delta t$秒間に発生する熱量は
$E_{g} = \Delta t \Delta x A Q$
となります.
熱伝導方程式
以上より
$E_{in} = - \Delta t K_0 A \frac{\partial u}{\partial x}\rvert_{x}$
$E_{out} = - \Delta t K_0 A \frac{\partial u}{\partial x}\rvert_{x+\Delta x}$
$E_{g} = \Delta t \Delta x A Q$
$\Delta E_{st} = c \rho A \Delta x u(x, t+\Delta t) - c \rho A \Delta x u(x, t)$
を導くことができました.ここまでくればあとは簡単です.あとはこれをエネルギー保存の法則
$$
E_{in} - E_{out} + E_{g} = \Delta E_{st}
$$
に当てはめていくだけです.
では実際にやってみましょう.
$$
(- \Delta t K_0 A \frac{\partial u}{\partial x}\rvert_{x}) - (- \Delta t K_0 A \frac{\partial u}{\partial x}\rvert_{x+\Delta x}) + \Delta t \Delta x A Q = c \rho A \Delta x u(x, t+\Delta t) - c \rho A \Delta x u(x, t)
$$
項をまとめます.
$$
\Delta t K_0 A (\frac{\partial u}{\partial x}\rvert_{x+\Delta x} - \frac{\partial u}{\partial x}\rvert_{x}) + \Delta t \Delta x A Q = c \rho A \Delta x \left[u(x, t+\Delta t) - u(x, t)\right] \
$$
両辺を$A c \rho \Delta t \Delta x$で割ります.
$$
\frac{K_0}{c \rho} \frac{\frac{\partial u}{\partial x}\rvert_{x+\Delta x} - \frac{\partial u}{\partial x}\rvert_{x}}{\Delta x} + \frac{Q}{c \rho} = \frac{u(x, t+\Delta t) - u(x, t)}{\Delta t}
$$
$\Delta x \rightarrow 0, \Delta t \rightarrow 0$とすると,
$$
\frac{K_0}{c \rho} \frac{\partial^2 u}{\partial x^2} + \frac{Q}{c \rho} = \frac{\partial u}{\partial t}
$$
となり,熱伝導方程式を導くことができました.
おわりに
気になる点や間違っている点,わかりにくかったところなどがあればおしえてください.
参考資料
-
厳密には$\Delta t$秒の間にもそれぞれの項は時間変化するため誤差項$\omicron(\Delta t)$が付け足されるべきですが,$\Delta t \rightarrow 0$としたとき$\omicron(\Delta t)$も$0$に収束するためここでは省略しています. ↩