Tomasi-Kanade法による3次元復元

こんにちは，いしたーです．最近はDeNAで3次元復元関連のアルバイトをしています．

今回は3次元復元の古典的な手法であるTomasi-Kanade法[1]の解説をしていきます．
コードはGitHubにあります．

Tomasi-Kanade法とは

2次元の画像の集合から3次元の物体を復元する手法です．

さっそくデモをお見せします．

これらはある3次元の点の集合を撮影(平面に投影)したものです．

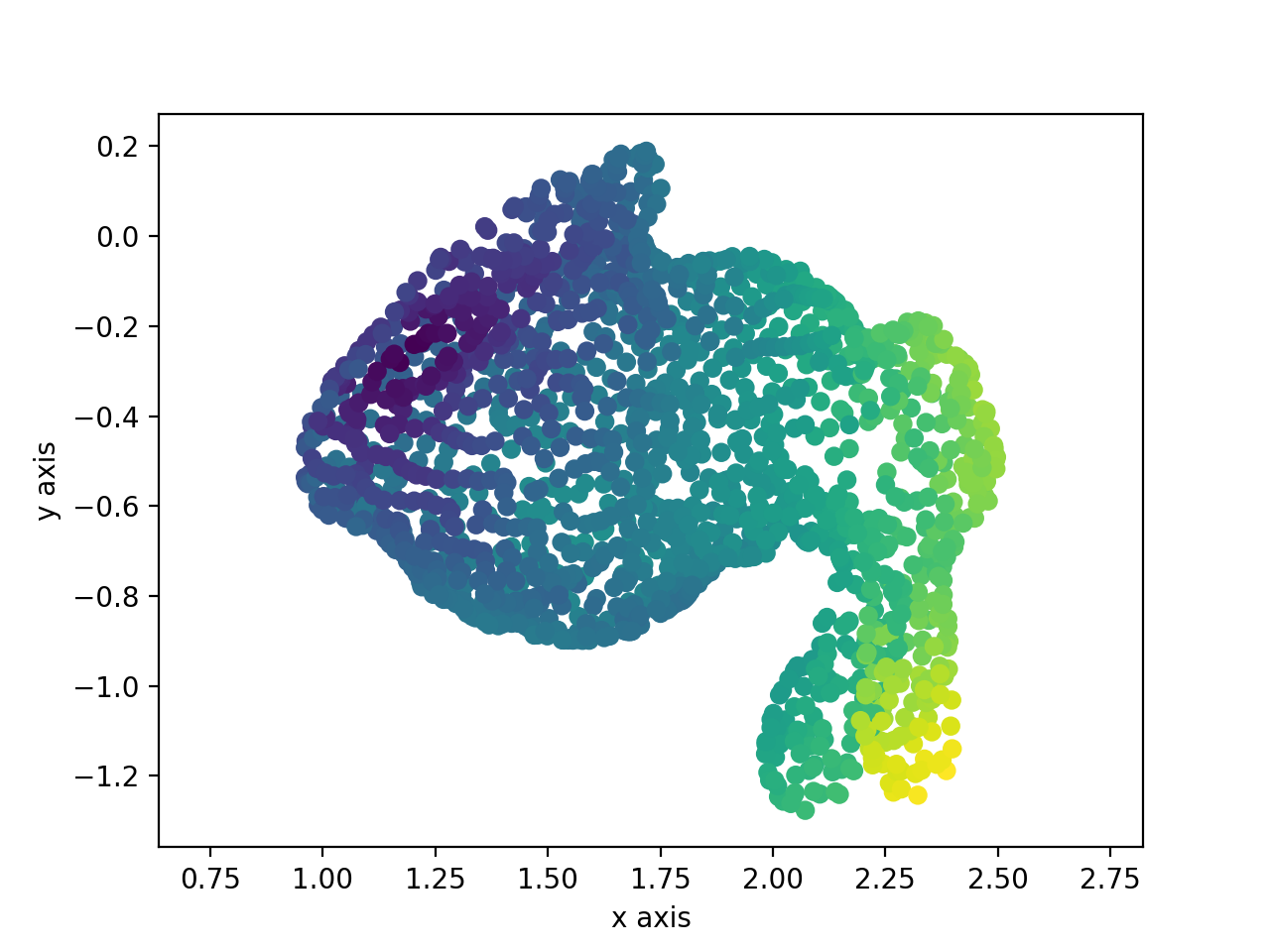
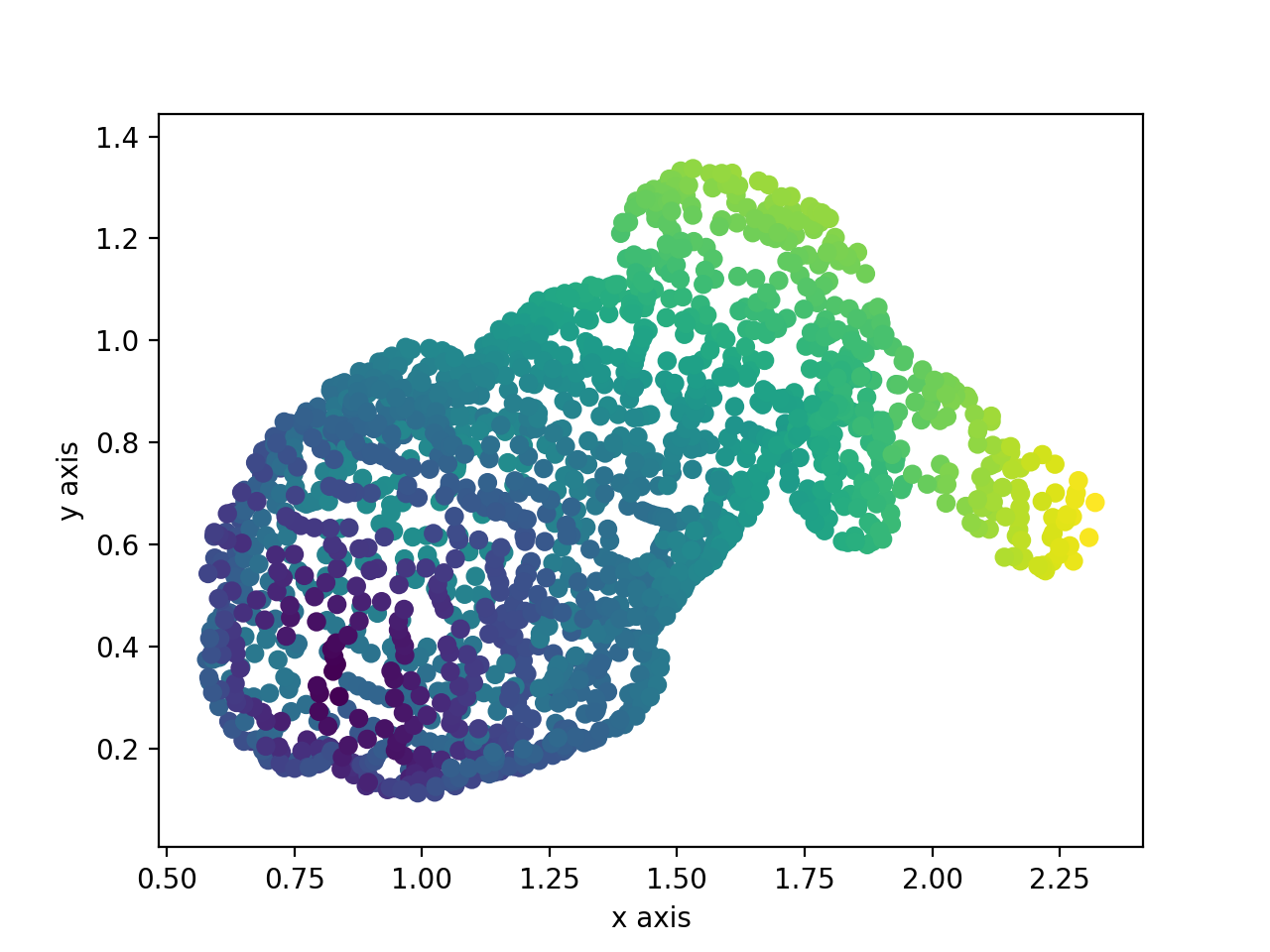
これらの画像をTomasi-Kanade法で処理すると，こんなふうにもとの3次元の点群を2次元の点群のみから復元することができます．

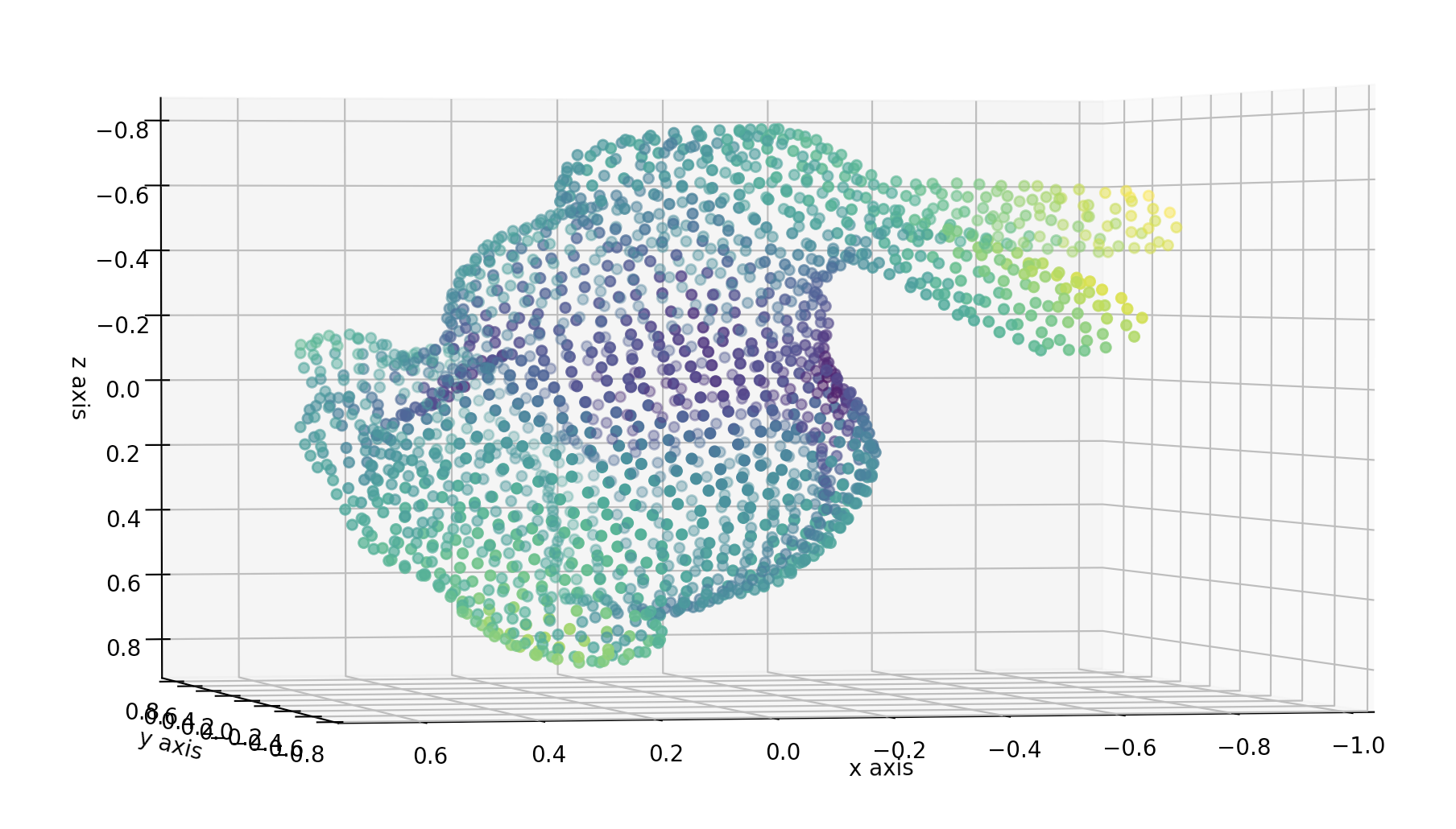
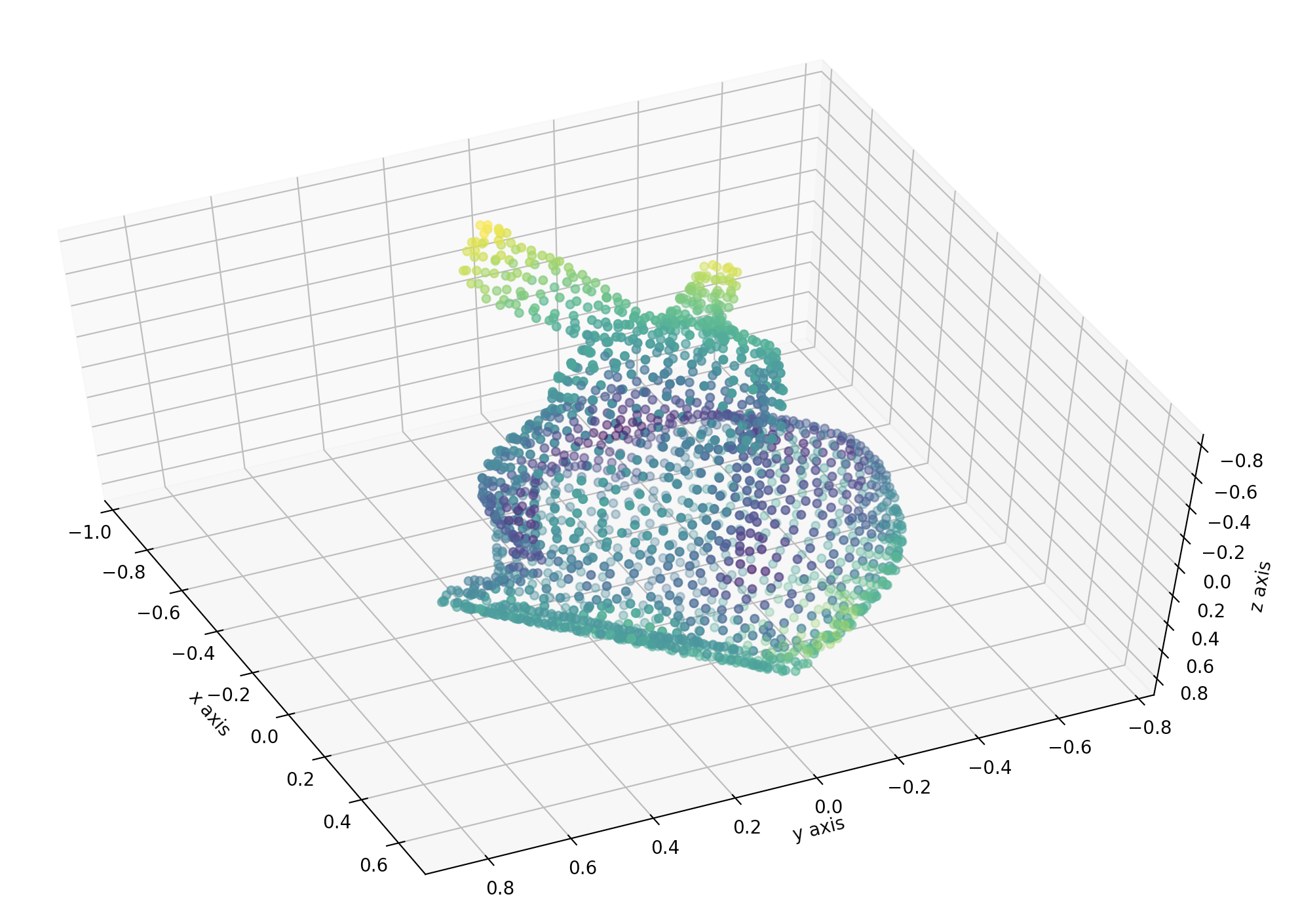
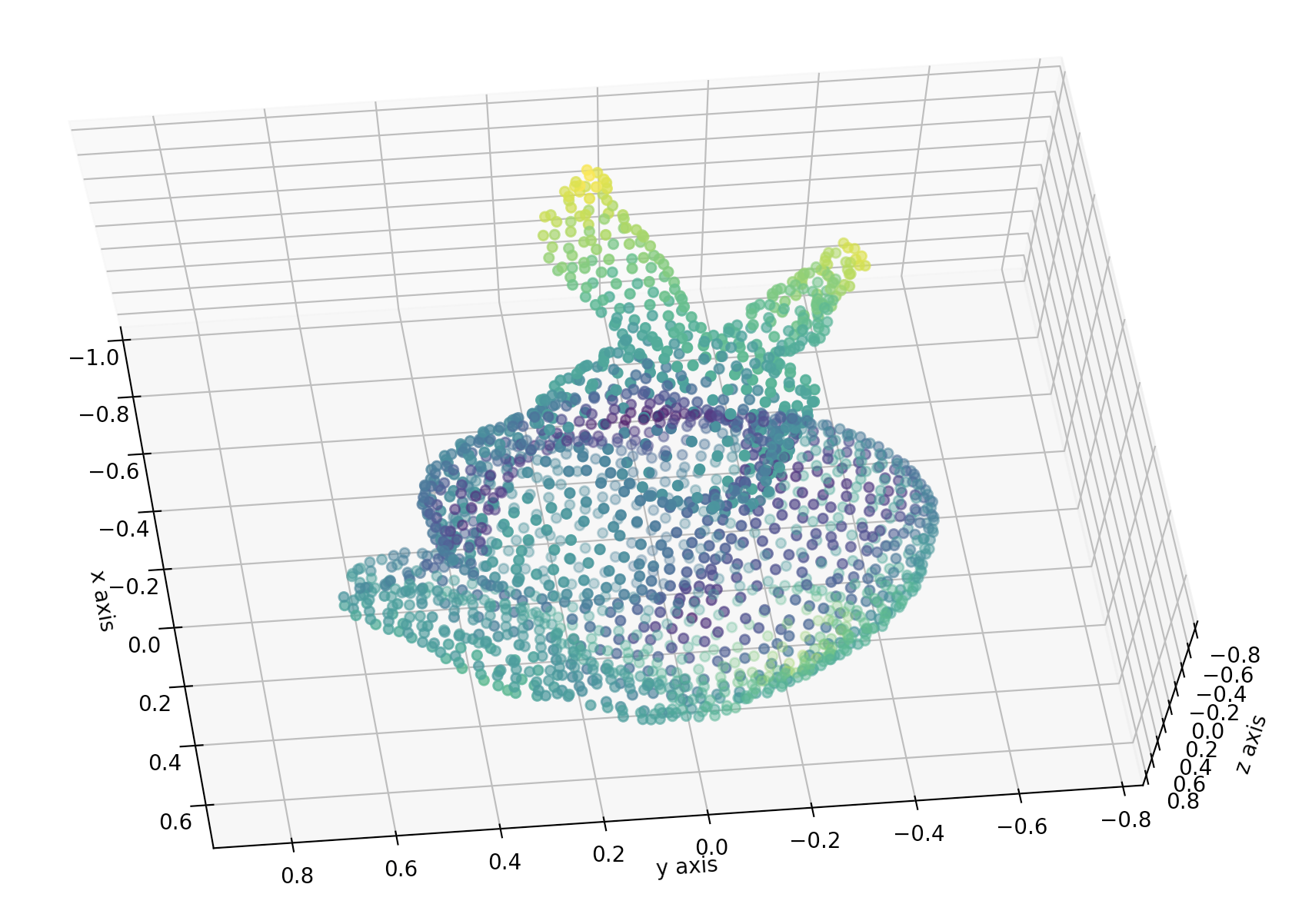
実際に実行してみるとうしろ脚のまわりの形もよく復元できていることがわかるので，ぜひご自分で確かめてみてください．

3次元復元できる条件

Tomasi-Kanade法は1990年代に開発された手法ということもあり，以下のかなり厳しい条件下でないと復元できないという欠点があります．

• 全ての視点から全てのランドマーク集合が観測されている
• 違う視点から観測されたランドマーク同士の関連付け(Data association)が済んでいる

しかし，この手法を知っておくと，幾何的制約を用いた他の3次元復元手法を理解する助けになるはずです．

手法

ではさっそく手法を見ていきましょう．

今回復元するのはコンピュータビジョン界の人気者であるこのうさぎさんです．

本当は2次元の点群画像のデータセットを用意したかったのですが，Tomasi-Kanade法の制約に合うようなものを見つけるのは難しいので，今回は3次元のうさぎさんをいろんな視点から撮影して，2次元の点群データセットを得ることにしました．
こうして得られたのが，最初にお見せした2次元の点群画像です．

Tomasi-Kanade法を用いると，2次元の点群画像のみから，3次元のうさぎさんを復元することができます．

問題設定

ある3次元の点群があったときに，コンピュータ上でそれをカメラで仮想的に撮影してみると，物体の像が得られます¹．

__この像と実際に撮影された点群の差がなるべく小さくなるように，3次元の点の位置とカメラの位置を定める__というのが，Tomasi-Kanade法の目的です．

3次元の点の座標とそれを撮影するカメラの座標の両方をうまく調整し，カメラに映った像が最初に撮影された像となるべく近くなるようにしようというわけです．
(ただしカメラ座標を取り出そうとすると記事が大きくなりすぎてしまうので，今回は3次元の点群を復元するのみとします)

言葉で説明してもいまいちピンと来ないかもしれないので，以降は数式を使って解説していきます．

モデル

ここまでは「点群」や「像」という単語を漠然と使ってきました．
しかし，言葉だけでははっきりと解説することが難しいので，ここからはこれらを数式で表していきます．

点群と像の関係

まず点群を表現します．
点群は3次元空間の点集合なので，点の数が$n$個だとすると，点群は$\mathbf{X}_{j} \in \mathbb{R}^{3},,j=1,\dots,n$と表されます．

次にカメラに映る像を表現します．
気をつけていただきたいのは，今回は視点が複数あることです．

$i$番目のカメラに映る点$\mathbf{X}_{j}$の像を$\mathbf{x}^{i}_{j}$と表すことにします．
すると，点群とその像の関係は次の図のようになります．

さて，Tomasi-Kanade法では，点$\mathbf{X}_{j}$と像$\mathbf{x}^{i}_{j}$の間に次の関係が成り立つことを仮定します．

$$
\hat{\mathbf{x}}^{i}_{j} = M^{i}\mathbf{X}_{j} + \mathbf{t}^{i}
$$

$\hat{\mathbf{x}}^{i}_{j}$は点群を平面に投影したときに得られる像です．
これはあくまでモデルによって得られた像なので，実際に撮影された像$\mathbf{x}^{i}_{j}$とは異なります．

$M^{i} \in \mathbb{R}^{2 \times 3}$は，点群と$i$番目のカメラに映るその像の関係を表しています．
$M$の具体的な中身が気になるところですが，いまのところは「$\mathbf{X}_{j}$が3次元で$\mathbf{x}^{i}_{j}$が2次元なので，その関係を行列で表しただけ」と思っていただければよいです．

$t^{i}$はオフセットです．
これは例えば$\mathbf{X}_{j} = [0, 0, 0]^{\top}$の点をカメラに投影しても，その像の位置はふつう$[0, 0]^{\top}$にはならなないので，その「ずれ」を表すためのものです．
ずれの大きさはカメラごとに異なるので$i$がついています．

問題設定

Tomasi-Kanade法の目的は，「コンピュータ上で点群を仮想的に撮影して得た像$\hat{\mathbf{x}}^{i}_{j}$と，実際に撮影された点群の像$\mathbf{x}^{i}_{j}$の差がなるべく小さくなるように，3次元の点の位置とカメラの位置を定める」というものです．

これを数式で表現すると，

$$
\sum_{i=1}^{m} \sum_{j=1}^{n} ||\mathbf{x}^{i}_{j}-\hat{\mathbf{x}}^{i}_{j}||^2
= \sum_{i=1}^{m} \sum_{j=1}^{n} ||\mathbf{x}^{i}_{j}-(M^{i}\mathbf{X}_{j} + \mathbf{t}^{i})||^2
$$

がなるべく小さくなるような $(M^{i}, \mathbf{X}_{j}, \mathbf{t}^{i})$ の組み合わせを見つける

ということに相当します．

解き方

ではさっそく解を見つけていきましょう．

とはいえ

$$
\sum_{i=1}^{m} \sum_{j=1}^{n} ||\mathbf{x}^{i}_{j}-\hat{\mathbf{x}}^{i}_{j}||^2
= \sum_{i=1}^{m} \sum_{j=1}^{n} ||\mathbf{x}^{i}_{j}-(M^{i}\mathbf{X}_{j} + \mathbf{t}^{i})||^2
$$

という式は未知定数が多すぎて解くのが非常に大変そうです．

Tomasi-Kanade法では，大きく分けて3段階の手順でこの問題をうまく解いていきます．

1. オフセット $\mathbf{t}^{i}$ を消去してしまう
2. $M^{i}$と$\mathbf{X}_{j}$の組み合わせの候補を特異値分解によって定める
3. 2で定めた解の候補の中から，光学的な制約を用いて$M^{i}$を定める．すると$\mathbf{X}_{j}$も勝手に定まる

オフセットの消去

$\mathbf{X}_{j}$，$M^{i}$，$\mathbf{t}^i$も全て不定だと解くのが大変ですが，このうち$\mathbf{t}^i$は最初に消去することができます．

誤差の式を$\mathbf{t}^i$で微分して$\mathbf{0}$とおくと，誤差を最小化する$\mathbf{t}^i$を閉じた形で表現できます．
これをもとの誤差の式に代入してしまえば，誤差の式から$\mathbf{t}^i$を消去することができます．

実際にやってみましょう．

誤差を最小化する $\mathbf{t}^{i}$ は次の式で求められます．

$$\frac{\partial}{\partial \mathbf{t}^{i}} \underset{kj}{\sum}
|| \mathbf{x}^{k}_{j} - (M^{k}\mathbf{X}_{j} + \mathbf{t}^{k}) ||^2
= \mathbf{0}$$

変形します．

$$\begin{aligned}
\begin{align}
\frac{\partial}{\partial \mathbf{t}^{i}} \underset{kj}{\sum}
|| \mathbf{x}^{k}_{j} - (M^{k}\mathbf{X}_{j} + \mathbf{t}^{k}) ||^2
&=
\frac{\partial}{\partial \mathbf{t}^{i}} \underset{kj}{\sum}
(\mathbf{x}^{k}_{j} - (M^{k}\mathbf{X}_{j} + \mathbf{t}^{k}))^{\top}
(\mathbf{x}^{k}_{j} - (M^{k}\mathbf{X}_{j} + \mathbf{t}^{k})) \\
&=
\frac{\partial}{\partial \mathbf{t}^{i}} \underset{kj}{\sum}
[
- 2(\mathbf{x}^{k}_{j})^{\top} \mathbf{t}^{k}
+ 2(M^{k}\mathbf{X}_{j})^{\top} \mathbf{t}^{k}
+ (\mathbf{t}^{k})^{\top} \mathbf{t}^{k}
] \\
&=
\frac{\partial}{\partial \mathbf{t}^{i}} \underset{j}{\sum}
[
- 2(\mathbf{x}^{i}_{j})^{\top} \mathbf{t}^{i}
+ 2(M^{i}\mathbf{X}_{j})^{\top} \mathbf{t}^{i}
+ (\mathbf{t}^{i})^{\top} \mathbf{t}^{i}
] \\
&=
\underset{j}{\sum}
[
- 2 \mathbf{x}^{i}_{j}
+ 2 M^{i}\mathbf{X}_{j}
+ 2 \mathbf{t}^{i}
] \\
&= \mathbf{0}
\end{align}
\end{aligned}$$

$$\begin{aligned}
\begin{align}
n\mathbf{t}^{i} &=
\underset{j}{\sum}
[
\mathbf{x}^{i}_{j} - M^{i}\mathbf{X}_{j}
] \\
\mathbf{t}^{i} &=
\frac{1}{n}
\underset{j}{\sum}
[
\mathbf{x}^{i}_{j} - M^{i}\mathbf{X}_{j}
] \\
\end{align}
\end{aligned}$$

ここで

$$\begin{aligned}
\begin{align}
\overline{\mathbf{x}^{i}} &:=
\frac{1}{n} \underset{j}{\sum} \mathbf{x}^{i}_{j} \\
\overline{\mathbf{X}} &:=
\frac{1}{n} \underset{j}{\sum} \mathbf{X}_{j}
\end{align}
\end{aligned}$$

とおくと， $\mathbf{t}^{i}$ は

$$\mathbf{t}^{i} =
\overline{\mathbf{x}^{i}} - M^{i}\overline{\mathbf{X}}$$

と表すことができます．
これをもとの誤差の式に代入すると

$$\underset{ij}{\sum}
|| \mathbf{x}^{i}_{j} - (M^{i}\mathbf{X}_{j} + \mathbf{t}^{i}) ||^2
=
\underset{ij}{\sum}
|| \mathbf{x}^{i}_{j}

• (M^{i}\mathbf{X}_{j}

• \overline{\mathbf{x}^{i}}

• M^{i}\overline{\mathbf{X}}) ||^2$$

となり，$\mathbf{t}^{i}$ を消去することができました．

$\mathbf{t}^{i}$を消せたのはよいのですがまだ少し煩雑です．
ここで$\mathbf{X}_{j}$に着目してみましょう．現時点では$\mathbf{X}_{j}$になんの制約も与えられていません．
すなわち$\mathbf{X}_{j}$は任意の値をとることが可能ですから，$\mathbf{X}_{j}$の平均値$\overline{\mathbf{X}}$も任意の値に設定することができます．

計算を簡単にするため，

$$\overline{\mathbf{X}} := \mathbf{0}$$

と定めると，

$$\begin{aligned}
\begin{align}
\underset{ij}{\sum}
|| \mathbf{x}^{i}_{j} - \hat{\mathbf{x}}^{i}_{j} ||^2
&=
\underset{ij}{\sum}
|| \mathbf{x}^{i}_{j}

• (M^{i}\mathbf{X}_{j}

• \overline{\mathbf{x}^{i}}) ||^2 \\
  &=
  \underset{ij}{\sum}
  || \mathbf{x}^{i}_{j}

• \overline{\mathbf{x}^{i}}
• M^{i}\mathbf{X}_{j} ||^2.
  \end{align}
  \end{aligned}$$

さらに $\mathbf{x}^{i}_{j}$ を

$$\mathbf{x}^{i}_{j} \leftarrow
\mathbf{x}^{i}_{j} - \overline{\mathbf{x}^{i}}$$

というふうに上書きすると，誤差の式は

$$\underset{ij}{\sum}
|| \mathbf{x}^{i}_{j} - (M^{i}\mathbf{X}_{j} + \mathbf{t}^{i}) ||^2
=
\underset{ij}{\sum}
|| \mathbf{x}^{i}_{j} - M^{i}\mathbf{X}_{j} ||^2$$

というかたちにまで簡略化することができます．

さて，不定な変数が$\mathbf{X}_{j}$と$M^{i}$のみになりました．
愚直に探索して解を求めてもよいのですが，$\mathbf{X}_{j}$と$M^{i}$の両方が不定なので，これでもまだ解くのが大変です．
そこで，特異値分解を利用して一気に解の候補を出してしまおうというのがTomasi-Kanade法の戦略です．

SVDによる3次元座標の計算

Tomasi-Kanade法では観測値行列(measurement matrix)という行列をつくり，これを特異値分解(SVD)することで$\mathbf{X}_{j}$と$M^{i}$の候補を定めます．
観測値行列といっても簡単で，単にカメラによって得られた(観測された)2次元の座標を並べて行列にしたものです．

$$\begin{aligned}
W =
\begin{bmatrix}
\mathbf{x}^{1}_{1} & \dots & \mathbf{x}^{1}_{j} & \dots & \mathbf{x}^{1}_{n} \\
\vdots & \ddots & & & \vdots \\
\mathbf{x}^{i}_{1} & & \mathbf{x}^{i}_{j} & & \mathbf{x}^{i}_{n} \\
\vdots & & & \ddots & \vdots \\
\mathbf{x}^{m}_{1} & \dots & \mathbf{x}^{m}_{j} & \dots & \mathbf{x}^{m}_{n} \\
\end{bmatrix}
\end{aligned}$$

それぞれの$\mathbf{x}^{i}_{j}$は2次元なので，$W$は$2m \times 3$の行列です．

推定値$\hat{\mathbf{x}}^{i}_{j}$も同様に並べて行列にしてみましょう．

$$
\begin{aligned}
\hat{W} =
\begin{bmatrix}
\hat{\mathbf{x}}^{1}_{1} & \dots & \hat{\mathbf{x}}^{1}_{j} & \dots & \hat{\mathbf{x}}^{1}_{n} \\
\vdots & \ddots & & & \vdots \\
\hat{\mathbf{x}}^{i}_{1} & & \hat{\mathbf{x}}^{i}_{j} & & \hat{\mathbf{x}}^{i}_{n} \\
\vdots & & & \ddots & \vdots \\
\hat{\mathbf{x}}^{m}_{1} & \dots & \hat{\mathbf{x}}^{m}_{j} & \dots & \hat{\mathbf{x}}^{m}_{n} \\
\end{bmatrix}
\end{aligned}
$$

すると$\hat{\mathbf{x}}^{i}_{j} = M^{i}\mathbf{X}_{j}$より，$\hat{W}$は

$$
\begin{aligned}
\hat{W}
=
M\mathbf{X}
=
\begin{bmatrix}
M^{1} \\
\vdots \\
M^{i} \\
\vdots \\
M^{m}
\end{bmatrix}
\begin{bmatrix}
\mathbf{X}^{1} &
\dots &
\mathbf{X}^{j} &
\dots &
\mathbf{X}^{n}
\end{bmatrix}
\end{aligned}
$$

と表すことができます．

ここで注目していただきたいのは，$\hat{W}$のランクです．
$M^{i}$は$2 \times 3$の行列であり，$\mathbf{X}_{j}$は3次元のベクトルですから，$\hat{W}$のランクはせいぜい3です．

では$W$はどうでしょうか．
$\mathbf{x}^{i}_{j}$は最初に定義したモデル$\hat{\mathbf{x}}^{i}_{j} = M^{i}\mathbf{X}_{j}$にぴったり従うわけではありません．
たとえばノイズ$\mathbf{\epsilon}$が乗っていることもあるでしょう．

$$
\mathbf{x}^{i}_{j} = M^{i}\mathbf{X}_{j} + \mathbf{\epsilon}
$$

よって，$W$のランクが3以下になることはまずありません．
しかし，$\mathbf{x}^{i}_{j}$がモデルによく従っているなら，ランク3の行列で観測値行列$W$を近似することはできます．
これがTomasi-Kanade法のキモに相当する部分で，以降の章で大事になってきます．

特異値分解による解の候補の計算

繰り返しになりますが，Tomasi-Kanade法の戦略は，観測値行列$W$を特異値分解して一気に$M$と$\mathbf{X}$の候補を求めてしまおうというものです．
ただし$M$と$\mathbf{X}$は，先ほどお見せしたように

$$
\begin{aligned}
M
&=
\begin{bmatrix}
M^{1} \\
\vdots \\
M^{i} \\
\vdots \\
M^{m}
\end{bmatrix} \\
\mathbf{X}
&=
\begin{bmatrix}
\mathbf{X}^{1} &
\dots &
\mathbf{X}^{j} &
\dots &
\mathbf{X}^{n}
\end{bmatrix}
\end{aligned}
$$

という行列です．

$W$を特異値分解してみましょう．

$W$ は $2m \times n$ の行列なので，

$$
\begin{aligned}
\begin{align}
U &\in \mathbb{R}^{2m \times 2m} \\
D &\in \mathbb{R}^{2m \times n} \\
V^{\top} &\in \mathbb{R}^{n \times n}
\end{align}
\end{aligned}
$$

という3つの行列に分解することができます．

さて，もしこの$W$を構成する全ての$\mathbf{x}^{i}_{j}$がモデル$\hat{\mathbf{x}}^{i}_{j} = M^{i}\mathbf{X}_{j}$にぴったり従う(すなわち$\mathbf{x}^{i}_{j} = M^{i}\mathbf{X}_{j}$となる)のであれば，行列$W$のランクは3以下になります．
これはすなわち，行列$D$の対角成分のうち，3つめまでに全てのエネルギーが集中するということを意味します．

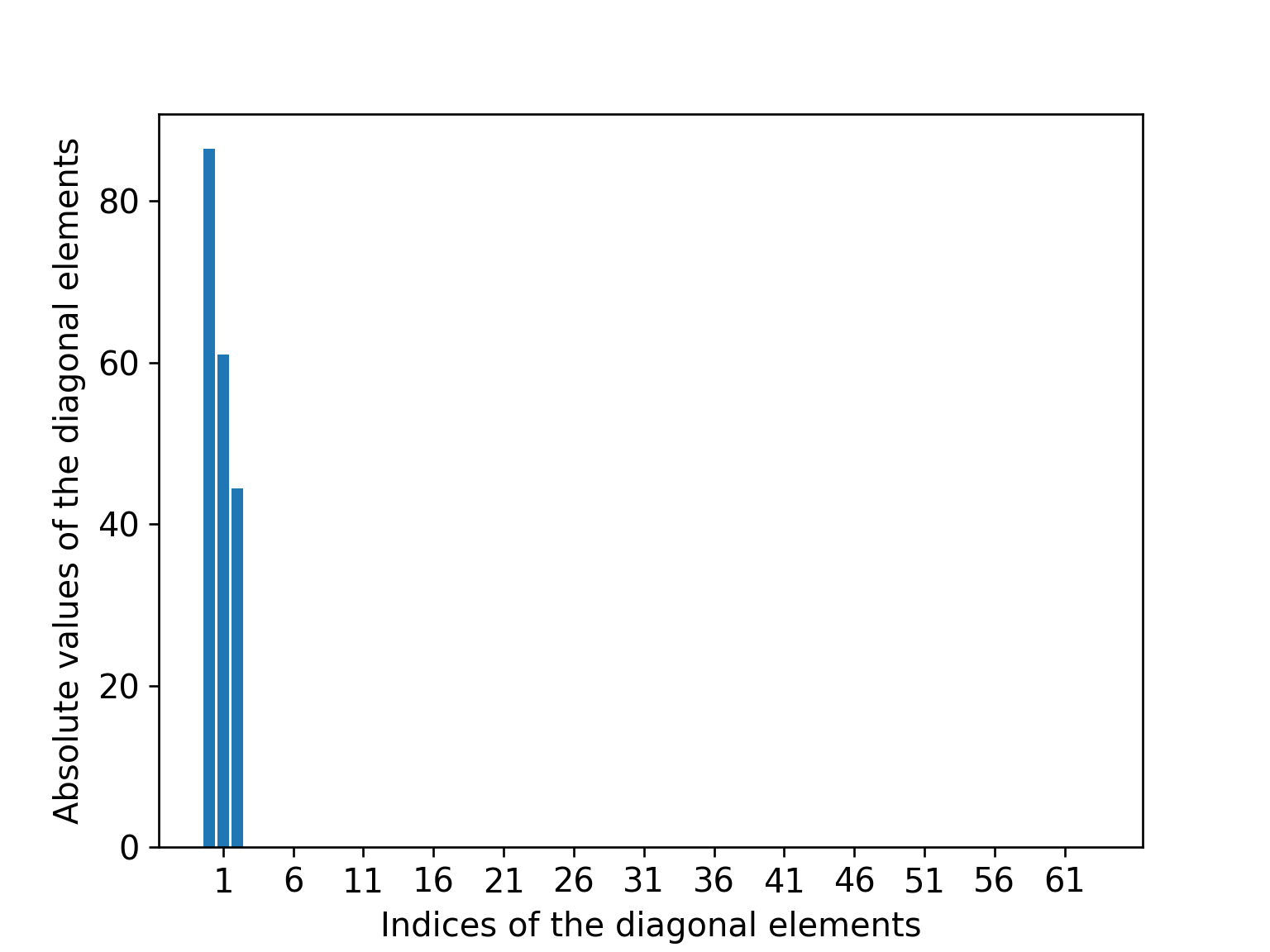    行列$D$の対角成分の絶対値 (観測された点群にノイズが乗っていない場合)

実際にはノイズが乗ったりする²ので，$\mathbf{x}^{i}_{j}$はぴったりモデルに従うわけではありません．
しかし，$\mathbf{x}^{i}_{j}$がモデルに"よく"従っている(すなわち$\mathbf{x}^{i}_{j} \approx M^{i}\mathbf{X}_{j}$となる)のであれば，$D$の対角成分のうち左上から数えて4つ目以降は，3つ目までと比べるとかなり小さい値になります．

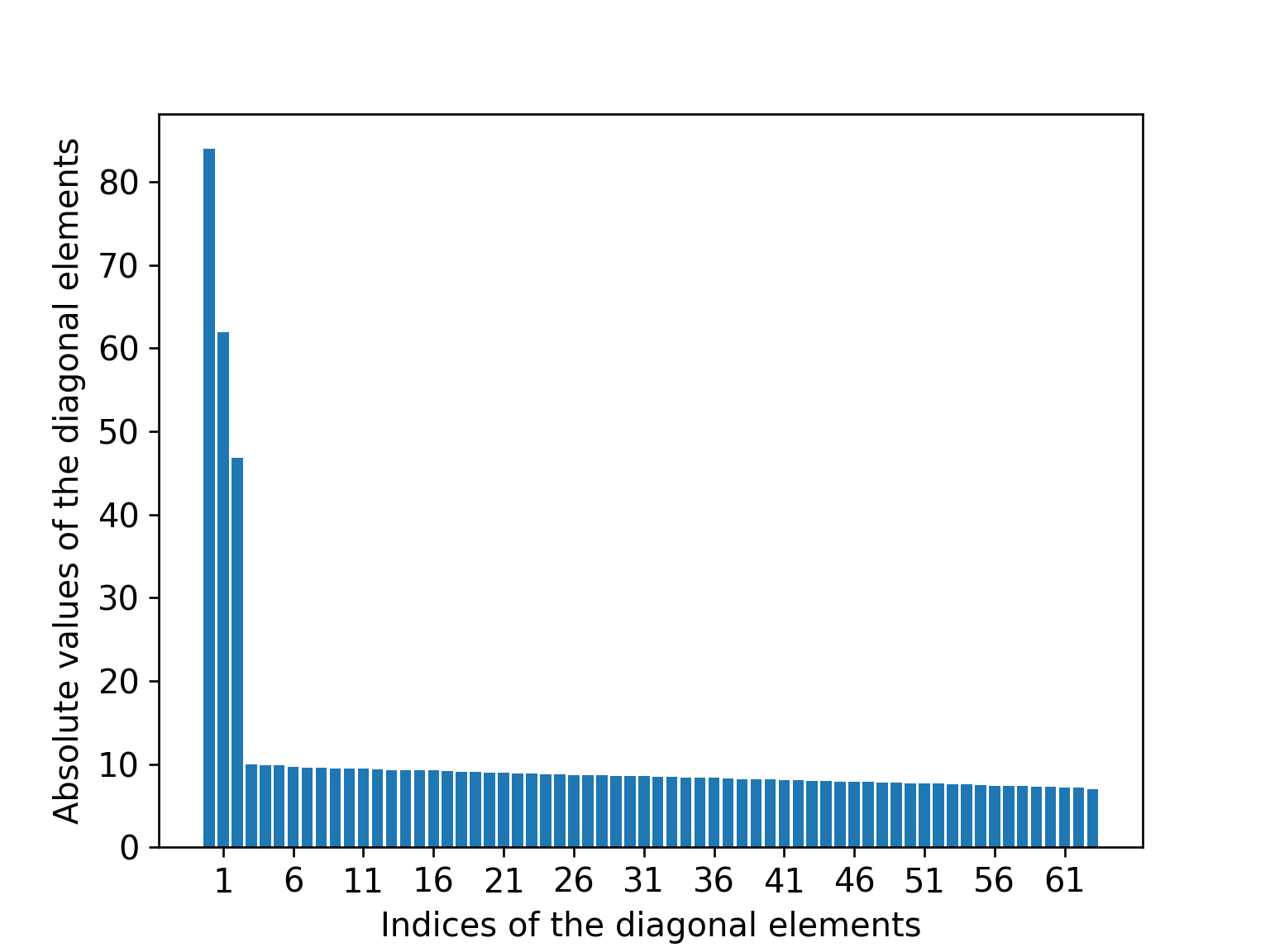    行列$D$の対角成分の絶対値 (観測された点群にノイズが乗っている場合)

よって，$D$の対角成分の4つ目以降と，関連する$U$と$V^{\top}$の要素を削除してから観測値行列を再構成しても，その行列は $W$ とほぼ変わらないものになるはずです．

$$\begin{aligned}
\begin{align}
U_{2m \times 3} &\in \mathbb{R}^{2m \times 3} \\
D_{3 \times 3} &\in \mathbb{R}^{3 \times 3} \\
V^{\top}_{3 \times n} &\in \mathbb{R}^{3 \times n}
\end{align}
\end{aligned}$$

$$
W \approx U_{2m \times 3} D_{3 \times 3} V^{\top}_{3 \times n}
$$

これが先ほど出てきた「ランク3の行列で$W$を近似できる」ということの意味です．

$\hat{W} = M\mathbf{X}$より，$U_{2m \times 3}$，$D_{3 \times 3}$，$V^{\top}_{3 \times n}$という3つの行列をうまくかけ合わせれば，観測値行列$W$をよく近似する$M$と$\mathbf{X}$の組み合わせを作ることができるはずです．

3つの行列をどう組み合わせればよいか

$U_{2m \times 3}$，$D_{3 \times 3}$，$V^{\top}_{3 \times n}$という3つの行列をかけ合わせれば$M$と$\mathbf{X}$を求められることはわかったのですが，ではどのようにかけ合わせればよいのでしょうか．

例えば，ぱっと思いつくだけでも

(A)

$$\begin{aligned}
\begin{align}
\hat{M} &= U D \\
\hat{\mathbf{X}} &= V^{\top}
\end{align}
\end{aligned}$$

(B)

$$\begin{aligned}
\begin{align}
\hat{M} &= U \\
\hat{\mathbf{X}} &= D V^{\top}
\end{align}
\end{aligned}$$

(C)
$$\begin{aligned}
\begin{align}
\hat{M} &= U D^{1/2} \\
\hat{\mathbf{X}} &= D^{1/2} V^{\top}
\end{align}
\end{aligned}$$

という組み合わせが思いつきますし，当然(A)，(B)，(C)のいずれも$\hat{M}\hat{\mathbf{X}} = \hat{W} \approx W$を満たすことができます．

さらには任意のアフィン行列 $Q \in \mathbb{R}^{3 \times 3}$ を使って　

(D)

$$\begin{aligned}
\begin{align}
\hat{M} &= U D Q \\
\hat{\mathbf{X}} &= Q^{-1} V^{\top}
\end{align}
\end{aligned}$$

としても $\hat{W} = \hat{M}\hat{\mathbf{X}}$ が成り立ってしてしまいます．

さて，どの組み合わせが正しいのでしょうか？

行列の組み合わせを定める方法

なんの制約もないと$M$も$\mathbf{X}$も定めることができません．

先ほど示した(A)(B)(C)(D)いずれのパターンも(D)のパターンのみで表せるため，ここは(D)のパターンを選択し，$M$と$\mathbf{X}$を定める問題を，未知の行列$Q$を定める問題に置き換えてやるのがよさそうです．

もちろんなんの制約もないと$Q$を定めることができないので，何らかの制約を入れてやる必要があります．

制約

Tomasi-Kanade法では次のような制約を用います．

    $\hat{M}$を構成する部分行列$\hat{M}^{i}$を

$$
\hat{M}^{i} = \begin{bmatrix}
{\hat{\mathbf{m}}^{i}_{1}}^{\top}\\
{\hat{\mathbf{m}}^{i}_{2}}^{\top}
\end{bmatrix}
$$

    と表すとき，$\mathbf{m}^{\top}_{1}$と$\mathbf{m}^{\top}_{2}$は直交し，

$$
\begin{align}
\hat{\mathbf{m}}^{\top}_{1} \hat{\mathbf{m}}_{1} &= 0 \\
\hat{\mathbf{m}}^{\top}_{2} \hat{\mathbf{m}}_{2} &= 0 \\
\hat{\mathbf{m}}^{\top}_{1} \hat{\mathbf{m}}_{2} &= \hat{\mathbf{m}}^{\top}_{2} \hat{\mathbf{m}}_{1} = 1
\end{align}
$$

    を満たす．

制約の意味を解説しようとすると投影モデルについて説明しなければならなくなってしまうので，これはfootnote³に譲ることにして，「とりあえずこの制約を入れるとうまく解が定まる」という程度に認識していただければと思います．

では，制約を満たすように$\hat{M}^{i}$を定めていきます．

制約を書き換えると$\hat{M}^{i}{\hat{M}^{i}}^{\top} = I$となりますが，$\hat{M}^{i}$は視点と同じ数だけあるので，全ての$\hat{M}^{i}$に対してこの制約を完全に満たすことができるわけではありません．

そこで誤差関数

$$
\begin{align}
E(Q)
&=
\sum_{i=1}^{m} || \hat{M}^{i}{\hat{M}^{i}}^{\top} - I ||^{2}_{F} \\
&=
\sum_{i=1}^{m} || UDQ (UDQ)^{\top} - I ||^{2}_{F}
\end{align}
$$

を定め，これを最小化するような$Q$を求めます．

もちろん自分で勾配を導出して$E(Q)$を最小化する$Q$を求めてもよいのですが，Chainerを使えば勾配の導出も最小化も全てやってくれるので，今回の実装では全て任せてしまっています．

$E(Q)$を最小化する$Q$が求まれば，あとはこれを(D)に代入して，最適な$M$と$\mathbf{X}$を定めることができます．

おわりに

以上がTomasi-Kanade法の解説です．疑問に思った点やおかしいと思った部分があればぜひコメント等でお伝えください．

参考文献

[1] Tomasi Carlo and Takeo Kanade. "Shape and motion from image streams under orthography: a factorization method." International Journal of Computer Vision 9.2 (1992): 137-154.
[2] Hartley, Richard, and Andrew Zisserman. Multiple view geometry in computer vision. Cambridge university press, 2003.

1. 通常は物体と像の関係としてピンホールカメラモデルを仮定することが多いのですが，Tomasi-Kanade法では正投影モデルを仮定しています． ↩

2. ノイズの原因としては，たとえば画像から特徴点を抽出したときにdata associationにミスがあったり，Tomasi-Kanade法内部で使っているカメラモデルが実際のカメラとは異なっていたりするといったものが挙げられるでしょう． ↩

3. $M^{i}$はカメラの内部パラメータ$K \in \mathbb{R}^{2 \times 3}$と姿勢を表現する行列$R^{i} \in \mathrm{SO}(3)$を用いて$M^{i} = R^{i}K$と表されます．この$K$の中身によって制約が変わってきます．今回は正投影モデルを採用しているので$K^{i} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix}$です. ↩