記事概要
競技プログラミングの鉄則 演習問題のA15のとりあえず動くコードと説明.
https://atcoder.jp/contests/tessoku-book/tasks/tessoku_book_o
注意
アルゴリズム初心者が書いています.時間内の動作は確認してますが、必ずしも最適解ではないです.
とりあえずコード
/////////////////////
// A15-Compression //
/////////////////////
#include <iostream>
#include <vector>
#include <algorithm>
using std::vector;
int main(void)
{
//============================== 入力 ==============================//
int N;
std::cin >> N;
vector<int> A(N + 1);
for (int i = 1; i <= N; ++i) {
std::cin >> A[i];
}
//============================== 計算 ==============================//
// Aをソートした配列A_sortedを作成
vector<int> A_sorted = A;
std::sort(A_sorted.begin(), A_sorted.end());
/*
std::cout << "ソート後 -> ";
for (int i = 0; i <= N; ++i) {
std::cout << A_sorted[i] << " ";
}
std::cout << std::endl;
*/
// std::cout << "配列Aのソート 完了\n";
// A_sortedを条件により圧縮したA配列_sorted_compressionを作成
vector<int> A_sorted_compression = A_sorted;
int idx = 2;
A_sorted_compression[1] = 1;
while (idx <= N) {
int to_compression_val = A_sorted_compression[idx - 1] + 1;
// A_sorted_compression[i]の値と同じ値を持つ範囲を調べる.
int left = idx, right = idx;
while (right + 1 <= N && A_sorted_compression[right + 1] == A_sorted_compression[left]) {
right += 1;
}
// std::cout << "l, r " << left << " " << right << "\n";
for (int i = left; i <= right; ++i) {
A_sorted_compression[i] = to_compression_val;
}
idx = right + 1;
}
/*
std::cout << "圧縮後 -> ";
for (int i = 0; i <= N; ++i) {
std::cout << A_sorted_compression[i] << " ";
}
std::cout << std::endl;
*/
// std::cout << "A_sortedの圧縮 完了\n";
// A[i] -> B[i]となる対応表を作成
vector<int> compressionTable((int)A_sorted_compression.back() + 1);
for (int i = 1; i <= N; ++i) {
compressionTable[A_sorted_compression[i]] = A_sorted[i];
}
/*
for (int i = 1; i < (int)compressionTable.size(); ++i) {
std::cout << compressionTable[i] << " ";
}
std::cout << std::endl;
*/
// std::cout << "対応表の作成 完了\n";
// Bを作成
vector<int> B(N + 1);
for (int i = 1; i <= N; ++i) {
B[i] = std::lower_bound(compressionTable.begin(), compressionTable.end(), A[i]) - compressionTable.begin();
}
// std::cout << "Bの作成 完了\n";
//============================== 出力 ==============================//
for (int i = 1; i <= N; ++i) {
std::cout << B[i] << " ";
}
std::cout << std::endl;
}
コード説明
この問題は、与えられた配列Aのある要素A[i]が配列Aの中で何番目に小さいかを対応する位置に格納した配列Bを作成することが目的です.
上のコードは、以下の4手順で配列Aを圧縮しています.
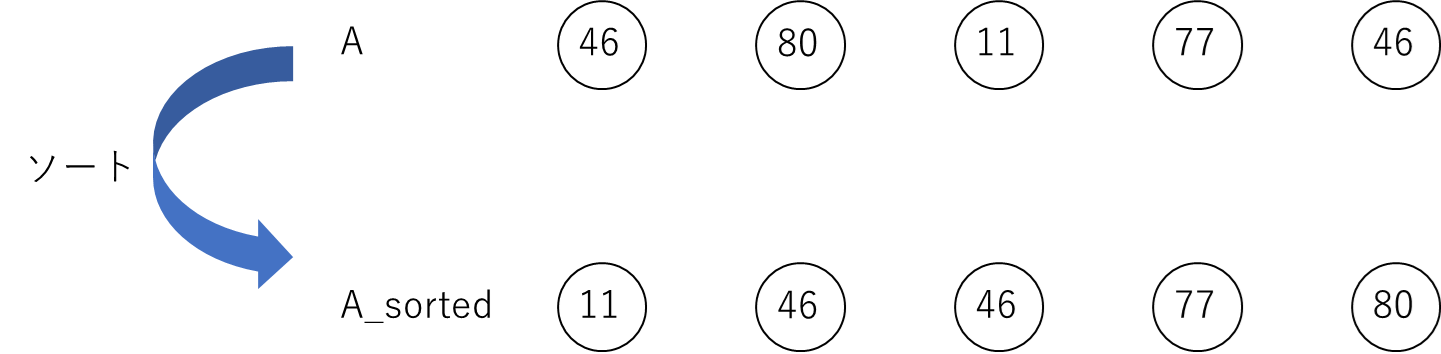
① Aをソートした配列A_sortedを作成
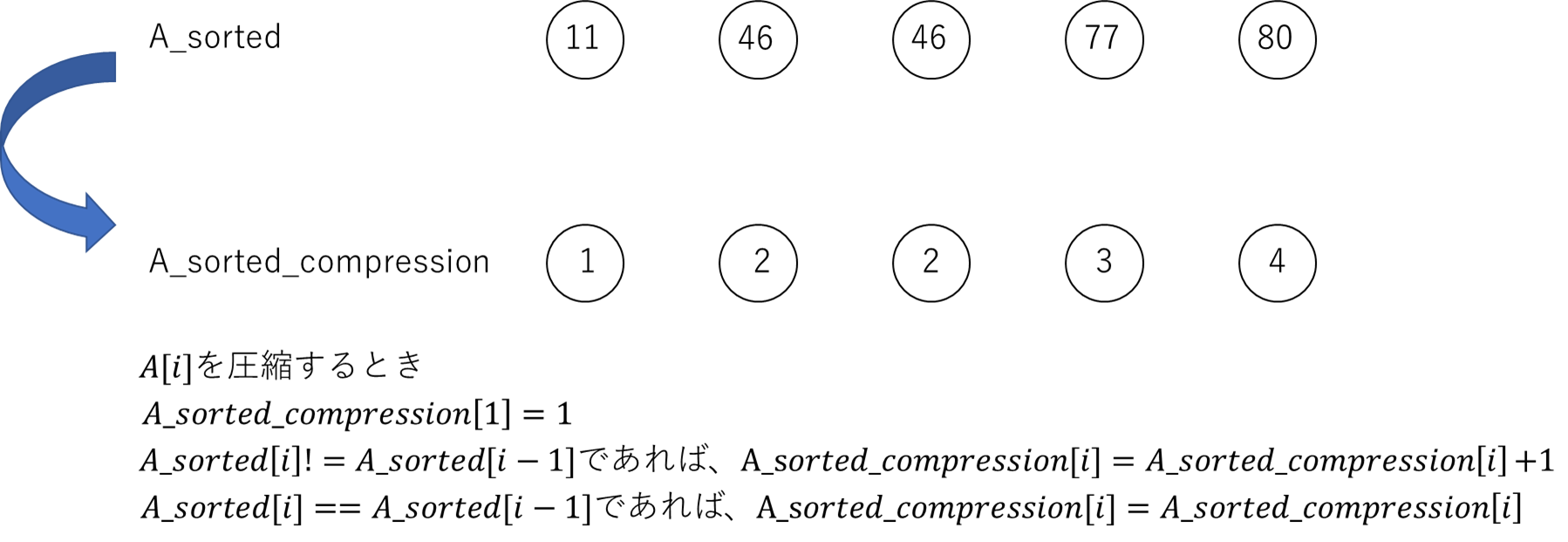
② A_sortedに対し、小さい値から順番に1,2,3…と置き換えた配列A_sorted_compressionを作成
③ 全ての要素に対し、compressionTable[A_sorted_compression[i]] = A_sorted[i]が成り立つcompressionTableを作成
④ compressionTableを元に、配列Aを圧縮した配列Bを作成
下でそれぞれについて説明します.
① A_sortedを作成
先に説明したように、この問題では配列Aのある要素がA内で何番目に小さいかを求める必要があるため、ひとまずソートを行います.
② A_sorted_compressionを作成
③ compressionTable作成
①と②で作成した配列を元に、compressionTable[A_sorted_compression[i]] = A_sorted[i]が成り立つような配列を作成します.
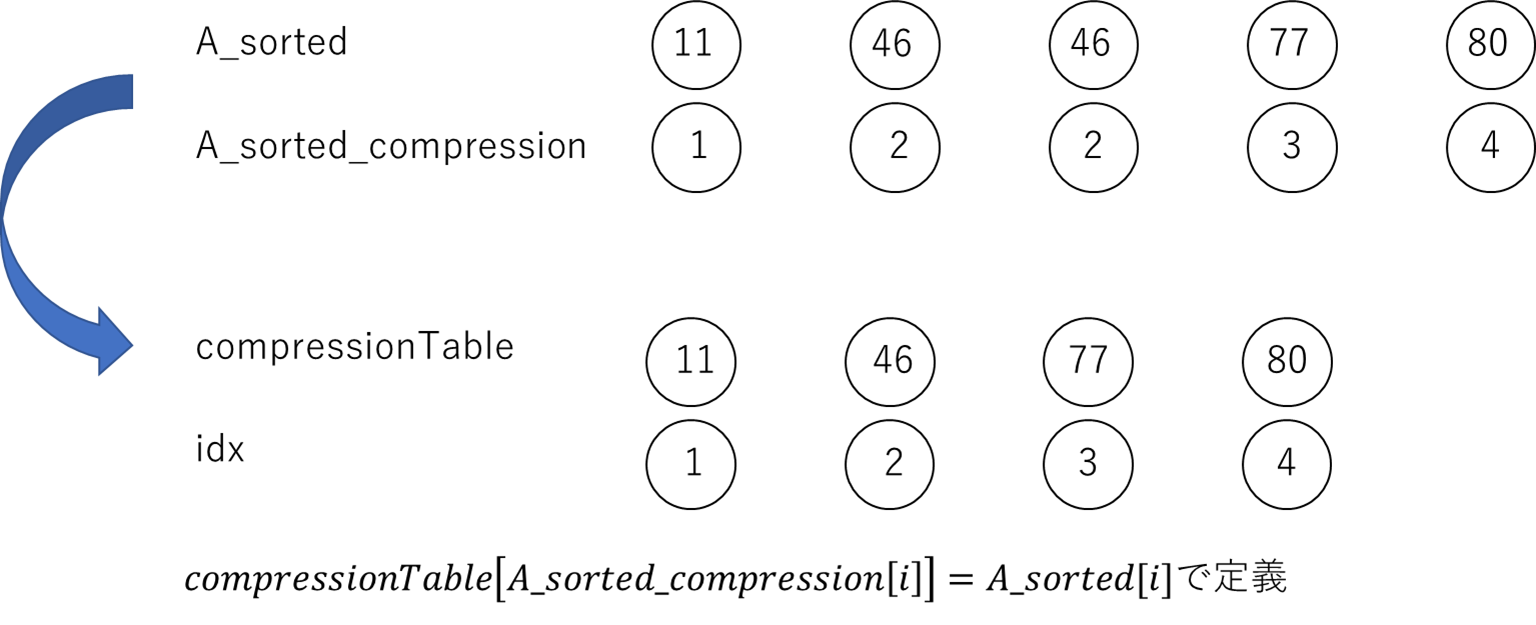
Aを圧縮した配列Bを作成
compressionTableはAとBの対応表で、compressionTalbe[B[i]] = A[i]が成り立ちます.A[i]の各要素をcompressionTableから二分探索で探索し、その格納位置の添え字をB[i]に格納します.これにより、求める配列Bができました.

終わりに
この手法は「座標圧縮」(多分)っていうらしいですね.