はじめに
この記事は、慶應理工アドベントカレンダーの16日目の記事です。他の方の記事(ainnoooさんのXDPの記事、武田のぶひこ(kanade)さんのディストロ記事、sanguisorbaさんのアセンブラ記事、他にもいっぱい)が面白いし凄いのでぜひ!
また、昨日の記事はBBでのスキャンマッチングです。ぜひこの記事も読んでくださいね〜
ジューコフスキー翼とは?
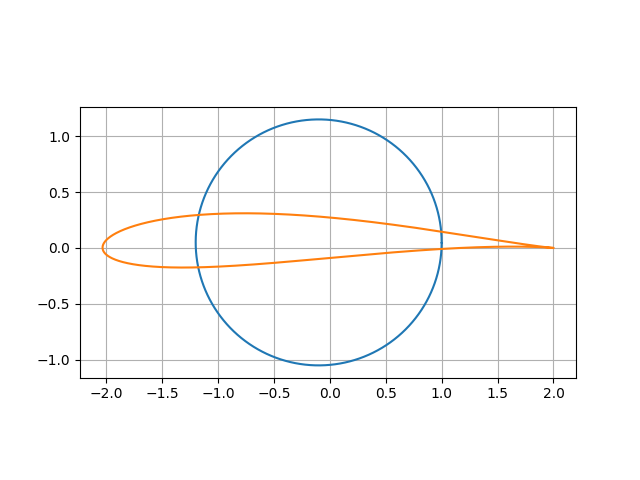
簡単に言えば、航空機の翼の形状について理論的に求めたものです。実際の航空機の翼をスパッと切った断面図(翼型と言います)に近い翼型が得られます。円柱周りの完全流体(粘性が無い流体)の流れが解明されていることを利用して等角写像による変換を行い、円柱の断面図から翼型を求めるというものです。非常にシンプルな式で得られる、基本的な翼型です。(下の図で青色の円を写像したものが、オレンジの翼型でジューコフスキー翼と呼びます。)
円柱周りの完全流体の流れについて
まず、速度$V$、圧力$P_∞$、密度$ρ$で一様に流れている完全流体中に、流れに直角に置かれた円柱を考えます。長さは無限に長いものとします。このような二次元流を考える時円中表面に沿った速度$v$は、その点と流れに対する角を$\theta$と置いたときに
v = 2V\sin(\theta)
で表され、さらにベルヌーイの式から円柱表面の圧力$p$は、
p = p_∞ + \frac{1}{2} \rho V^2 (1-4\sin^2(\theta))
と求められます。
そして圧力$p$を円柱で周回積分し、抗力$F$を求めると、
F = - \oint p(\theta)\cos(\theta) d\theta = 0
となり、抗力が生じないという結果になります。これは直感と反しています(d'Alembertのパラドックス)が、粘性が無いと仮定したためです。現実の流体では粘性は当然あるため、このような結果にはなりません。
一様な流れの完全流体の中に置かれた円柱には、揚力も抗力も働かないことが分かりましたが、圧力分布について違うケースを考えてみます。
先程までの一様な流れに加え、円柱の周りを循環するような流れが加わった状態を考えます。
ここで循環とは、閉曲面を短い線分に分割した場合について、それぞれの線分の長さと速度の線分方向の成分$V_t$を掛け合わせたものを一周した総和のことです。一般に循環は$\Gamma$という記号であらわし、下記の積分で計算することが可能です。
\Gamma = \oint v_t ds = \oint v \cos(θ)ds
ここで円柱の半径を$a$、循環の強さを$\Gamma$とすると、循環流による円柱表面の流速$V$は、
v = \frac{\Gamma}{2\pi a}
で与えられ、重ね合わせの原理により、この状態における表面の流速は、
v = 2V\sin(\theta) + \frac{\Gamma}{2\pi a}
となります。
さらに、ベルヌーイの式より円柱表面の圧力$p$は、
p = p_∞ + \frac{1}{2} \rho V^2 - \frac{1}{2} \rho V^2 (2\sin(\theta) + \frac{\Gamma}{2\pi a V})^2
となり、以下の積分に$p$を代入し積分すると、一様な流れに直角な力$F$(揚力)が求められます。
F = -a \oint p \sin(\theta)d\theta = \rho V \Gamma
この式はクッタ・ジューコフスキーの定理と呼ばれており、循環値と揚力の関係性を示します。また飛行機の翼についても、翼の周りの空気が循環していることによって生み出される揚力をこの式で説明することが出来ます。
ジューコフスキー変換
そもそもジューコフスキー変換とは
等角写像(関数行列が回転行列のスカラ倍)による変換で円柱を翼型に変換できれば、当然翼型周りの流れも、円柱周りの流れと同じように考えることができます。(等角写像による変換ということは、変換後図形の微小部分が元の図形(円柱)と相似になっているということです。微小部分が相似のため、同様の流れとできます。)つまり、完全流体中の揚力について計算し求めたクッタ・ジューコフスキーの定理が、変換後の図形にも適用できるということです。
そしてもっともシンプルな等角写像関数が、今回取り扱うジューコフスキー変換であり、ジューコフスキー変換によって得られる翼型をジューコフスキー翼と呼びます。また、ジューコフスキー翼を改良したものとして、カルマンートレフツ翼やフォン・ミーゼス翼などが存在します。
ジューコフスキー変換の計算
まず最初に、実軸が$x$であり、虚軸が$y$であるとした複素数平面を考えます。ここで虚数単位$i$を用いて、この座標中の点は$x+iy$と表すことが出来ます。また、この平面を$z$平面と呼びます。
また、実軸が$\xi$、虚軸が$\eta$であるとした複素数平面も同様に、座標中の点を$\xi +i\eta$で表すことができ、この平面を$\zeta$平面と呼びます。
そして、以下の式によって、$z$平面上の点を$\zeta$平面上に写像する変換を、ジューコフスキー変換と呼びます。$a$は実定数のパラメタです。
\zeta = z + \frac{a^2}{z}
これだけです。C++の場合、complex.hをインクルードしてやれば複素数計算も一瞬なので、この写像の式をそのまま書くだけです。
C++での実装
ソースコードは下記の通りです。グラフ描写には↓のプロジェクトの、matplotlib-cppを用いました。
https://github.com/lava/matplotlib-cpp
コンパイルに関しては
https://hirlab.net/nblog/category/programming/art_826/
の記事を参考にしました。matplotlibcpp.hをインクルードするだけです。(matplotlib、python自体のインストールを忘れずに!)
# include <iostream>
# include <math.h>
# include <bits/stdc++.h>
# include "matplotlibcpp.h"
namespace plt = matplotlibcpp;
using namespace std;
int main() {
//円の座標プロットをどのくらい細かく区切るかを決めます。
int plots = 1080;
//実定数パラメタa、写像前の円の半径radius、中心center_xとcenter_yを代入します。
double a_value = 1;
double radius = 1.1;
double center_x = -0.1;
double center_y = 0.05;
//z_arrayとzeta_arrayは複素数complexのvector、x_arrayとy_arrayとxi_arrayとeta_arrayはvectorで全ての長さはplotsです。
vector<complex<double>> z_array(plots);
vector<double> x_array(plots),y_array(plots);
vector<complex<double>> zeta_array(plots);
vector<double> xi_array(plots),eta_array(plots);
for (double i = 0; i < plots; ++i){
//実軸をx、虚軸をyとした半径が変数radiusの円座標を生成します。
z_array[i] = complex<double>(radius*cos(i/plots*2*M_PI) + center_x,radius*sin(i/plots*2*M_PI) + center_y);
x_array[i] = real(z_array[i]);
y_array[i] = imag(z_array[i]);
//zeta_arrayにはジューコフスキー変換の式で写像された座標が入ります。
zeta_array[i] = complex<double>(z_array[i] + (a_value*a_value)/z_array[i]);
xi_array[i] = real(zeta_array[i]);
eta_array[i] = imag(zeta_array[i]);
}
plt::grid(true);
//グラフのアスペクト比を1に設定します。
plt::set_aspect(1);
plt::plot(x_array,y_array);
plt::plot(xi_array,eta_array);
plt::show();
return 0;
}
以上のとても簡単なスクリプトは、式をそのままC++で書いてやっただけです。(これは別談なのですが、昔のC++教科書曰く、complexを含む計算の時は自動でintをcomplexに変換してくれたらしいです。昔のほうが便利だった気がします。)
翼の形状とパラメータの関係
次に、パラメタ(実定数$a$、写像前の円の半径$r$、中心座標$x$、$y$)と、翼の形状の関係性について見ていきます。今回の作図について、パラメタ$a$は1を用います。
平板への写像による翼
パラメタ$r$が1、また$x$、$y$が共に0の場合を考えます。
ジューコフスキー変換の式より、写像された値は虚部を持たないことが分かります。つまり下図のような平板に写像されます。
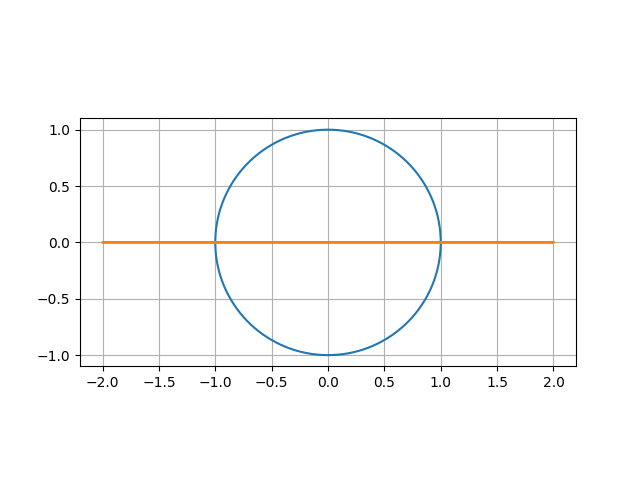
楕円状の翼
パラメタ$r$が1.1、また$x$、$y$が共に0の場合、下図のような楕円に写像されます。
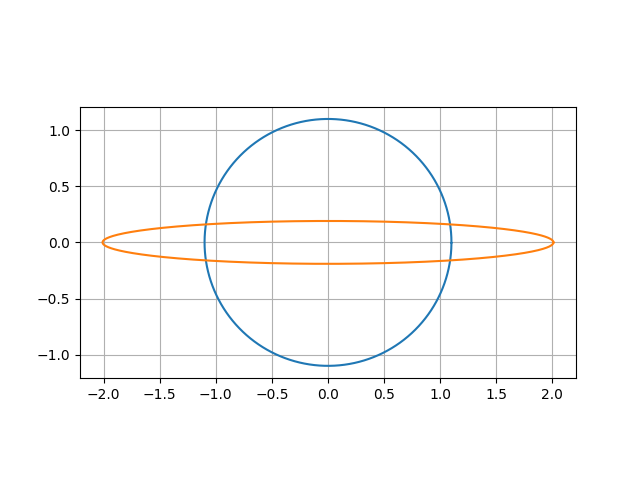
対称ジューコフスキー翼
パラメタ$r$が1.1、$y$が0の場合を考えます。$x$が0.1とすると、下図のような対称翼となり、これを対称ジューコフスキー翼と呼びます。
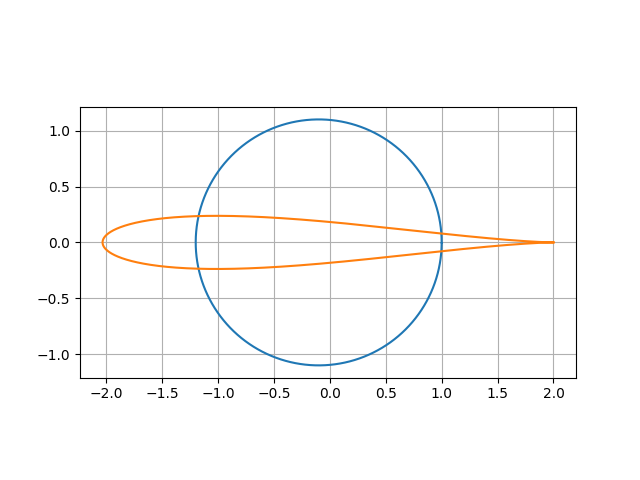
一般ジューコフスキー翼
下図は、パラメタ$r$を1.1、$x$を0.1、$y$を0.05としてプロットした翼型です。一般ジューコフスキー翼と呼びます。
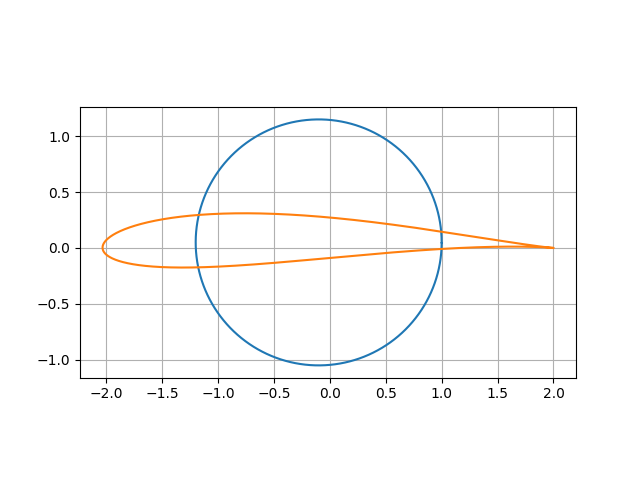
また、パラメタ$y$を0.1として同様にプロットすると、
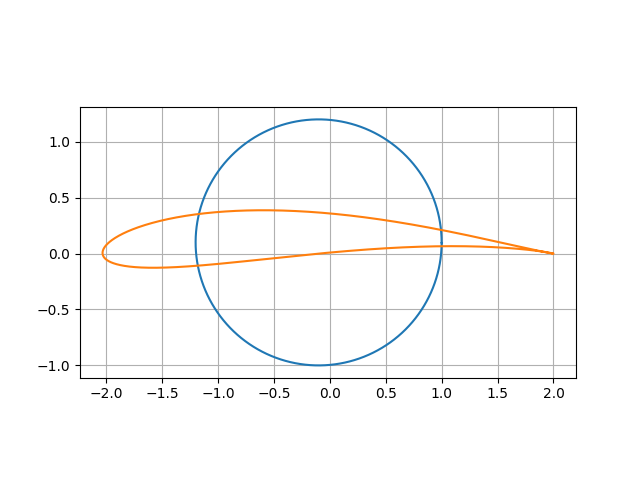
このような翼型が得られ、またパラメタ$y$を0.15とすると、
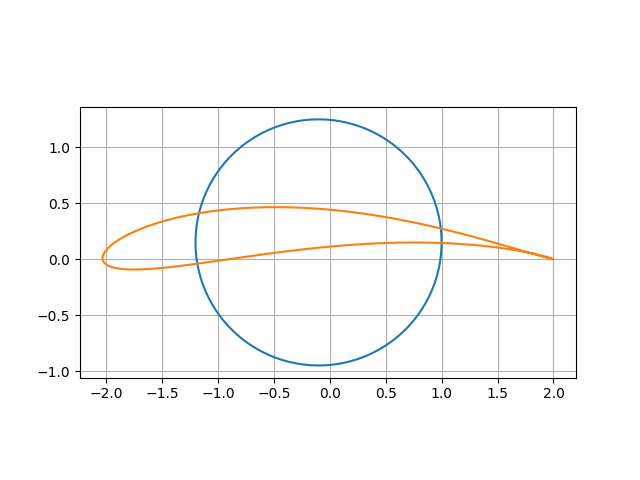
という翼型が得られます。
つまり、写像前の円の中心点$(x,y)$の$y$が大きいほど、反った形状の翼になります。
終わりに
このようにちゃんとまとめた記事を書くのは初めてです。
レベルは低いかもしれませんが、記事を書いて、プログラムを動かして、結果をまとめるという流れはとても楽しかったです。yapattaさんアドベントカレンダーの企画ありがとうございました〜〜!
ここまで読んでくれてありがとうございます!
参考文献
・牧野光雄『航空力学の基礎』産業図書,2012
・八田夏夫『基礎流体力学』恒星社,2003