Pythonで投資先の理想のポートフォリオを検証してみた

##自己紹介
プラントメーカに８年間→AIdemyを受講

##目的
米国株、金、石油、長期国債などのマーケットはサイクルで価格変動する”季節性”が存在すると言われている。そのため、リスク回避が必要であり、投資をする際、投資先のポートフォリオを考える必要がある。
米国株、金、石油、長期国債の実績データからどのようなポートフォリオが良いか、分析してみた。

##流れ
⑴米国株、金、石油、長期国債のデータを取得する
↓
⑵米国株、金、石油、長期国債の各々正規化して比較できるよう整える
↓
⑶米国株、金、石油、長期国債の相関行列を作成し、関係性の強い指標を主成分分析するとともにグラフ化して考察する。

まず、米国株、金、石油、長期国債指標について検証するにあたり、下記データを使用する。
米国株指標：NYダウ(^DJI)
金価格指標：iShares COMEX Gold Trust(IAU)
石油価格指標：United States Oil Fund(USO)
長期国債指標：iShares 20+ yr Treasury(TLT)

###⑴米国株、金、石油、長期国債のデータを取得する
pandasを用いて、yahooから各々のデータを取得する。
その際、前日終値(Adj Close)だけを取得するコードとした。

import pandas_datareader.data as web

tsd1 = web.DataReader("^DJI","yahoo","2011/6/16").dropna()
tsd1_Adj = tsd1.loc[:, 'Adj Close']
tsd2 = web.DataReader("IAU","yahoo","2011/6/16").dropna()
tsd2_Adj = tsd2.loc[:, 'Adj Close']
tsd3 = web.DataReader("USO","yahoo","2011/6/16").dropna()
tsd3_Adj = tsd3.loc[:, 'Adj Close']
tsd4 = web.DataReader("TLT","yahoo","2011/6/16").dropna()
tsd4_Adj = tsd4.loc[:, 'Adj Close']

tsd1_Adj
tsd2_Adj
tsd3_Adj
tsd4_Adj

###結果

Date
2011-06-16     75.842728
2011-06-17     75.484398
2011-06-20     75.577858
2011-06-21     75.242897
2011-06-22     75.289658
                 ...    
2021-06-11    142.309998
2021-06-14    141.220001
2021-06-15    141.050003
2021-06-16    140.929993
2021-06-17    142.225998
Name: Adj Close, Length: 2518, dtype: float64

###⑵米国株、金、石油、長期国債の各々正規化して比較できるよう整える
sklearnを用いて、0-1のスケールで各々のデータを比較できるように
正規化した。

import pandas as pd
from sklearn.preprocessing import MinMaxScaler

data_tsd1 = pd.DataFrame(tsd1_Adj)
scaler = MinMaxScaler([0,1])
scaler.fit(data_tsd1)
data_MinMaxScaler1 = scaler.transform(data_tsd1)
data_MinMaxScaler1

data_tsd2 = pd.DataFrame(tsd2_Adj)
scaler.fit(data_tsd2)
data_MinMaxScaler2 = scaler.transform(data_tsd2)
data_MinMaxScaler2

data_tsd3 = pd.DataFrame(tsd3_Adj)
scaler.fit(data_tsd3)
data_MinMaxScaler3 = scaler.transform(data_tsd3)
data_MinMaxScaler3

data_tsd4 = pd.DataFrame(tsd4_Adj)
scaler.fit(data_tsd4)
data_MinMaxScaler4 = scaler.transform(data_tsd4)
data_MinMaxScaler4

###⑶米国株、金、石油、長期国債の季節性を確認する
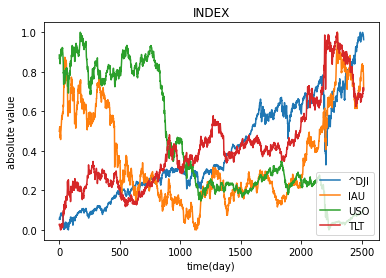
matplotlib.pyplotを用いて、各々のデータをグラフ化した。

%matplotlib inline 
import matplotlib.pyplot as plt

plt.title("INDEX")
plt.xlabel("time(day)")
plt.ylabel("absolute value")
plt.plot(data_MinMaxScaler1, label='^DJI')
plt.plot(data_MinMaxScaler2, label='IAU')
plt.plot(data_MinMaxScaler3, label='USO')
plt.plot(data_MinMaxScaler4, label='TLT')
plt.legend(loc='lower right')
plt.show()

結果

各々のデータの関係性を調べるため、numpyを用いて、相関行列を作成する。

import numpy as np

X = np.concatenate([data_MinMaxScaler1, data_MinMaxScaler2, data_MinMaxScaler3, data_MinMaxScaler4], axis=1)
R = np.corrcoef(X.T)

R

結果

	^DJI	IAU	USO	TLT
^DJI	1	0.1175043	-0.79141803	0.78686802
IAU	0.1175043	1	0.07655564	0.35164557
USO	-0.79141803	0.07655564	1	-0.82353141
TLT	0.78686802	0.35164557	-0.82353141	1

上記より、以下の指標の関係性が強いと想定する。
①米国株、石油価格
②米国株、長期国債
③石油価格、長期国債

次いで、上記①②③について、主成分分析(PCA)を用いて検証する。

①米国株、石油価格

import pandas as pd
from sklearn.decomposition import PCA

X1 = np.concatenate([data_MinMaxScaler1, data_MinMaxScaler3], axis=1)
pca=PCA(n_components=1)
X1_pca=pca.fit_transform(X1)

plt.title("INDEX")
plt.xlabel("time(day)")
plt.ylabel("absolute value")
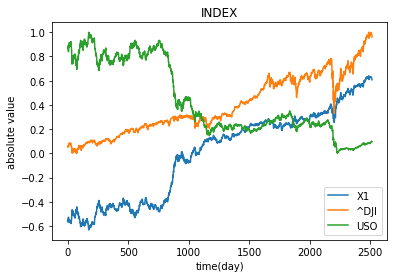
plt.plot(X1_pca, label='X1')
plt.plot(data_MinMaxScaler1, label='^DJI')
plt.plot(data_MinMaxScaler3, label='USO')
plt.legend(loc='lower right')
plt.show()

結果

考察
米国株と石油価格の関係性について、関係性が見てとれない。

②米国株、長期国債

X2 = np.concatenate([data_MinMaxScaler1, data_MinMaxScaler4], axis=1)
pca=PCA(n_components=1)
X2_pca=pca.fit_transform(X2)

plt.title("INDEX")
plt.xlabel("time(day)")
plt.ylabel("absolute value")
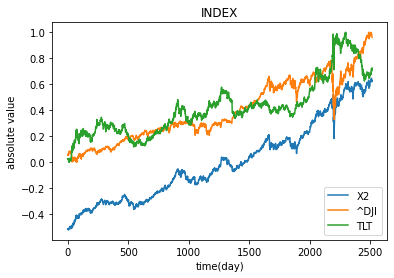
plt.plot(X2_pca, label='X2')
plt.plot(data_MinMaxScaler1, label='^DJI')
plt.plot(data_MinMaxScaler4, label='TLT')
plt.legend(loc='lower right')
plt.show()

結果

考察
米国株と長期国債の関係性について、
短期的な周期で反比例した動きが見られるが、長期的に両方の指標とも上昇方向であると
見てとれる。

③石油価格、長期国債

X3 = np.concatenate([data_MinMaxScaler3, data_MinMaxScaler4], axis=1)
pca=PCA(n_components=1)
X3_pca=pca.fit_transform(X3)

plt.title("INDEX")
plt.xlabel("time(day)")
plt.ylabel("absolute value")
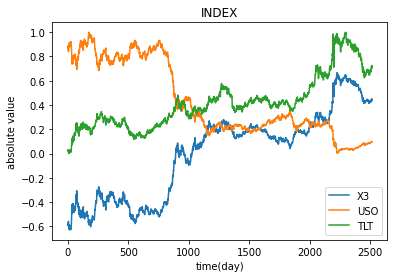
plt.plot(X3_pca, label='X3')
plt.plot(data_MinMaxScaler3, label='USO')
plt.plot(data_MinMaxScaler4, label='TLT')
plt.legend(loc='lower right')
plt.show()

結果

考察
石油価格と長期国債の関係性について、一貫して反比例した動きが見てとれる。

まとめると、、、
１）米国株と長期国債の関係性について、短期的な周期で反比例した動きが見られるが、長期的に両方の指標とも上昇方向である。
２）石油価格と長期国債の関係性について、一貫して反比例した動きが見られる。

##結果
今回の検証より、以下について考察することが出来た。
米国株と長期国債は長期的に上昇方向であり、投資すべきである。
但し、石油価格と長期国債が反比例した動きが見られるためリスク回避で石油価格も投資すべきである。

##今後の検証について
コモディティや他国指標などを追加して、さらなる関係性を見出していきたい。

##ちなみに、、、
米国株、金、石油、長期国債をまとめて主成分分析で２つの特徴に

pca=PCA(n_components=2)
X_pca=pca.fit_transform(X)

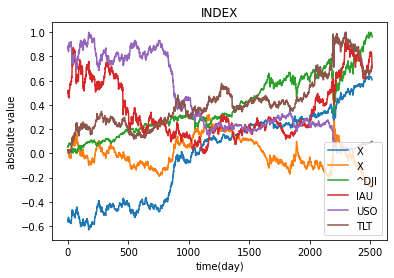
plt.title("INDEX")
plt.xlabel("time(day)")
plt.ylabel("absolute value")
plt.plot(X_pca, label='X')
plt.plot(data_MinMaxScaler1, label='^DJI')
plt.plot(data_MinMaxScaler2, label='IAU')
plt.plot(data_MinMaxScaler3, label='USO')
plt.plot(data_MinMaxScaler4, label='TLT')
plt.legend(loc='lower right')
plt.show()

比例と反比例の関係性が存在することが米国株、金、石油、長期国債の特徴として見られた。