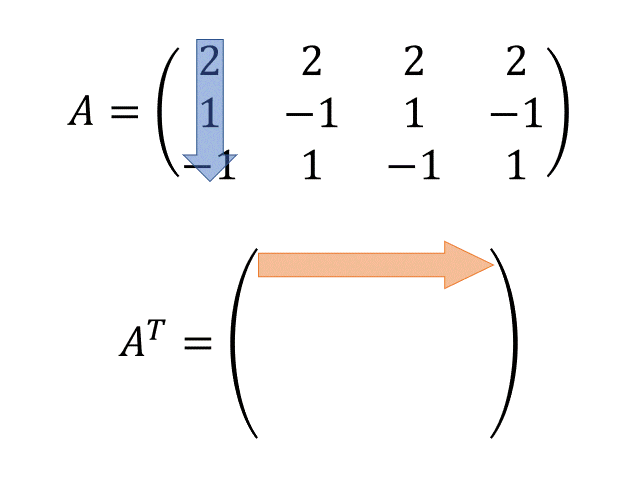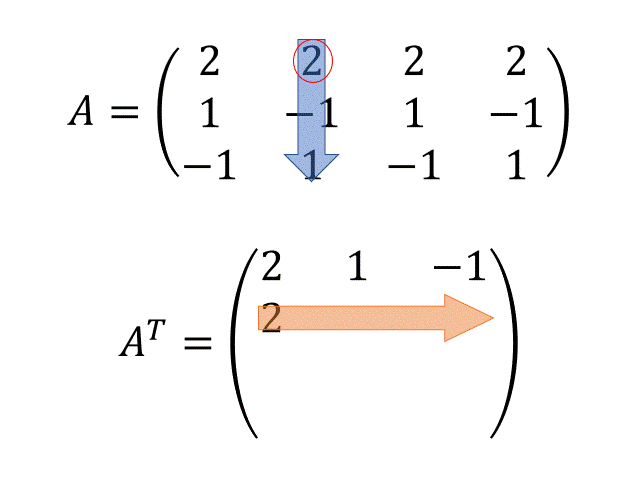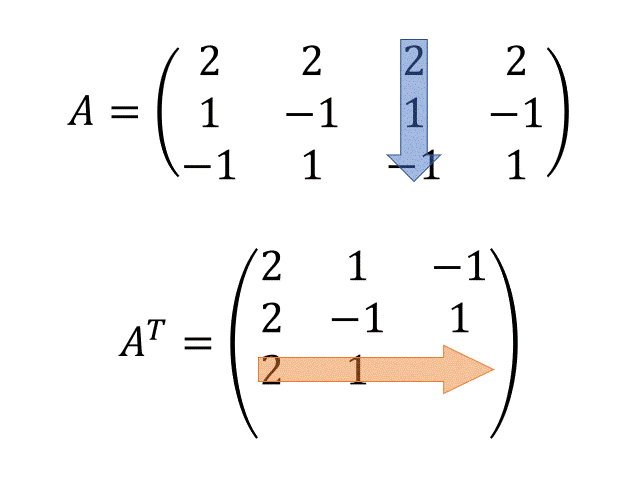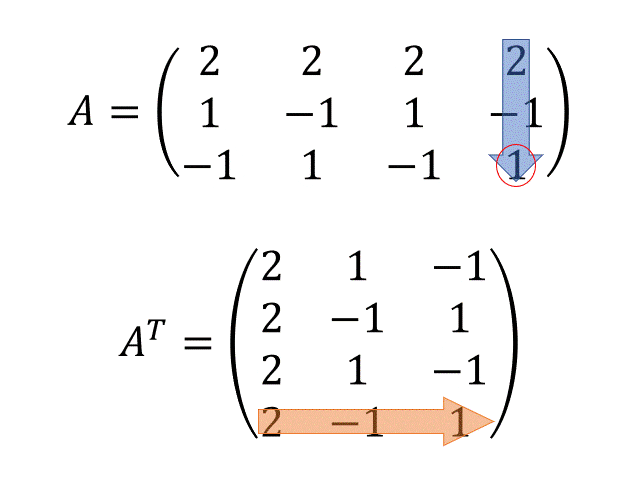特異値分解の計算方法を手順ごとにまとめてみた

はじめに

• E資格の数学問題で何かと話題の「特異値分解」。数式や社会への応用例については多くのサイトで解説されていますが、手計算でどうやって解いてくのか？を解説したものはあまり見かけないように思います。
  $$
  A = U \Sigma V^T
  $$
• なので、E資格数学の登竜門ともされる（と個人的に思う）特異値分解の手順を、自己流ながらまとめました。ここおかしい！というところがありましたらツッコミをお願いします。
• この記事は数学の計算過程を書いています。線形代数の行列に関する知識（ベクトルの内積、行列の和、積、行列式、固有値、固有ベクトル）に関する知識が必要です。

特異値分解の手計算の手順

特異値分解は線形代数の様々な計算法を使用します。これら1つでも間違うと正解を得ることができないので、
以下のステップごとに、着実にマスターしていく必要があります。

1. $U$、$\Sigma$、$V$の行列の形、大きさを把握する
   • $\Sigma$は$A$と同じ、$U$の大きさは行の個数の正方行列、$V$の大きさは列の個数の正方行列
2. 転置行列$A^T$を求める
   • GIFアニメでわかる転置行列の書き方
3. 行列積$A A^T$を求める
   • （横長の行列）×（縦長の行列）を計算するようにしよう！
4. 固有方程式$|AA^T-\lambda E| = 0$を解いて固有値$\lambda_1, \lambda_2$を求める
   • $AA^T-\lambda E$を計算しよう！
   • 行列式$|AA^T-\lambda E|$を計算しよう！
   • 因数分解して固有値$\lambda_1, \lambda_2$を求よう！
5. 求めた固有値$\lambda_1, \lambda_2$をもとに、固有ベクトル$\boldsymbol{u_1}, \boldsymbol{u_2}$を求める
   • 固有ベクトルの求め方
   • 求めた固有値と固有ベクトルは順番に並べる！
6. 残りのベクトル$\boldsymbol{u_3}$を求める。
   • 内積はゼロに$\boldsymbol{u_1} \cdot \boldsymbol{u_3} = 0$、$\boldsymbol{u_2} \cdot \boldsymbol{u_3} = 0$
   • 長さは1に$|\boldsymbol{u_3}|=1$
7. 固有値と固有ベクトルのペア$[\lambda_1, \boldsymbol{u_1}], [\lambda_2, \boldsymbol{u_2}]$から行列$V$の固有ベクトル$\boldsymbol{v_1}, \boldsymbol{v_2}$を求める
   • 固有ベクトルの左に転置行列を掛け$A^T u_i$とし、さらに固有値のルート$\sqrt{\lambda_i}$で割ってやる
   • 求めた固有値と固有ベクトルは順番に並べる！
8. 残りのベクトル$\boldsymbol{v_3}$と$\boldsymbol{v_4}$を求める
   • 内積はゼロ、長さは1
9. 最後に右側の行列$V$を転置させて$V^T$にする。
   • 転置行列に始まり、転置行列に終わる

行列$U$、$\Sigma$、$V^T$の数値が一部でもわかったら順次穴埋めしていくように進めます！

問題

• 以下のサイトの、具体例に書いてある行列を実際に解いてみようと思います！
  • 特異値分解の定義，性質，具体例 - 高校数学の美しい物語

A = \left(
\begin{array}{ccc}
2 & 2 & 2 & 2 \\
1 & -1 & 1 & -1 \\
-1 & 1 & -1 & 1
\end{array}
\right)

実際に解いてみる

1. U、Σ、Vの行列の形、大きさを把握する

• まずは最終的に出来上がる行列の形と大きさはどうなるのか？確認します。
  • まずは$\Sigma$の形状から。形状自体は、$A$と同じく3行4列の行列となります。
    $\Sigma$の中身は固有方程式の解$\lambda_i$の個数によって変わります。
• $\lambda_i$の解の個数が$\lambda_1$の1つだけの場合は・・・

\Sigma = 
\left(
\begin{array}{cccc}
\sqrt{\lambda_1} & 0 & 0 & 0 \\ 
0 & 0 & 0 & 0 \\ 
0 & 0 & 0 & 0
\end{array}
\right)

• $\lambda_i$の解の個数が$\lambda_1$と$\lambda_2$の2つある場合は・・・

\Sigma = \begin{pmatrix} \sqrt{\lambda_1} & 0 & 0 & 0 \\ 0 & \sqrt{\lambda_2} & 0 & 0 \\ 0 & 0 & 0 & 0\end{pmatrix}

• $\lambda_i$の解の個数が$\lambda_1$、$\lambda_2$、$\lambda_3$と3つある場合は・・・

\Sigma = \begin{pmatrix} \sqrt{\lambda_1} & 0 & 0 & 0 \\ 0 & \sqrt{\lambda_2} & 0 & 0 \\ 0 & 0 & \sqrt{\lambda_3} & 0\end{pmatrix}

• $\lambda_i$の値は正であること（$\lambda_i>0$）、行列$\Sigma$には$\lambda_i$の平方根の正の値$\sqrt{\lambda_i}$を入れることに注意しましょう！

• 次に$U$の形状です。$A$の行の個数が3であることから、$U$は3行3列の行列、つまり3次の正方行列となります。

U = \begin{pmatrix} u_{11} & u_{12} & u_{13} \\ u_{21} & u_{22} & u_{23} \\ u_{31} & u_{32} & u_{33} \end{pmatrix}

• 3つのベクトル$\boldsymbol{u_1} = \begin{pmatrix} u_{11} \ u_{21} \ u_{31} \end{pmatrix}$、$\boldsymbol{u_2} = \begin{pmatrix} u_{11} \ u_{21} \ u_{31} \end{pmatrix}$、$\boldsymbol{u_3} = \begin{pmatrix} u_{11} \ u_{21} \ u_{31} \end{pmatrix}$を用いて、$U$は3つのベクトルが組み合わせて出来た行列と考えてもOKです。

U = \begin{pmatrix} \boldsymbol{u_1} & \boldsymbol{u_2} & \boldsymbol{u_3}\end{pmatrix} = \begin{pmatrix} u_{11} & u_{12} & u_{13} \\ u_{21} & u_{22} & u_{23} \\ u_{31} & u_{32} & u_{33} \end{pmatrix}

• 最後に行列$V$の形状です。$A$の列の個数が4であることから、$V$は4行4列の行列、つまり4次の正方行列となります。
  $U$のときと同様に、ベクトル$\boldsymbol{v_1} = \begin{pmatrix} v_{11} \ v_{21} \ v_{31} \ v_{41} \end{pmatrix}$、$\boldsymbol{v_2} = \begin{pmatrix} v_{12} \ v_{22} \ v_{32} \ v_{42} \end{pmatrix}$、$\boldsymbol{v_3} = \begin{pmatrix} v_{13} \ v_{23} \ v_{33} \ v_{43} \end{pmatrix}$、$\boldsymbol{v_4} = \begin{pmatrix} v_{14} \ v_{24} \ v_{34} \ v_{44} \end{pmatrix}$で表してみます。

V = \begin{pmatrix} \boldsymbol{v_1} & \boldsymbol{v_2} & \boldsymbol{v_3} & \boldsymbol{v_4} \end{pmatrix} = \begin{pmatrix} v_{11} & v_{12} & v_{13} & v_{14} \\ v_{21} & v_{22} & v_{23} & v_{24} \\ v_{31} & v_{32} & v_{33} & v_{34} \\ v_{41} & v_{42} & v_{43} & v_{44} \end{pmatrix}

• 行列$U$と$V$の中身は当然何でも良いわけではありません。詳しくは「6. 残りのベクトル$\boldsymbol{u_3}$を求める」で説明します。
• 式の穴埋めをしていくような感じで、特異値分解の計算を1ステップずつやってみましょう！まずは行列$A$の転置行列$A^T$を求めてみます！

2. 転置行列A^Tを求める

• 転置行列$A^T$の書き方をGIFでアニメ化しました。
  

制作：はるなー＝ポッター

A^T = \begin{pmatrix} 2 & 1 & -1 \\ 2 & -1 & 1 \\ 2 & 1 & -1 \\ 2 & -1 & 1 \end{pmatrix}

3. 行列積AA^Tを求める

• （横長の行列）×（縦長の行列）にして計算しましょう！そうすることで、小さな正方行列にすることができます。

\begin{align*}
\\ AA^T &= \begin{pmatrix} 2 & 2 & 2 & 2 \\ 1 & -1 & 1 & -1 \\ -1 & 1 & -1 & 1 \end{pmatrix}
\begin{pmatrix} 2 & 1 & -1 \\ 2 & -1 & 1 \\ 2 & 1 & -1 \\ 2 & -1 & 1 \end{pmatrix} \\ \\
&= \begin{pmatrix} 2\times2+2\times2+2\times2+2\times2 & 2\times1+2\times(-1)+2\times1+2\times(-1) & 2\times(-1)+2\times1+2\times(-1)+2\times1\\
1\times2+(-1)\times2+1\times2+(-1)\times2 & 1\times1+(-1)\times(-1)+1\times1+(-1)\times(-1) & 1\times(-1)+(-1)\times1+1\times(-1)+(-1)\times1 \\
(-1)\times2+1\times2+(-1)\times2+1\times2 & (-1)\times1+1\times(-1)+(-1)\times1+1\times(-1) & (-1)\times(-1)+1\times1+(-1)\times(-1)+1\times1 \end{pmatrix} \\ \\
&= \begin{pmatrix} 16 & 0 & 0 \\ 0 & 4 & -4 \\ 0 & -4 & 4 \end{pmatrix} \\ \\
\end{align*}

• $AA^T$は3次の正方行列になりました。間違って（縦長の行列）×（横長の行列）となる$A^TA$を計算すると
  4次の正方行列となり、その後の計算がハードモードになります・・・

\begin{align*}
\\ A^TA &= \begin{pmatrix} 2 & 1 & -1 \\ 2 & -1 & 1 \\ 2 & 1 & -1 \\ 2 & -1 & 1 \end{pmatrix} \begin{pmatrix} 2 & 2 & 2 & 2 \\ 1 & -1 & 1 & -1 \\ -1 & 1 & -1 & 1 \end{pmatrix} \\ \\
&= \begin{pmatrix} 2\times2+1\times1+(-1)\times(-1) & 2\times2+1\times(-1)+(-1)\times1 & 2\times2+1\times1+(-1)\times(-1) & 2\times2+1\times(-1)+(-1)\times1 \\ 2\times2+(-1)\times1+1\times(-1) & 2\times2+(-1)\times(-1)+1\times1 & 2\times2+(-1)\times1+1\times(-1) & 2\times2+(-1)\times(-1)+1\times1 \\  2\times2+1\times1+(-1)\times(-1) & 2\times2+1\times(-1)+(-1)\times1 & 2\times2+1\times1+(-1)\times(-1) & 2\times2+1\times(-1)+(-1)\times1 \\ 2\times2+(-1)\times1+1\times(-1) & 2\times2+(-1)\times(-1)+1\times1 & 2\times2+(-1)\times1+1\times(-1) & 2\times2+(-1)\times(-1)+1\times1 \end{pmatrix} \\ \\
&= \begin{pmatrix} 6 & 2 & 6 & 2 \\ 2 & 6 & 2 & 6 \\ 6 & 2 & 6 & 2 \\ 2 & 6 & 2 & 6 \end{pmatrix} \\ \\
\end{align*}

• なので固有方程式を解くのに使うのは$AA^T$にしましょう！

4. 固有方程式|AA^T-λE|=0を解いて固有値λ_1、λ_2を求める

• まずは$AA^T-\lambda E$を計算します。

AA^T-\lambda E = \begin{pmatrix} 16 & 0 & 0 \\ 0 & 4 & -4 \\ 0 & -4 & 4 \end{pmatrix} - \begin{pmatrix} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \end{pmatrix} = \begin{pmatrix} 16-\lambda & 0 & 0 \\ 0 & 4-\lambda & -4 \\ 0 & -4 & 4-\lambda \end{pmatrix}

• 続いて固有方程式を解くために行列式$|AA^T-\lambda E|$を計算します。
  • 計算方法はたくみさんのYoutube動画を参考に
    【大学数学】行列式の求め方(テスト対策)【線形代数】 - 予備校のノリで学ぶ「大学の数学・物理」

\begin{align*}
\\ |AA^T-\lambda E| &= \left| \begin{array}{ccc} 16-\lambda & 0 & 0 \\ 0 & 4-\lambda & -4 \\ \\ 0 & -4 & 4-\lambda \end{array} \right| \\ \\ &= (16-\lambda)\times \left| \begin{array}{ccc} 4-\lambda & -4 \\ -4 & 4-\lambda \end{array} \right| - 0\times \left| \begin{array}{ccc} 0 & 0 \\ \\ -4 & 4-\lambda \end{array} \right| + 0\times \left| \begin{array}{ccc} 0 & 0 \\ 4-\lambda & -4 \end{array} \right| \\ \\ &= (16-\lambda)[(4-\lambda)^2 - (-4)^2] \\ \\ &= (16-\lambda)[(4-\lambda)+(-4)][(4-\lambda)-(-4)] \\ \\ &= (16-\lambda)(-\lambda)(8-\lambda) \\ \\
\end{align*}

• これで固有方程式$|AA^T-\lambda E| = 0$が求まります！
  $\lambda=0$や負の値は特異値分解での固有方程式の解じゃないので入れないようにしましょう！

\begin{align*}
|AA^T-\lambda E| &= (16-\lambda)(-\lambda)(8-\lambda) = 0 \\
\lambda_1,\lambda_2&=16, 8 \\
\end{align*}

• $\Sigma$の中身がこれで完全に分かりました。固有方程式の解の個数は2個なので、
  $\lambda_1$と$\lambda_2$を$\Sigma$に代入してみましょう！固有値は大きいもの順に並べるのが慣例みたいです。

\Sigma = \begin{pmatrix} \sqrt{\lambda_1} & 0 & 0 & 0 \\ 0 & \sqrt{\lambda_2} & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \sqrt{16} & 0 & 0 & 0 \\ 0 & \sqrt{8} & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} 4 & 0 & 0 & 0 \\ 0 & 2\sqrt{2} & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}

5. 求めた固有値λ_1、λ_2をもとに、固有ベクトルu_1、u_2を求める

• 固有ベクトルの求め方についてもたくみさんのYoutube動画で解説があります
  • 【大学数学】線形代数入門⑫(固有値・固有ベクトル) - 予備校のノリで学ぶ「大学の数学・物理」【線形代数】
  • 【大学数学】固有値・固有ベクトルの求め方(テスト対策)【線形代数】- 予備校のノリで学ぶ「大学の数学・物理」
• まずは$\lambda_1=16$のときの固有ベクトル$\boldsymbol{u_1}=\begin{pmatrix} u_{11} \ u_{21} \ u_{31} \end{pmatrix}$を求めてみましょう！
  • 固有方程式を計算します。

\begin{align*}
(AA^T - \lambda_1 E) &= \begin{pmatrix} 16 & 0 & 0 \\ 0 & 4 & -4 \\ 0 & -4 & 4 \end{pmatrix} - 16 \times \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 \\ 0 & -12 & -4 \\ 0 & -4 & -12 \end{pmatrix} \\ \\
(AA^T - \lambda_1 E) \boldsymbol{u_1} &= \begin{pmatrix} 0 & 0 & 0 \\ 0 & -12 & -4 \\ 0 & -4 & -12 \end{pmatrix} \begin{pmatrix} u_{11} \\ u_{21} \\ u_{31} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}
\end{align*}

• この固有方程式を連立方程式の形に整理してみます。

\begin{align*}
\begin{cases} 0\times u_{11} \quad + 0\times u_{21} &+ 0\times u_{31} &= 0 \\ 0\times u_{11} \quad + (-12)\times u_{21} &+ (-4)\times u_{31} &= 0 \\ 0\times u_{11} \quad + (-4)\times u_{21} &+ (-12)\times u_{31} &= 0 \end{cases}
\end{align*}

• 更に整理すると・・・

\begin{cases} 3u_{21} &+ u_{31} &= 0 \\ u_{21} &+ 3u_{31} &= 0 \end{cases}

• 連立方程式から$u_{21}=0$、$u_{31}=0$であることが分かりました。
  $u_{11}$については、どんな数値を入れても方程式が成立するので、任意の定数$c_1$を用いて$u_{11}=c_1$とします。
  これで$u_{11}$、$u_{21}$、$u_{31}$の解が求まりました！

\begin{pmatrix} u_{11} \\ u_{21} \\ u_{31} \end{pmatrix} = \begin{pmatrix} c_1 \\ 0 \\ 0 \end{pmatrix} = c_1\times \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}

• この式の内、定数$c_1$を除いた$\begin{pmatrix} 1 \ 0 \ 0 \end{pmatrix}$が固有ベクトル$\boldsymbol{u_1}$となります！

\boldsymbol{u_1}= \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}

• $\lambda_2=8$のときの固有ベクトル$\boldsymbol{u_2}=\begin{pmatrix} u_{12} \ u_{22} \ u_{32} \end{pmatrix}$も同じように計算します！

\begin{align*}
(AA^T - \lambda_2 E) &= \begin{pmatrix} 16 & 0 & 0 \\ 0 & 4 & -4 \\ 0 & -4 & 4 \end{pmatrix} - 8 \times \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 0 & 0 \\ 0 & -4 & -4 \\ 0 & -4 & -4 \end{pmatrix} \\ \\
(AA^T - \lambda_2 E) \boldsymbol{u_2} &= \begin{pmatrix} 8 & 0 & 0 \\ 0 & -4 & -4 \\ 0 & -4 & -4 \end{pmatrix} \begin{pmatrix} u_{12} \\ u_{22} \\ u_{32} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}
\end{align*}

• 連立方程式の形に整理します。

\begin{align*}
\begin{cases} 8\times u_{12} \quad + 0\times u_{22} &+ 0\times u_{32} &= 0 \\ 0\times u_{12} \quad + (-4)\times u_{22} &+ (-4)\times u_{32} &= 0 \\ 0\times u_{12} \quad + (-4)\times u_{22} &+ (-4)\times u_{32} &= 0 \end{cases} 
\end{align*}

• 更に整理すると・・・

\begin{align*}
\begin{cases} u_{12} &= 0 \\ u_{22}　&= -u_{32} \end{cases}
\end{align*}

• $u_{32}$については、$u_{22}$にマイナスを付けた値であれば、どんなものでもOKみたいです。先ほどと同じように任意の定数$c_2$を用いて、$u_{12}$、$u_{22}$、$u_{32}$の解を求めます。

\begin{pmatrix} u_{12} \\ u_{22} \\ u_{32} \end{pmatrix} = \begin{pmatrix} 0 \\ c_2 \\ -c_2 \end{pmatrix} = c_2\times \begin{pmatrix} 0 \\ 1 \\ -1 \end{pmatrix}

• 最後に、ベクトルの長さが1となるように定数$c_2$の数値を求めれば、2つ目の固有ベクトル$\boldsymbol{u_2}$の出来上がりです！
  ベクトル$\boldsymbol{u_2} = \begin{pmatrix} u_{12} \ u_{22} \ u_{32} \end{pmatrix} = \begin{pmatrix} 0 \ c_2 \ -c_2 \end{pmatrix}$の長さを1にするには、${u_{12}}^2 + {u_{22}}^2 + {u_{32}}^2 = 1$を満たす必要があります。

\begin{align*}
{u_{12}}^2 + {u_{22}}^2 + {u_{32}}^2 &= ({c_2\times 0})^2 + ({c_2\times 1})^2 + ({c_2\times (-1)})^2 \\ &= {c_2}^2 \times (0^2 + 1^2 + (-1)^2) \\ &= {c_2}^2\times 2 \\ &= 1 \\ {c_2}^2 &= \frac{1}{2} \\ c_2 &= \frac{1}{\sqrt{2}} \\
\end{align*}

• これでベクトル$\boldsymbol{u_2}$が以下のように求まりました！

\boldsymbol{u_2} = \frac{1}{\sqrt{2}} \times \begin{pmatrix} 0 \\ 1 \\ - 1 \end{pmatrix} = \begin{pmatrix} 0 \\ \frac{1}{\sqrt{2}} \\ - \frac{1}{\sqrt{2}} \end{pmatrix}

• 行列$U$の成分の一部がこれでわかりました。穴埋めしましょう！
  $\Sigma$に入れた固有値の順番通りに、対応する固有ベクトルを代入していきます。

U = \begin{pmatrix} \boldsymbol{u_1} &,& \boldsymbol{u_2} &,& \boldsymbol{u_3} \end{pmatrix} = \begin{pmatrix} \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} &,& \begin{bmatrix} 0 \\ \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{bmatrix} &,& \boldsymbol{u_3} \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & \frac{1}{\sqrt{2}}  &,& \boldsymbol{u_3} \\ 0 & -\frac{1}{\sqrt{2}} \end{pmatrix}

• 次は残りのベクトル$\boldsymbol{u_3}$を求めてみます。

6. 残りのベクトルu_3を求める

• $\boldsymbol{u_3}$については、下記の条件に基づいて方程式を解いていきます。

  1. $\boldsymbol{u_1}$と直交する（$\boldsymbol{u_1} \cdot \boldsymbol{u_3} = 0$）
  2. $\boldsymbol{u_2}$と直交する（$\boldsymbol{u_2} \cdot \boldsymbol{u_3} = 0$）
  3. ベクトルの長さ$|\boldsymbol{u_3}|$が1である

• 実際に解いてみましょう！

\boldsymbol{u_1} \cdot \boldsymbol{u_3} = u_{11}\times u_{13} + u_{21}\times u_{23} + u_{31}\times u_{33} = 1\times u_{13}+ 0\times u_{23} + 0\times u_{33} = 0

より、$u_{31}=0$が求まります。

\boldsymbol{u_2} \cdot \boldsymbol{u_3} = u_{12}\times u_{13} + u_{22}\times u_{23} + u_{32}\times u_{33} = 0\times u_{13}+ \frac{1}{\sqrt{2}} \times u_{23} + (-\frac{1}{\sqrt{2}}) \times u_{33} = 0

より、$\frac{1}{\sqrt{2}} \times u_{23} -\frac{1}{\sqrt{2}} u_{33} = 0$、つまり$u_{23}=u_{33}$で両者は等しいことが分かります。

|\boldsymbol{u_3}| = \sqrt{{u_{13}}^2 + {u_{23}}^2 + {u_{33}}^2} = \sqrt{0^2 + {u_{23}}^2 + {u_{23}}^2} = \sqrt{2{u_{23}}^2} = 1

より、${u_{23}}^2 = \frac{1}{2}$となり、$u_{23} = u_{33} = \frac{1}{\sqrt{2}}$であることが分かります。

• これで$\boldsymbol{u_3}$も求まりました！

\boldsymbol{u_3} = \begin{pmatrix} u_{13} \\ u_{23} \\ u_{33} \end{pmatrix} = \begin{pmatrix} 0 \\ \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix}

• これで行列$U$のすべてのベクトル$\boldsymbol{u_1}$、$\boldsymbol{u_2}$、$\boldsymbol{u_3}$がわかりました。穴埋めしましょう！

U = \begin{pmatrix} 1 & 0 \\ 0 & \frac{1}{\sqrt{2}}  &,& \boldsymbol{u_3} \\ 0 & -\frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & \frac{1}{\sqrt{2}}  &,& \begin{bmatrix} 0 \\ \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \\ 0 & -\frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 0 & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}

7. 固有値と固有ベクトルのペアλ_1, u_1とλ_2, u_2から行列 𝑉 の固有ベクトルv_1、v_2を求める

• 実は固有値から求めた2つのベクトル$\boldsymbol{u_1}$と$\boldsymbol{u_2}$を使って$\boldsymbol{v_1}$と$\boldsymbol{v_2}$をそれぞれ計算で求めることができます。
  下の式に$A^T$と固有値と対応する固有ベクトルを代入すれば簡単に計算できます。

\boldsymbol{v_i} = \frac{1}{\sqrt{\lambda_i}} A^T \boldsymbol{u_i}

• 参考:ビッグデータの計算科学 第3–4回線形代数の基礎京都大学 大学院情報学研究科 数理工学専攻/高度情報教育基盤コア準備室關戸 啓人
  （82ページ目、右下の番号だと81番目です。膨大な枚数の講義資料・・・さすがは京都大・・・）

• 実際に計算してみましょう！

\begin{align*}
\boldsymbol{v_1} &= \frac{1}{\sqrt{\lambda_1}} A^T \boldsymbol{u_1} = \frac{1}{\sqrt{16}} \begin{pmatrix} 2 & 1 & -1 \\ 2 & -1 & 1 \\ 2 & 1 & -1 \\ 2 & -1 & 1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \frac{1}{4} \begin{pmatrix} 2 \\ 2 \\ 2 \\ 2 \end{pmatrix} = \begin{pmatrix} \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \end{pmatrix} \\ \\
\boldsymbol{v_2} &= \frac{1}{\sqrt{\lambda_2}} A^T \boldsymbol{u_2} = \frac{1}{\sqrt{8}} \begin{pmatrix} 2 & 1 & -1 \\ 2 & -1 & 1 \\ 2 & 1 & -1 \\ 2 & -1 & 1 \end{pmatrix} \begin{pmatrix} 0 \\ \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{pmatrix} = \frac{1}{2\sqrt{2}} \begin{pmatrix} \sqrt{2} \\ -\sqrt{2} \\ \sqrt{2} \\ -\sqrt{2} \end{pmatrix} = \begin{pmatrix} \frac{1}{2} \\ -\frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \end{pmatrix}
\end{align*}

• 行列$V$の成分の一部がわかりましたので、早速穴埋めしましょう！
  $\Sigma$に入れた固有値の順番通りに、対応する固有ベクトルを代入していきます。

V = \begin{pmatrix} \boldsymbol{v_1} &,& \boldsymbol{v_2} &,& \boldsymbol{v_3} &,& \boldsymbol{v_4} \end{pmatrix} = \begin{pmatrix} \begin{bmatrix} \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \end{bmatrix} &,& \begin{bmatrix} \frac{1}{2} \\ -\frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \end{bmatrix} &,& \boldsymbol{v_3} &,& \boldsymbol{v_4} \end{pmatrix} = \begin{pmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} &,& \boldsymbol{v_3} &,& \boldsymbol{v_4} \\ \frac{1}{2} & -\frac{1}{2} \end{pmatrix}

8. ベクトルv_3とv_4を求める

• 「6. 残りのベクトル$\boldsymbol{u_3}$を求める」と同様、$\boldsymbol{v_3}$と$\boldsymbol{v_4}$を求めてみます。$\boldsymbol{v_2} = \begin{pmatrix} \frac{1}{2} \ -\frac{1}{2} \ \frac{1}{2} \ -\frac{1}{2} \end{pmatrix}$のように、
  マイナスを2つ付けてしまえば、簡単に$\boldsymbol{v_3}$と$\boldsymbol{v_4}$が求まるんじゃないでしょうか？やって確かめてみましょう。
  • $\boldsymbol{v_3}$は1行目と4行目の成分をマイナスにしてみます。

\boldsymbol{v_3} = \begin{pmatrix} -\frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \end{pmatrix}

• ベクトルの内積$\boldsymbol{v_1} \cdot \boldsymbol{v_3} = 0$と$\boldsymbol{v_2} \cdot \boldsymbol{v_3} = 0$を満たし、条件を満たしていると分かります。

\boldsymbol{v_1} \cdot \boldsymbol{v_3} = \frac{1}{2} \times (-\frac{1}{2}) + \frac{1}{2} \times \frac{1}{2} + \frac{1}{2} \times \frac{1}{2} + \frac{1}{2} \times (-\frac{1}{2}) = -\frac{1}{4} + \frac{1}{4} + \frac{1}{4} - \frac{1}{4} = 0 \\
\boldsymbol{v_2} \cdot \boldsymbol{v_3} = \frac{1}{2} \times (-\frac{1}{2}) + (-\frac{1}{2}) \times \frac{1}{2} + \frac{1}{2} \times \frac{1}{2} + (-\frac{1}{2}) \times (-\frac{1}{2}) = -\frac{1}{4} - \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = 0

• もう1つの条件、ベクトルの長さが1も満たしています（$|\boldsymbol{v_3}| = 1$）。

|\boldsymbol{v_3}| = \sqrt{(-\frac{1}{2})^2 + (\frac{1}{2})^2 + (\frac{1}{2})^2 + (-\frac{1}{2})^2} = \sqrt{\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4}} = 1

• なので適当に2つの成分をマイナスにした$\boldsymbol{v_3}$は条件に適合してるので問題なく使えそうです！

\boldsymbol{v_3} = \begin{pmatrix} -\frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \end{pmatrix}

• $\boldsymbol{v_4}$も同様にして1行目と3行目の成分をマイナスにしてみます。

\boldsymbol{v_4} = \begin{pmatrix} -\frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \\ \frac{1}{2} \end{pmatrix} \\
\boldsymbol{v_2} \cdot \boldsymbol{v_4} = \frac{1}{2} \times (-\frac{1}{2}) + (-\frac{1}{2}) \times \frac{1}{2} + \frac{1}{2} \times (-\frac{1}{2}) + (-\frac{1}{2}) \times \frac{1}{2} = -\frac{1}{4} - \frac{1}{4} - \frac{1}{4} - \frac{1}{4} = -1

• これは$\boldsymbol{v_2}$と$\boldsymbol{v_4}$とが直交せずダメでした・・・。気を取り直して、3行目と4行目をマイナスにしたものはどうでしょうか？

\boldsymbol{v_4} = \begin{pmatrix} \frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \\ -\frac{1}{2} \end{pmatrix} \\
\boldsymbol{v_1} \cdot \boldsymbol{v_4} = \frac{1}{2} \times \frac{1}{2} + \frac{1}{2} \times \frac{1}{2} + \frac{1}{2} \times (-\frac{1}{2}) + \frac{1}{2} \times (-\frac{1}{2}) = \frac{1}{4} + \frac{1}{4} - \frac{1}{4} - \frac{1}{4} = 0 \\
\boldsymbol{v_2} \cdot \boldsymbol{v_4} = \frac{1}{2} \times \frac{1}{2} + (-\frac{1}{2}) \times \frac{1}{2} + \frac{1}{2} \times (-\frac{1}{2}) + (-\frac{1}{2}) \times (-\frac{1}{2}) = \frac{1}{4} - \frac{1}{4} - \frac{1}{4} + \frac{1}{4} = 0 \\
\boldsymbol{v_3} \cdot \boldsymbol{v_4} = (-\frac{1}{2}) \times \frac{1}{2} + \frac{1}{2} \times \frac{1}{2} + \frac{1}{2} \times (-\frac{1}{2}) + (-\frac{1}{2}) \times (-\frac{1}{2}) = -\frac{1}{4} + \frac{1}{4} - \frac{1}{4} + \frac{1}{4} = 0 \\
|\boldsymbol{v_4}| = \sqrt{(\frac{1}{2})^2 + (\frac{1}{2})^2 + (-\frac{1}{2})^2 + (-\frac{1}{2})^2} = \sqrt{\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4}} = 1

• $\boldsymbol{v_4}$は$\boldsymbol{v_4} = \begin{pmatrix} \frac{1}{2} \ \frac{1}{2} \ -\frac{1}{2} \ -\frac{1}{2} \end{pmatrix}$とするのが良いことが分かりました。

• これで行列$V$も求めることができました！

V = \begin{pmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} &,& \boldsymbol{v_3} &,& \boldsymbol{v_4} \\ \frac{1}{2} & -\frac{1}{2} \end{pmatrix} = \begin{pmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} &,& \begin{bmatrix} -\frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \end{bmatrix} &,& \begin{bmatrix} \frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \\ -\frac{1}{2} \end{bmatrix} \\ \frac{1}{2} & -\frac{1}{2} \end{pmatrix} = \begin{pmatrix} \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \end{pmatrix}

9. 最後に右側の行列Vを転置させてV^Tにする。

• これまでの計算結果から、$U$、$\Sigma$、$V$をまとめます。

U = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 0 & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} ,\quad
\Sigma = \begin{pmatrix} 4 & 0 & 0 & 0 \\ 0 & 2\sqrt{2} & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} ,\quad
V = \begin{pmatrix} \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \end{pmatrix}

• あとは転置行列$V^T$を求めるだけです。最後の総仕上げに入りましょう！

\boldsymbol{V}^T = \begin{pmatrix} \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \end{pmatrix}^T = \begin{pmatrix} \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \end{pmatrix}

• これで特異値分解の計算がようやく終わりました。計算結果は下の通りです！

\boldsymbol{A} = U \Sigma V^T = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 0 & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 4 & 0 & 0 & 0 \\ 0 & 2\sqrt{2} & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \end{pmatrix}

あれっ！？なんかちょっと違う・・・

• では問題元の高校数学の美しい物語のサイトで書かれた回答と答え合わせしましょう！
• 「高校数学の美しい物語」で書かれている答え

\boldsymbol{A} = U \Sigma V^T = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 0 & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 4 & 0 & 0 & 0 \\ 0 & 2\sqrt{2} & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \end{pmatrix}

• 計算結果

\boldsymbol{A} = U \Sigma V^T = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 0 & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 4 & 0 & 0 & 0 \\ 0 & 2\sqrt{2} & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \end{pmatrix}

• $V^T$のところが合ってないやないかい！とツッコミを入れたいところですが、行列積を計算して、$A$として合っていればよろしいんじゃないでしょうか？
  計算結果が実際に$A = \begin{pmatrix} 2 & 2 & 2 & 2 \ 1 & -1 & 1 & -1 \ -1 & 1 & -1 & 1 \end{pmatrix}$　になるのか確かめて見たいと思います。
  PythonのNumpyで計算してみます！

import numpy as np

U = np.array([
    [1.0,             0.0,            0.0],
    [0.0,  1.0/np.sqrt(2), 1.0/np.sqrt(2)],
    [0.0, -1.0/np.sqrt(2), 1.0/np.sqrt(2)]
])

S = np.array([
    [4.0,          0.0, 0.0, 0.0],
    [0.0, 2*np.sqrt(2), 0.0, 0.0],
    [0.0,          0.0, 0.0, 0.0]
])

V_T = np.array([
    [ 0.5,  0.5,  0.5,  0.5],
    [ 0.5, -0.5,  0.5, -0.5],
    [-0.5,  0.5,  0.5, -0.5],
    [ 0.5,  0.5, -0.5, -0.5]
])

print(f'U=\n{U}\n\nSigma=\n{S}\n\nV_T=\n{V_T}')

U=
[[ 1. 0. 0. ]
[ 0. 0.70710678 0.70710678]
[ 0. -0.70710678 0.70710678]]

Sigma=
[[4. 0. 0. 0. ]
[0. 2.82842712 0. 0. ]
[0. 0. 0. 0. ]]

V_T=
[[ 0.5 0.5 0.5 0.5]
[ 0.5 -0.5 0.5 -0.5]
[-0.5 0.5 0.5 -0.5]
[ 0.5 0.5 -0.5 -0.5]]

US = np.dot(U, S)
print(US)

[[ 4. 0. 0. 0.]
[ 0. 2. 0. 0.]
[ 0. -2. 0. 0.]]

A = US.dot(V_T)
print(A)

[[ 2. 2. 2. 2.]
[ 1. -1. 1. -1.]
[-1. 1. -1. 1.]]

• 計算すれば合っていることがわかります。実は、固有値から求めなかった2つのベクトル$\boldsymbol{v_3}$と$\boldsymbol{v_4}$はいろんなベクトルにできます。固有ベクトル$u_2$についても、$c_2$を負の値$-\frac{1}{\sqrt{2}}$とし、$u_2 = \begin{pmatrix} 0 \ -\frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}} \end{pmatrix}$にするのも間違いではありません。
  特異値分解の答えは1つとは限らないんです。シュミットの直交化の条件を満たし、$A$の計算が合えば無問題。そんな風に考えてください。

終わりに

• 実際に計算してみると分かりますが、特異値分解の計算は結構時間がかかります。
  まずは固有値、固有ベクトルまでをマスターしましょう（じゃないと特異値分解のところでE資格の試験時間が削られちゃいます・・・）。
• 2020#1のE資格試験では、特異値分解の問題が、・・・なんと！、・・・なんとおぉ！！・・・出ませんでした～ww（羽鳥慎一アナ風）
  • 固有値の問題（固有ベクトルもだったかな？）は出題されましたので、特異値分解の問題を解く練習が重要であることに変わりはないと思います。
    この記事がディープラーニング数学問題の手助けになれば幸いです。

参考サイトまとめ

• 特異値分解の問題元：特異値分解の定義，性質，具体例 - 高校数学の美しい物語
• GIFアニメ：PowerPointでGIFアニメを作る方法。スライドショーをパラパラマンガのように表現できる - できるネット
• 行列式の計算：【大学数学】行列式の求め方(テスト対策)【線形代数】 - 予備校のノリで学ぶ「大学の数学・物理」
• 固有値と固有ベクトルの計算：
  【大学数学】線形代数入門⑫(固有値・固有ベクトル) - 予備校のノリで学ぶ「大学の数学・物理」【線形代数】
  【大学数学】固有値・固有ベクトルの求め方(テスト対策)【線形代数】- 予備校のノリで学ぶ「大学の数学・物理」
• $\boldsymbol{v_1}$を固有方程式を使わず$\boldsymbol{u_1}$から計算する方法：ビッグデータの計算科学 第3–4回線形代数の基礎京都大学 大学院情報学研究科 数理工学専攻/高度情報教育基盤コア準備室關戸 啓人