はじめに
「Kaggleで勝つデータ分析の技術」のP372~373で紹介されている良いスタッキングのソリューション/スタッキングに含めるモデル選択を参考にして、Kaggleのチュートリアル(タイタニック)を題材にOptunaで各モデルのハイパーパラメータを調整していき予測モデルを作成しました。
▼多様なモデルを使う(Kaggleで勝つデータ分析の技術 p372により引用)
Kaggle GrandmasterのKazAnovaによると、良いスタッキングのソリューションは以下のモデルを含んで構成されることがたびたびあるとのことです。
・2~3つのGBDT(決定木の深さが浅いもの、中くらいのもの、深いもの)
・1~2つのランダムフォレスト(決定木の深さが浅いもの、深いもの)
・1~2つのニューラルネットワーク(1つは層の数が多いもの、1つは少ないもの)
・1つの線形モデル
▼スタッキングに含めるモデルの選択(Kaggleで勝つデータ分析の技術 p373により引用)
相関係数が0.95以下かつ、2つの母集団の確率分布が異なるかを検定するコルモゴロフ-スミルノフ検定統計量が0.05以上のモデルを、精度が高い順に選ぶという手法もあります。
GBDT・ニューラルネットワークを使用したスタッキングの実装は汎用性が高いかなと思いまして、今回作成したコードをもとに実装をメインとした記事を公開いたします。
OptunaやPyTorchを活用したニューラルネットワークの実装については、キカガクの脱ブラックボックスコースを参考にしています。
交差検証しながらOptunaでハイパーパラメータを調整してスタッキングする実装は、個人的には試行錯誤しながらとても苦労したので、少しでもご参考になることがあれば幸いです。
使用するライブラリ
まずは必要なライブラリを読み込みます。
# おなじみのライブラリ
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# scikit-learn
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold, cross_val_score
from sklearn.metrics import log_loss
from sklearn.metrics import accuracy_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
# Optuna
import optuna
# GBDT
import xgboost as xgb
# Pytorch
import torch
import torch.nn as nn
import torch.nn.functional as F
import pytorch_lightning as pl
from pytorch_lightning.metrics.functional import accuracy
from pytorch_lightning.callbacks import EarlyStopping
# モデルの保存・呼び出しで使用
import pickle
# コルモゴロフ-スミルノフ検定統計量
from scipy.stats import ks_2samp
データの確認
kaggleのTitanic - Machine Learning from Disasterから訓練データ・テストデータをダウンロードします。前処理・特徴量データ作成を訓練データ・テストデータで分けずにまとめてやるためにデータを結合します。
結合したデータをもとに欠損値の有無などを確認していきます。
# データを結合できるように、testデータにもSurvivedのカラムを追加する
train_data = pd.read_csv('train.csv')
test_data = pd.read_csv('test.csv')
test_data['Survived'] = np.nan
# 前処理、特徴量作成を一度にやるためにtrainデータとtestデータを結合する
dataset = pd.concat([train_data, test_data], ignore_index=True, sort=False)
# データの確認
dataset.info()
▼データの中身
欠損値があるカラムが確認できます。
このあと、欠損値は平均値・頻出値・予測値などで埋めていきます。
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1309 entries, 0 to 1308
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 PassengerId 1309 non-null int64
1 Survived 891 non-null float64
2 Pclass 1309 non-null int64
3 Name 1309 non-null object
4 Sex 1309 non-null object
5 Age 1046 non-null float64
6 SibSp 1309 non-null int64
7 Parch 1309 non-null int64
8 Ticket 1309 non-null object
9 Fare 1308 non-null float64
10 Cabin 295 non-null object
11 Embarked 1307 non-null object
dtypes: float64(3), int64(4), object(5)
memory usage: 122.8+ KB
前処理、特徴量の作成
age(年齢)は、欠損値がないデータをもとに予測して欠損値を埋めていきます。
# 欠損値がないデータを用意
dataset_age = dataset[['Age', 'Pclass','Sex', 'SibSp', 'Parch']]
# dataset_ageをワンホットエンコーディングする
dataset_age = pd.get_dummies(dataset_age)
# 学習データ用にnumpyに変換し、訓練データ・テストデータに分割する
dataset_age_known = dataset_age[dataset_age['Age'].notnull()].values
dataset_age_unknown = dataset_age[dataset_age['Age'].isnull()].values
x_train_age = dataset_age_known[:, 1:]
y_train_age = dataset_age_known[:, 0]
x_test_age = dataset_age_unknown[:, 1:]
# 訓練データをtrain/valに分割
X_train, X_val, y_train, y_val = train_test_split(x_train_age, y_train_age, test_size=0.2, random_state=0)
# xgboostでモデル作成・学習
dtrain_age = xgb.DMatrix(X_train, label=y_train)
dvalid_age = xgb.DMatrix(X_val, label=y_val)
param = {
'max_depth':2,
'eta':0.05,
'objective':'reg:squarederror',
'random_state':0
}
num_round = 1000
watchlist = [(dtrain_age, 'train'), (dvalid_age, 'eval')]
model_xgb_age = xgb.train(param, dtrain_age, num_round, evals=watchlist, early_stopping_rounds=50, verbose_eval=0)
# 予測データを作成し、欠損値を埋める
dtest_age = xgb.DMatrix(x_test_age)
pred_test = model_xgb_age.predict(dtest_age)
predict_age = pred_test.reshape(-1,1)
dataset.loc[(dataset['Age'].isnull()), 'Age' ] = predict_age
そのほかの欠損値対応や特徴量の作成については、以下にまとめました。
# 結婚女性
dataset['Title'] = dataset['Name'].str.extract('([A-Za-z]+)[.]', expand=False)
dataset['Is_Married'] = 0
dataset.loc[(dataset['Title'] == 'Mrs'),'Is_Married'] = 1
# 敬称を更にまとめる
dataset['Title'] = dataset['Title'].replace(['Miss', 'Mrs','Ms', 'Mlle', 'Lady', 'Mme', 'the Countess', 'Countess', 'Dona'], 'Miss/Mrs/Ms')
dataset['Title'] = dataset['Title'].replace(['Dr', 'Col', 'Major', 'Jonkheer', 'Capt', 'Sir', 'Don', 'Rev'], 'Dr/Military/Noble/Clergy')
# ファーストネームごとの人数
dataset['First_Name'] = dataset['Name'].str.extract('([A-Za-z]+)[,]', expand=False)
dataset['First_Name_nom'] = dataset['First_Name'].map(dataset['First_Name'].value_counts())
# 同乗者の人数
dataset['Family_size'] = dataset['SibSp'] + dataset['Parch'] + 1
# チケット番号ごとの人数
dataset['Ticket_label_nom'] = dataset['Ticket'].map(dataset['Ticket'].value_counts())
# 運賃の欠損値を平均値で埋める
dataset['Fare'] = dataset['Fare'].fillna(dataset['Fare'].mean())
# 客室番号の頭文字
dataset['Cabin'] = dataset['Cabin'].fillna('Unknown')
dataset['Cabin_label'] = dataset['Cabin'].str.get(0)
# 出港地の欠損値を頻出値で埋める
dataset['Embarked'] = dataset['Embarked'].fillna(dataset['Embarked'].mode()[0])
# Cabinを4つのグループに分ける
dataset['Cabin_label'].replace(['A', 'B', 'C', 'T'], 'ABC', inplace=True)
dataset['Cabin_label'].replace(['D', 'E'], 'DE', inplace=True)
dataset['Cabin_label'].replace(['F', 'G'], 'FG', inplace=True)
# 年齢を5つのグループに分ける
dataset.loc[ dataset['Age'] <= 8, 'Age_label'] = 0
dataset.loc[(dataset['Age'] > 8) & (dataset['Age'] <= 16), 'Age_label'] = 1
dataset.loc[(dataset['Age'] > 16) & (dataset['Age'] <= 32), 'Age_label'] = 2
dataset.loc[(dataset['Age'] > 32) & (dataset['Age'] <= 48), 'Age_label'] = 3
dataset.loc[(dataset['Age'] > 48) & (dataset['Age'] <= 64), 'Age_label'] = 4
dataset.loc[ dataset['Age'] > 64, 'Age_label'] = 5
# 名前ごとの人数別グループを3つのグループに分ける
dataset.loc[(dataset['First_Name_nom'] ==1), 'First_Name_nom_label'] = 0
dataset.loc[(dataset['First_Name_nom'] >=2)&(dataset['First_Name_nom'] <=3), 'First_Name_nom_label'] = 1
dataset.loc[(dataset['First_Name_nom'] >=4)&(dataset['First_Name_nom'] <=5), 'First_Name_nom_label'] = 2
dataset.loc[(dataset['First_Name_nom'] >=6), 'First_Name_nom_label'] = 3
# 家族の人数別グループを3つのグループに分ける
dataset.loc[(dataset['Family_size'] ==1), 'Family_size_label'] = 0
dataset.loc[(dataset['Family_size'] >=2)&(dataset['Family_size'] <=4), 'Family_size_label'] = 1
dataset.loc[(dataset['Family_size'] >=5)&(dataset['Family_size'] <=7), 'Family_size_label'] = 2
dataset.loc[(dataset['Family_size'] >=8), 'Family_size_label'] = 3
# 料金を4つのグループに分ける
dataset.loc[ dataset['Fare'] <= 7.91, 'Fare_label'] = 0
dataset.loc[(dataset['Fare'] > 7.91) & (dataset['Fare'] <= 14.454), 'Fare_label'] = 1
dataset.loc[(dataset['Fare'] > 14.454) & (dataset['Fare'] <= 31), 'Fare_label'] = 2
dataset.loc[ dataset['Fare'] > 31, 'Fare_label'] = 3
# チケットナンバーが同じ人数別グループを3つのグループに分ける
dataset.loc[(dataset['Ticket_label_nom'] ==1), 'Ticket_label'] = 0
dataset.loc[(dataset['Ticket_label_nom'] >=2)&(dataset['Ticket_label_nom'] <=4), 'Ticket_label'] = 1
dataset.loc[(dataset['Ticket_label_nom'] >=5)&(dataset['Ticket_label_nom'] <=8), 'Ticket_label'] = 2
dataset.loc[(dataset['Ticket_label_nom'] ==11), 'Ticket_label'] = 3
# モデル作成用のデータに加工、カテゴリカルなデータはone-hot encodingを行う
df = dataset[['Survived', 'Is_Married','Pclass', 'Sex', 'Age_label', 'Fare_label', 'Embarked', 'Title', 'Family_size_label', 'Ticket_label', 'Cabin_label', 'First_Name_nom_label']]
df = pd.get_dummies(df, columns=['Sex', 'Age_label', 'Fare_label', 'Embarked', 'Title', 'Family_size_label', 'Ticket_label', 'Cabin_label', 'First_Name_nom_label'])
# dfをw訓練データとテストデータに分割
train_df = df[df['Survived'].notnull()]
test_df = df[df['Survived'].isnull()].drop('Survived', axis=1)
# numpyに変換
X = train_df.values[:, 1:]
y = train_df.values[:, 0]
t = test_df.values
ここでは割愛しますが、seabornなどで各データとSurvivedとの関係を可視化してみると面白いです。
タイタニックの特徴量作成は色々な方法がネット上にも公開されているので、それらもとても参考になります。
1層目のモデル作成
1層目は、以下のモデルを作成します。
- GBDT(max_depthが2、5、8の3つのモデル)
- ランダムフォレスト(max_depthが2、8の2つのモデル)
- ニューラルネットワーク
- ロジスティック回帰
それぞれ、ハイパーパラメータ/目的関数を定義して、
交差検証しながらモデル・予測値を作成していきます。
Optunaで作成したモデルの保存方法や必要な関数の理解、交差検証など、
以下の公式ページや記事も参考にしました。
▶モデルの保存 — Optuna 2.5.0 documentation
▶カテゴリカルなハイパーパラメータ — Optuna 2.5.0 documentation
▶Pythonでwith構文を使う方法
▶Pythonの文字列フォーマット(formatメソッドの使い方)
▶開発効率をあげる!Pythonでpickleを使う方法
▶[Python]Numpyデータの並べ替え ― argsort
▶sklearnの交差検証の種類とその動作
■ 1層目のモデル作成|GBDT
まずは、GBDTのモデル作成、予測値の作成をします。
以下記事を参考にしました。
▶XGBoostパラメータのまとめとランダムサーチ実装
▶xgboost で Feature Importance を算出する。
モデルの実装は以下コードとなります。
# model1-1: xgboostでoptunaでの調整をもとにモデルを作成し、クロスバリデーションで学習・予測を行い、予測値を得る
# max_depth = 2
# Optunaでハイパーパラメータを調整する
optuna.logging.disable_default_handler()
# optuna.logging.disable_default_handler()でログを非表示
# optuna.logging.enable_default_handler()でログを再度表示
def objective(trial):
#ハイパーパラメータの候補領域
param = {
'max_depth': 2,
'eta': trial.suggest_loguniform('eta', 1e-2, 1e-1),
'gamma': trial.suggest_uniform('gamma', 0, 1.0),
'min_child_weight': trial.suggest_uniform('min_child_weight', 1.0, 4.0),
'colsample_bytree': trial.suggest_uniform('colsample_bytree', 0.6, 0.95),
'subsample': trial.suggest_uniform('subsample', 0.6, 0.95),
'alpha': trial.suggest_uniform('alpha', 0, 10.0),
'lambda': trial.suggest_uniform('lambda', 0, 1.0),
'objective':'binary:logistic',
'eval_metric':'logloss',
'random_state':0
}
#ハイパーパラメータ以外の諸々設定
num_round = 2000
#early_stopping_rounds = trial.suggest_int('early_stopping_rounds', 10, 100)
early_stopping_rounds = 50
watchlist = [(dtrain, 'train'), (dvalid, 'eval')]
#目的関数の定義
#学習状況の表示回数 verbose_eval
#参考ページ https://potesara-tips.com/xgboost-holdout/
model_xgb = xgb.train(param, dtrain, num_round, evals=watchlist, early_stopping_rounds=early_stopping_rounds, verbose_eval=0)
#Save a trained model to a file.
with open("{}.pickle".format(trial.number), "wb") as fout:
pickle.dump(model_xgb, fout)
#バリデーションデータでモデルの評価(スコア確認)
pred_xgb = model_xgb.predict(dvalid)
loss = log_loss(y_val, pred_xgb)
return loss
# 予測値・インデックスの保存用リスト
preds_xgb = []
preds_test_xgb = []
va_idxes_xgb = []
# クロスバリデーションで学習・予測を行い、予測値とインデックスを保存する
kf = KFold(n_splits=5, shuffle=True, random_state=71)
for i, (tr_idx, va_idx) in enumerate(kf.split(X)):
tr_x_xgb, va_x_xgb = X[tr_idx], X[va_idx]
tr_y_xgb, va_y_xgb = y[tr_idx], y[va_idx]
#print(tr_idx.shape)
#print(va_idx.shape)
#sys.exit()
#訓練データ・バリデーションデータの分割
X_train, X_val, y_train, y_val = train_test_split(tr_x_xgb, tr_y_xgb, test_size=0.2, random_state=0)
dtrain = xgb.DMatrix(X_train, label=y_train, feature_names=train_df.columns[1:])
dvalid = xgb.DMatrix(X_val, label=y_val, feature_names=train_df.columns[1:])
#ハイパーパラメータの最適化
sampler = optuna.samplers.TPESampler(seed=0)
study = optuna.create_study(sampler=sampler)
study.optimize(objective, n_trials=30)
# Load the best model.
with open("{}.pickle".format(study.best_trial.number), "rb") as fin:
best_xgb = pickle.load(fin)
#予測値
dval_xgb = xgb.DMatrix(va_x_xgb, feature_names=test_df.columns)
pred = best_xgb.predict(dval_xgb)
preds_xgb.append(pred)
dtest_xgb = xgb.DMatrix(t, feature_names=test_df.columns)
pred_test = best_xgb.predict(dtest_xgb)
preds_test_xgb.append(pred_test)
va_idxes_xgb.append(va_idx)
# バリデーションデータに対する予測値を連結し、その後元の順序に並べ直す
va_idxes_xgb = np.concatenate(va_idxes_xgb)
preds_xgb = np.concatenate(preds_xgb, axis=0)
order = np.argsort(va_idxes_xgb)
pred_train_xgb_1 = preds_xgb[order]
# テストデータに対する予測値の平均をとる
preds_test_xgb_1 = np.mean(preds_test_xgb, axis=0)
GBDTの残り2つのモデルは、max_depthを5,8に変えて作成しデータを作成していきます。
(max_depth以外は基本同じなので割愛します)
参考までに、深さが2,5,8でそれぞれのスコアは、0.7775, 0.7727, 0.7703となり、深さが増えるほどスコアが下がっていました。
■ 1層目のモデル作成|ランダムフォレスト
つづいて、ランダムフォレストでモデル作成、予測値の作成をします。
ランダムフォレストのハイパーパラメータについては、以下記事を参考にしました。
実装は以下になります。
# model2-1: ランダムフォレストでoptunaでの調整をもとにモデルを作成し、クロスバリデーションで学習・予測を行い、予測値を得る
# max_depth:2
# Optunaでハイパーパラメータの調整
def objective(trial):
#ハイパーパラメータの設定
bootstrap = trial.suggest_categorical('bootstrap', ['False', 'True'])
min_samples_split = trial.suggest_uniform('min_samples_split', 0.1, 1.0)
min_samples_leaf = trial.suggest_int('min_samples_leaf', 1, 20)
n_estimators = trial.suggest_int('n_estimators', 5, 20)
max_depth = 2
max_features = trial.suggest_int('max_features', 10,20)
criterion = trial.suggest_categorical('criterion', ['gini', 'entropy'])
#モデルの構築と訓練
model_rdf = RandomForestClassifier(
bootstrap = bootstrap,
min_samples_split = min_samples_split,
min_samples_leaf = min_samples_leaf,
n_estimators = n_estimators,
max_depth = max_depth,
criterion = criterion,
random_state = 0
)
model_rdf.fit(X_train2, y_train2)
#Save a trained model to a file.
with open("{}.pickle".format(trial.number), "wb") as fout:
pickle.dump(model_rdf, fout)
#モデルの評価
pred_rdf = model_rdf.predict(X_val2)
ac_score = accuracy_score(y_val2, pred_rdf)
return ac_score
# 予測値・インデックスの保存用リスト
preds_rf = []
preds_test_rf = []
va_idxes_rf = []
kf_rf = KFold(n_splits=5, shuffle=True, random_state=71)
# クロスバリデーションで学習・予測を行い、予測値とインデックスを保存する
for i, (tr_idx, va_idx) in enumerate(kf_rf.split(X)):
tr_x_rf, va_x_rf = X[tr_idx], X[va_idx]
tr_y_rf, va_y_rf = y[tr_idx], y[va_idx]
# 訓練データのバリデーションデータの分割
X_train2, X_val2, y_train2, y_val2 = train_test_split(tr_x_rf, tr_y_rf, test_size=0.2, random_state=0)
# ハイパーパラメータの最適化
sampler = optuna.samplers.TPESampler(seed=0)
study = optuna.create_study(sampler=sampler, direction='maximize')
study.optimize(objective, n_trials=50)
# Load the best model.
with open("{}.pickle".format(study.best_trial.number), "rb") as fin:
model_rdf_best = pickle.load(fin)
#予測値
pred_rf = model_rdf_best.predict_proba(va_x_rf)[:,1]
preds_rf.append(pred_rf)
pred_rf_test = model_rdf_best.predict_proba(t)[:,1]
preds_test_rf.append(pred_rf_test)
va_idxes_rf.append(va_idx)
# バリデーションデータに対する予測値を連結し、その後元の順序に並べ直す
va_idxes_rf = np.concatenate(va_idxes_rf)
preds_rf = np.concatenate(preds_rf, axis=0)
order = np.argsort(va_idxes_rf)
pred_train_rf_1 = preds_rf[order]
# テストデータに対する予測値の平均をとる
preds_test_rf_1 = np.mean(preds_test_rf, axis=0)
ランダムフォレストの残りのモデルは、max_depthを8に変えて作成しデータを作成していきます。
(max_depth以外は基本同じなので、こちらも割愛します)
参考までに、深さが2, 8でそれぞれのスコアは、0.7822, 0.7775となり、ランダムフォレストも深さが増えるとスコアが下がっていました。
■ 1層目のモデル作成|ニューラルネットワーク
つづいてニューラルネットワークでモデル作成、予測値の作成をします。
個人的には、Pytorchで交差検証をする際のsubsetの扱いに苦戦しまして以下記事が参考になりました。
Epoch数とミニバッチサイズについて以下記事が分かりやすかったのであわせてご紹介いたします。
▶PyTorchでクロスバリデーション(Subsetの使い方)
▶Epoch数とミニバッチサイズの解説と、変化させた時の精度の変化
少し長いですが実装は以下になります。
# model3: optunaでの調整をもとにニューラルネットワークでモデルを作成し、クロスバリデーションで学習・予測を行い、予測値を得るモデル構築
# tensorに変換
X_t = torch.tensor(X, dtype=torch.float32)
y_t = torch.tensor(y, dtype=torch.int64)
# データセット結合
dataset_t = torch.utils.data.TensorDataset(X_t, y_t)
class Net(pl.LightningModule):
def __init__(self, n_layers=1, n_mid=10, lr=0.01):
super().__init__()
self.n_layers = n_layers
self.n_mid = n_mid
self.lr = lr
self.layers = nn.Sequential()
for n in range(self.n_layers):
if n == 0:
self.layers.add_module(f'fc{n+1}', nn.Linear(37, self.n_mid))
else:
self.layers.add_module(f'fc{n+1}', nn.Linear(self.n_mid, self.n_mid))
self.layers.add_module(f'act{n+1}', nn.ReLU())
self.layers.add_module(f'bn{n+1}', nn.BatchNorm1d(self.n_mid))
# 最後の層
self.layers.add_module(f'fc{self.n_layers+1}', nn.Linear(self.n_mid, 2))
def forward(self, x):
h = self.layers(x)
return h
def training_step(self, batch, batch_idx):
x, t = batch
y = self(x)
loss = F.cross_entropy(y, t)
self.log('train_loss', loss, on_step=False, on_epoch=True, prog_bar=True)
return loss
def validation_step(self, batch, batch_idx):
x, t = batch
y = self(x)
loss = F.cross_entropy(y, t)
self.log('val_loss', loss, on_step=False, on_epoch=True, prog_bar=True)
return loss
def test_steps(self, batch, batch_idx):
x, t = batch
y = self(x)
loss = F.cross_entropy(y, t)
self.log('test_loss', loss, on_step=False, on_epoch=True)
return loss
def configure_optimizers(self):
optimizer = torch.optim.SGD(self.parameters(), lr=self.lr)
return optimizer
# Optunaでハイパーパラメータの調整
def objective(trial):
#ハイパーパラメータの候補領域(学習係数、中間層のノード数)
n_layers = trial.suggest_int('n_layers', 2, 3)
lr = trial.suggest_loguniform('lr', 1e-3, 1e-2)
n_mid = trial.suggest_int('n_mid', 80, 100)
#目的関数: 検証データに対する正解率(accuracy)
pl.seed_everything(0)
net = Net(n_layers=n_layers, n_mid=n_mid, lr=lr)
#determinstic : 再現性の担保、seed_everythingと一緒に使う
#CPUを使用する場合は、gpus=Noneとする
trainer = pl.Trainer(max_epochs=100, gpus=1, deterministic=True)
trainer.fit(net, train_loader, val_loader)
#Save a trained model to a file.
with open("{}.pickle".format(trial.number), "wb") as fout:
pickle.dump(net, fout)
return trainer.callback_metrics['val_loss']
# 予測値・インデックスの保存用リスト
preds_nn = []
preds_test_nn = []
va_idxes_nn = []
kf_nn = KFold(n_splits=4, shuffle=True, random_state=71)
# K-分割交差検証の実行部分
for train_index, val_index in kf_nn.split(X_t, y_t):
# データの分割
batch_size = 64
train_data = torch.utils.data.dataset.Subset(dataset_t, train_index)
#train_dataの分割
n_train = int(len(train_data)*0.8)
n_val = len(train_data) - n_train
pl.seed_everything(0) #乱数のシードを固定
#train_dataの分割
train, val = torch.utils.data.random_split(train_data, [n_train, n_val])
train_loader = torch.utils.data.DataLoader(train, batch_size, shuffle=True, drop_last=True)
val_loader = torch.utils.data.DataLoader(val, batch_size, shuffle=True)
# ハイパーパラメータの最適化
sampler = optuna.samplers.TPESampler(seed=0)
study = optuna.create_study(sampler=sampler)
study.optimize(objective, n_trials=20)
# Load the best model.
with open("{}.pickle".format(study.best_trial.number), "rb") as fin:
best_net_nn = pickle.load(fin)
#予測値val
X_t_val = X_t[val_index]
yosoku_val = best_net_nn(X_t_val)
nn_val = F.softmax(yosoku_val)
#予測値test
t_t = torch.tensor(t, dtype=torch.float32)
yosoku_test = best_net_nn(t_t)
nn_test = F.softmax(yosoku_test)
#tensorからnumpyに変換し、生存の予測値のみ取り出す
nn_val = nn_val.to('cpu').detach().numpy().copy()
nn_val = nn_val[:,1]
nn_test = nn_test.to('cpu').detach().numpy().copy()
nn_test = nn_test[:,1]
#作成データの追加
preds_nn.append(nn_val)
preds_test_nn.append(nn_test)
va_idxes_nn.append(val_index)
# バリデーションデータに対する予測値を連結し、その後元の順序に並べ直す
va_idxes_nn = np.concatenate(va_idxes_nn)
preds_nn = np.concatenate(preds_nn, axis=0)
order = np.argsort(va_idxes_nn)
pred_train_nn = preds_nn[order]
# テストデータに対する予測値の平均をとる
preds_test_nn = np.mean(preds_test_nn, axis=0)
参考までに、ニューラルネットワークのスコアは0.7607となりました。
■ 1層目のモデル作成|ロジスティク回帰
1層目の最後は、ロジスティク回帰で予測値を作成します。
ロジスティク回帰のハイパーパラメータは、以下記事を参考にしました。
# model4: ロジスティク回帰でoptunaでの調整をもとにモデルを作成し、クロスバリデーションで学習・予測を行い、予測値を得る
def objective(trial):
#ハイパーパラーメターの候補
C = trial.suggest_uniform('C', 0.001, 1.0)
intercept_scaling = trial.suggest_uniform('intercept_scaling', 0.001, 1)
tol = trial.suggest_uniform('tol', 0.0000001, 0.0001)
# 目的関数
lr_model = LogisticRegression(
solver='liblinear',
C=C,
intercept_scaling=intercept_scaling,
tol=tol,
max_iter=200000,
random_state=0
)
lr_model.fit(X_train2,y_train2)
va_pred = lr_model.predict(X_val2)
score = log_loss(y_val2,va_pred)
#Save a trained model to a file.
with open("{}.pickle".format(trial.number), "wb") as fout:
pickle.dump(lr_model, fout)
return score
# 予測値・インデックスの保存用リスト
preds_lr = []
preds_test_lr = []
va_idxes_lr = []
kf_lr = KFold(n_splits=5, shuffle=True, random_state=71)
# クロスバリデーションで学習・予測を行い、予測値とインデックスを保存する
for i, (tr_idx, va_idx) in enumerate(kf_lr.split(X)):
tr_x_lr, va_x_lr = X[tr_idx], X[va_idx]
tr_y_lr, va_y_lr = y[tr_idx], y[va_idx]
# 訓練データのバリデーションデータの分割
X_train2, X_val2, y_train2, y_val2 = train_test_split(tr_x_lr, tr_y_lr, test_size=0.2, random_state=0)
# ハイパーパラメータの最適化
sampler = optuna.samplers.TPESampler(seed=0)
study = optuna.create_study(sampler=sampler)
study.optimize(objective, n_trials=50)
# Load the best model.
with open("{}.pickle".format(study.best_trial.number), "rb") as fin:
model_lr_best = pickle.load(fin)
#予測値
pred_lr = model_lr_best.predict_proba(va_x_lr)[:,1]
preds_lr.append(pred_lr)
pred_lr_test = model_lr_best.predict_proba(t)[:,1]
preds_test_lr.append(pred_lr_test)
va_idxes_lr.append(va_idx)
# バリデーションデータに対する予測値を連結し、その後元の順序に並べ直す
va_idxes_lr = np.concatenate(va_idxes_lr)
preds_lr = np.concatenate(preds_lr, axis=0)
order = np.argsort(va_idxes_lr)
pred_train_lr = preds_lr[order]
# テストデータに対する予測値の平均をとる
preds_test_lr = np.mean(preds_test_lr, axis=0)# model4: ロジスティク回帰でoptunaでの調整をもとにモデルを作成し、クロスバリデーションで学習・予測を行い、予測値を得る
def objective(trial):
#ハイパーパラーメターの候補
C = trial.suggest_uniform('C', 0.001, 1.0)
intercept_scaling = trial.suggest_uniform('intercept_scaling', 0.001, 1)
tol = trial.suggest_uniform('tol', 0.0000001, 0.0001)
# 目的関数
lr_model = LogisticRegression(
solver='liblinear',
C=C,
intercept_scaling=intercept_scaling,
tol=tol,
max_iter=200000,
random_state=0
)
lr_model.fit(X_train2,y_train2)
va_pred = lr_model.predict(X_val2)
score = log_loss(y_val2,va_pred)
#Save a trained model to a file.
with open("{}.pickle".format(trial.number), "wb") as fout:
pickle.dump(lr_model, fout)
return score
# 予測値・インデックスの保存用リスト
preds_lr = []
preds_test_lr = []
va_idxes_lr = []
kf_lr = KFold(n_splits=5, shuffle=True, random_state=71)
# クロスバリデーションで学習・予測を行い、予測値とインデックスを保存する
for i, (tr_idx, va_idx) in enumerate(kf_lr.split(X)):
tr_x_lr, va_x_lr = X[tr_idx], X[va_idx]
tr_y_lr, va_y_lr = y[tr_idx], y[va_idx]
# 訓練データのバリデーションデータの分割
X_train2, X_val2, y_train2, y_val2 = train_test_split(tr_x_lr, tr_y_lr, test_size=0.2, random_state=0)
# ハイパーパラメータの最適化
sampler = optuna.samplers.TPESampler(seed=0)
study = optuna.create_study(sampler=sampler)
study.optimize(objective, n_trials=50)
# Load the best model.
with open("{}.pickle".format(study.best_trial.number), "rb") as fin:
model_lr_best = pickle.load(fin)
#予測値
pred_lr = model_lr_best.predict_proba(va_x_lr)[:,1]
preds_lr.append(pred_lr)
pred_lr_test = model_lr_best.predict_proba(t)[:,1]
preds_test_lr.append(pred_lr_test)
va_idxes_lr.append(va_idx)
# バリデーションデータに対する予測値を連結し、その後元の順序に並べ直す
va_idxes_lr = np.concatenate(va_idxes_lr)
preds_lr = np.concatenate(preds_lr, axis=0)
order = np.argsort(va_idxes_lr)
pred_train_lr = preds_lr[order]
# テストデータに対する予測値の平均をとる
preds_test_lr = np.mean(preds_test_lr, axis=0)
参考までにロジスティク回帰のスコアは0.7822でした。
スタッキングに含めるモデルの選択
相関係数が0.95以下かつ、2つの母集団の確率分布が異なるかを検定するコルモゴロフ-スミルノフ検定統計量が0.05以上のモデルを選んでいきます。
ます1層目の予測値の相関係数を確認します。
# 1層目の予測値をまとめる
st_pred_train = pd.DataFrame(
{'GBDT_1': pred_train_xgb_1.ravel(),
'GBDT_2': pred_train_xgb_2.ravel(),
'GBDT_3': pred_train_xgb_3.ravel(),
'RF_1': pred_train_rf_1.ravel(),
'RF_2': pred_train_rf_2.ravel(),
'NN': pred_train_nn.ravel(),
'LR': pred_train_lr.ravel(),
})
print('st_pred_train.shape : ', st_pred_train.shape)
# 相関係数をみる
corr_1 = st_pred_train.corr()
corr_1[corr_1<0.95]
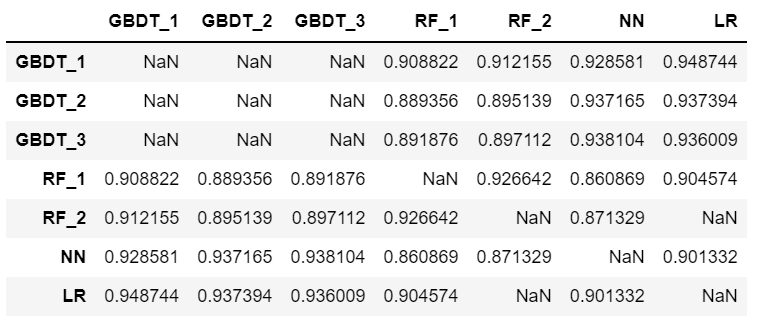
相関係数とスコアを考慮して、
GBDT(浅いもの)、ランダムフォレスト(浅いもの)、ニューラルネットワーク、ロジスティク回帰の4つのモデルが残りました。
続いて、コルモゴロフ-スミルノフ検定統計量を見ていきます。
# IN
ks_2samp(st_pred_train['GBDT_1'],st_pred_train['RF_1'])
# OUT
KstestResult(statistic=0.4657687991021324, pvalue=1.1843502200279904e-87)
# IN
ks_2samp(st_pred_train['GBDT_1'],st_pred_train['NN'])
# OUT
KstestResult(statistic=0.12457912457912458, pvalue=1.919759289471497e-06)
# IN
ks_2samp(st_pred_train['GBDT_1'],st_pred_train['LR'])
# OUT
KstestResult(statistic=0.143658810325477, pvalue=1.958435434828125e-08)
# IN
ks_2samp(st_pred_train['RF_1'],st_pred_train['NN'])
# OUT
KstestResult(statistic=0.3782267115600449, pvalue=3.7722856358158184e-57)
# IN
ks_2samp(st_pred_train['RF_1'],st_pred_train['LR'])
# OUT
KstestResult(statistic=0.40852974186307517, pvalue=6.771154620933685e-67)
# IN
ks_2samp(st_pred_train['NN'],st_pred_train['LR'])
# OUT
KstestResult(statistic=0.12121212121212122, pvalue=4.026512278533246e-06)
いずれも統計量が0.05以上なので、4つのモデルのデータをもとに2層目のモデルを作成していきます。
2層目のモデル作成
1層目で作成したデータを学習・予測用に変形します。
# 1層目で作成したデータを縦持ちに変形
# 訓練データ
pred_train_xgb_st = pred_train_xgb_1.reshape(-1,1)
pred_train_rf_st = pred_train_rf_1.reshape(-1,1)
pred_train_nn_st = pred_train_nn.reshape(-1,1)
pred_train_lr_st = pred_train_lr.reshape(-1,1)
# テストデータ
preds_test_xgb_st = preds_test_xgb_1.reshape(-1,1)
preds_test_rf_st = preds_test_xgb_1.reshape(-1,1)
preds_test_nn_st = preds_test_nn.reshape(-1,1)
preds_test_lr_st = preds_test_lr.reshape(-1,1)
# データ結合
st_train = np.concatenate((pred_train_xgb_st, pred_train_rf_st,pred_train_nn_st,pred_train_lr_st), axis=1)
st_test = np.concatenate((preds_test_xgb_st, preds_test_rf_st,preds_test_nn_st,preds_test_lr_st), axis=1)
2層目は、ロジスティク回帰でモデル作成し予測データを得ます。
# 2層目: ロジスティク回帰でoptunaでの調整をもとにモデルを作成、予測値を得る
# 訓練データのバリデーションデータの分割
X_train_st, X_val_st, y_train_st, y_val_st = train_test_split(st_train, y, test_size=0.20, random_state=0)
def objective(trial):
#ハイパーパラーメターの候補
penalty = trial.suggest_categorical('penalty', ['l1', 'l2'])
C = trial.suggest_uniform('C', 0.001, 1000.0)
intercept_scaling = trial.suggest_uniform('intercept_scaling', 0.001, 1)
tol = trial.suggest_uniform('tol', 0.0000001, 0.0001)
# 目的関数
lr_model_st = LogisticRegression(
penalty=penalty,
solver='liblinear',
C=C,
intercept_scaling=intercept_scaling,
tol=tol,
max_iter=200000,
random_state=0
)
lr_model_st.fit(X_train_st,y_train_st)
va_pred = lr_model_st.predict(X_val_st)
score = log_loss(y_val_st,va_pred)
#Save a trained model to a file.
with open("{}.pickle".format(trial.number), "wb") as fout:
pickle.dump(lr_model_st, fout)
return score
# Optunaオブジェクトを作成
sampler = optuna.samplers.TPESampler(seed=0)
study = optuna.create_study(sampler=sampler)
# Optunaでパラメータ探索
study.optimize(objective, n_trials=100)
# Load the best model
with open("{}.pickle".format(study.best_trial.number), "rb") as fin:
best_la_st = pickle.load(fin)
# 予測
pred_submit_LR = best_la_st.predict_proba(st_test)
# 中身の確認
np.set_printoptions(suppress=True)
pred_submit_LR[:20]
参考までに、予測値を提出すると0.7918というスコアが得られました。
さいごに
記事の中でもご紹介をしてきましたが、多くの技術系記事が公開されているおかげで実装することができました。私自身も学んだことは出来る限り発信して、少しでもほかのどなたかのお役に立てば嬉しいです。