Louvain Clustering
Louvain法はグラフクラスタリングの一種であり、ある程度の大きさのグラフを高速に分割できることから広く用いられてきた。生命科学分野ではsingle-cell seqなどの高次元データの可視化にUMAP、クラスタリングにLouvain ClusteringやLeiden Clusteringなどが用いられてきた。
グラフクラスタリングの変遷については以下に詳しい。
塩川 浩昭. "⼤規模グラフデータ分析⼊⾨" 第8回「学際計算科学による新たな知の発⾒・統合・創出」シンポジウム. 筑波⼤学 計算科学研究センター. 2016.
現在広く用いられているグラフクラスタリングの基礎となったLouvain Clusteringについてゼロから作り、理解を目指す。
Modularity
fraction of edges that fall within communities, minus the expected value of the same quantity if edges fall at random without regard for the community structure
モジュラリティはクラスター(以下コミュニティ)への分割の意義付けとして導入された関数で、「コミュニティ内のエッジ数」から「ランダムさを仮定した場合のコミュニティ内のエッジ数の期待値」を引いた値を、全体のエッジ数で割った値として定義される。
Louvainの論文にはアルゴリズムやpseudo-codeなど詳述されていないが、以下のLeidenクラスタリングの文献はまとまっていて読みやすい。
また、和文は以下に詳しい。
紫藤佑介, et al. "モジュラリティを基準とした関係データに対する特徴選択." 人工知能学会研究会資料 人工知能基本問題研究会 103 回. 一般社団法人 人工知能学会, 2017.
コミュニティから考えた時のModularity(Newmanらの表現)
単純無向グラフで、エッジは単に二つのノードが接続しているかないかを表している様な場合を考える。ここで断りなく割合というとき、ネットワーク内のエッジの総和に対した割合を意味するとする。
ネットワーク内のコミュニティを添え字$r$、$s$を用いて表すとき、全体のエッジの総和に対するコミュニティ$r$とコミュニティ$s$との間に張られたエッジの総和の割合を$f_{rs}$とする。このとき、$f_{rr}$はコミュニティ$r$内に張られたエッジの総和の割合である。
${f_{rs}}$行列の行(もしくは列)の総和、$a_r = \sum_s{f_{rs}}$は、ネットワーク全体からコミュニティ$r$内のノードに対して張られたエッジの総和の割合であり、コミュニティ$r$から見た手の期待値である。もしコミュニティとエッジが独立であれば、$f_{rs} = a_r a_s$となるはずである。同様に、$f_{rr} = a_r^2$となる。ここでモジュラリティ$Q$を
Q = \sum_r{f_{rr}-a_r^2}
とする。
ノード、隣接行列から考えた時のModularity(Blondelらの表現)
隣接行列を用いた定義であり、より直截的であるが、ループの扱いの上で次数を用いた実装と乖離があることに留意する。ちなみにLouvainは著者らの所属する大学、ベルギーの都市の名前である。
元の文献にはないが、あるコミュニティ$r$に属するノードの集合を$v_r$とする。
ノードの次数$k_i$を以下のように定める。
k_i = \sum_j{A_{ij}}
また隣接行列${A_{ij}}$の総和から$M$を以下のように定める。
M = \frac{1}{2}\sum_{i,j}{A_{ij}}
特に、無向グラフの接続しているエッジの重みを1、そうでない場合を0とした隣接行列においては$M$はエッジの総数に等しいことに留意する。
あるノード$i$が所属するコミュニティを$c(i)$とするとき
\delta(c(i),c(j)) =
\begin{cases}
1 & ( c(i) = c(j) ) \\
0 & ( otherwise )
\end{cases}
なる$\delta(c(i),c(j))$を定める。このとき$f_{rs} = \sum_{i \in v_r, j \in v_s}{\frac{A_{ij}}{2M}}$であるから、特にあるコミュニティ内のエッジのみに着目したときは$\delta$を用いて
\begin{align}
\sum_r{f_{rr}} &= \sum_r{\sum_{i \in v_r, j \in v_r}{\frac{A_{ij}}{2M}}}\\
&= \sum_{i,j}{\frac{A_{ij}}{2M}\delta(c(i),c(j))}
\end{align}
と表せる。添え字の範囲がなくなった代わりに、コミュニティ内に張られるエッジに対してクロネッカ―のデルタで対応している。一方でエッジの割合の期待値については、$k_i = \sum_j{A_{ij}}$を用いて
\begin{align}
a_r &= \sum_s{f_{rs}} = \sum_s{\sum_{i \in v_r, j \in v_s}{\frac{A_{ij}}{2M}}} \\
&= \sum_{i \in v_r}{\sum_{j}{\frac{A_{ij}}{2M}}} \\
&= \sum_{i \in v_r}{\frac{k_i}{2M}}\\
\end{align}
従って、コミュニティ内のエッジの総和の割合の期待値をすべてのコミュニティについて総和をとったものは
\begin{align}
\sum_r{a_r^2} &= \sum_r{\left(\sum_{i \in v_r}{\frac{k_i}{2M}}\right)^2}\\
&= \sum_r{\sum_{i \in v_r, j \in v_r}{\frac{k_i k_j}{(2M)^2}}}\\
&=\sum_{i,j}{\frac{k_i k_j}{(2M)^2}\delta(c(i),c(j))}
\end{align}
以上よりモジュラリティ$Q$は
\begin{align}
Q &= \sum_{i,j}{\left(\frac{A_{ij}}{2M} - \frac{k_i k_j}{(2M)^2}\right)\delta(c(i),c(j))}\\
& = \frac{1}{2M}\sum_{i,j}{\left(A_{ij}- \frac{k_i k_j}{2M}\right)\delta(c(i),c(j))}
\end{align}
前準備
Louvain法はLocal moveとAggregationの2段階を繰り返し、グラフを単純化していく。Local moveではノードをランダムに選び、周辺のコミュニティに動かした場合の中で最善のモジュラリティとなる場所へノードを動かす。最終的にグラフの中のどのノードを動かしてもモジュラリティが改善しなくなった時に、Aggregationではコミュニティを一つのノードへとまとめ、グラフを更新する。
Local moveとAggregationの2段階を繰り返し、最終的に(Aggregationした)どのノードも動かせなくなった時のノードが分割そのものになる。このアルゴリズムでは、Local moveの段階ではグラフ全体のモジュラリティを計算する必要がなく、ノードとノードを追加するコミュニティごとに変化量だけを求めればよい。
Leidenクラスタリングの論文で指摘されている通り、これはLouvainクラスタリングが保障する性能を正確にのべている。
In fact, although it may seem that the Louvain algorithm does a good job at finding high quality partitions, in its standard form the algorithm provides only one guarantee: the algorithm yields partitions for which it is guaranteed that no communities can be merged. In other words, communities are guaranteed to be well separated.
このアルゴリズムは最終的に得られたどのコミュニティを統合してもモジュラリティが改善しないことは確かだが、そのコミュニティへの分割のもととなったLocal moveが最善でない可能性がある。Leiden法ではこの問題点を指摘し、改善を目指している。
モジュラリティの変化量
ノードの除去
ノード$i$およびノード$i$が所属するコミュニティ$c(i)$を考える。コミュニティからノード$i$を孤立させたときのモジュラリティの変化$\Delta Q_-$は、コミュニティでの変化量$\Delta Q_{{c(i)}-}$と孤立ノードでの変化量$\Delta Q_{isolated}$の和になる。後者の孤立ノードについては最終的に他コミュニティへの追加によって相殺されることから無視してよい。周辺コミュニティにとっては接続の本数は変わらないため無視してよい。従って所属していたコミュニティでの変化量を考えると
\begin{align}
\Delta Q_{{c_i}-}
&= \{\Delta f_{{c(i)}{c(i)}}\} - \{(a_{c(i)} + \Delta a_{c(i)})^2 - a_{c(i)}^2\}\\
&= \Delta f_{{c(i)}{c(i)}} - \{2a_{c(i)}\Delta a_{c(i)} + (\Delta a_{c(i)})^2\}
\end{align}
このうち、$\Delta f_{{c(i)}{c(i)}}$はコミュニティ$c(i)$内でノード$i$とその他のノードの間に張られるエッジが減少する分だから、
\Delta f_{{c_i}{c_i}} = -\frac{1}{2M}\sum_{j \in {c(i)}}{A_{ij}}
また$\Delta a_{c(i)}$はコミュニティ$c(i)$から伸びる手のうちノード$i$の寄与分だから
\Delta a_{c(i)} = -\frac{1}{2M}k_i
従って、
\begin{align}
\Delta Q_{{c(i)}-} &= -\frac{1}{2M}\sum_{j \in {c(i)}}{A_{ij}} + 2a_{c(i)}\frac{1}{2m}k_i - \left(\frac{1}{2M}k_i\right)^2\\
& = \frac{1}{2M}\left(-\sum_{j \in {c(i)}}{A_{ij}} + 2a_{c(i)} k_i - \frac{k_i^2}{2M}\right)
\end{align}
ノードの追加
孤立したノード$i$をあるコミュニティ$c$に追加したときのモジュラリティの変化量$Q_+$は先と同様に
\begin{align}
\Delta Q_{{c}+}
&= \Delta f_{{c}{c}} - \{2a_{c}\Delta a_{c} + (\Delta a_{c})^2\}
\end{align}
このうち、$\Delta f_{{c}{c}}$はコミュニティ$c$内とノード$i$との間に張られるエッジが増加する分であるから、
\Delta f_{{c}{c}} = \frac{1}{2M}\sum_{j \in {c}}{A_{ij}}
また$\Delta a_{c}$はコミュニティ$c$から伸びる手のうちノード$i$の寄与分だから
\Delta a_{c_i} = \frac{1}{2M}k_i
従って、
\begin{align}
\Delta Q_{{c}+} &= \frac{1}{2M}\sum_{j \in {c}}{A_{ij}} - 2a_{c}\frac{1}{2M}k_i - \left(\frac{1}{2M}k_i\right)^2\\
& = \frac{1}{2M}\left(\sum_{j \in {c}}{A_{ij}} - 2a_{c} k_i - \frac{k_i^2}{2M}\right)
\end{align}
ノードをコミュニティからコミュニティへ移動させた場合のモジュラリティの変化
$\Delta Q_{{c(i)}-}$及び$\Delta Q_{{c}+}$を考えるとき、ノードの次数やネットワークのサイズは固定だが、$a_{c(i)}$、$a_c$はノードの移動の前に求めることに留意する。
\Delta Q_{{c(i)}-} = \frac{1}{2M}\left(-\sum_{j \in {c(i)}}{A_{ij}} + 2a_{c(i)} k_i - \frac{k_i^2}{2M}\right)
及び
\Delta Q_{{c}+} = \frac{1}{2M}\left(\sum_{j \in {c}}{A_{ij}} - 2a_{c} k_i - \frac{k_i^2}{2M}\right)
より、評価したい変化量$\Delta Q = \Delta Q_{{c(i)}-} + \Delta Q_{{c}+}$は
\Delta Q =
\frac{1}{2M}\left(-\sum_{j \in {c(i)}}{A_{ij}} + 2a_{c(i)} k_i - 2\frac{k_i^2}{2M} + \sum_{j \in {c}}{A_{ij}} - 2a_c k_i \right)
評価の都合から考えて、係数と項を整理した評価関数$q_1(i)$、$q_2(c,i)$
q_1(i) = -\frac{1}{2}\sum_{j \in {c(i)}}{A_{ij}} + a_{c(i)} k_i - \frac{k_i^2}{2M}\\
q_2(i) = \frac{1}{2}\sum_{j \in {c}}{A_{ij}} - a_{c} k_i\\
\Delta Q = \frac{1}{2M}2(q_1(i) + q_2(i))
をそれぞれノード$i$を除去する前、除去した後に計算し、その和が最も最大となるコミュニティ$c$をランダムに探索すればよい。
グラフ操作と隣接行列の操作の関係
基本的にはエッジの重みの和をとること以外は行わない。
karate_clubの部分グラフを具体例とした隣接行列と次数の関係の確認
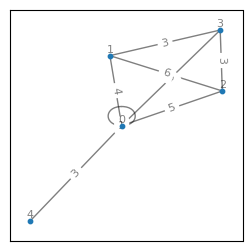
例としてkarate_club_graph()の部分グラフを扱う。このグラフにはループがないため、ノード0に重み1のループを加えグラフを考える。
import networkx as nx
import matplotlib.pyplot as plt
def show_graph(G):
fig, ax = plt.subplots()
fig.set_size_inches(3,3)
pos = nx.spring_layout(G)
nx.draw_networkx_nodes(G, pos, node_size = 10, ax = ax)
nx.draw_networkx_edges(G, pos, alpha=0.5, ax = ax)
nx.draw_networkx_labels(
G,
pos,
labels = {i:f'{i}\n' for i, v in G.nodes.items()},
font_size= 8,
alpha=0.5,
ax = ax
)
nx.draw_networkx_edge_labels(
G,
pos,
edge_labels={i:v['weight'] for i, v in G.edges.items()},
font_size= 8,
alpha=0.5,
ax = ax)
plt.show()
print(nx.adjacency_matrix(G).toarray())
G = nx.karate_club_graph()
g = nx.subgraph(G, [i for i in range(5)]).copy()
g.add_edge(0, 0, weight=1)
show_graph(g)
[[1 4 5 3 3]
[4 0 6 3 0]
[5 6 0 3 0]
[3 3 3 0 0]
[3 0 0 0 0]]
エッジの総和(サイズ)
エッジの総和と隣接行列の総和は異なり、また二倍の関係にもない。ループがない場合は二倍の関係にある。
g.size(weight='weight'), nx.adjacency_matrix(g).sum()
(28.0, 55)
これからわかるように、エッジ集合$E$のエッジ$e \in E$の重みの総和は、該当する隣接行列の三角部分の総和に等しい。
\sum_{e \in E}w(e) = \sum_i{\sum_{j \geq i}A_{ij}}
次数、次数の総和
次数は定義よりループについては2倍にして足す。次数の総和はエッジの総和の二倍に等しく、握手定理と呼ばれる。
sum([g.degree(node, weight='weight') for node in g])
56
以上からわかる通り、次数を用いて作業する以上、隣接行列の総和の操作はループ部分で破綻することになる。以下taynaudの実装に倣い次数をベースに考え、隣接行列から離れることを目指す。
実装にむけて
参考
論文にも解説記事にもアルゴリズムについての詳細がないため、コードから読み解いていく。使用例からはnetworkxのGraphオブジェクトを受け取るbest_partition()があるが、これは実際にはgenerate_dendrogram()のラッパーに過ぎない。
ここでいうdendrogramはdictのlistであり、階層ごとに割り当てられたnode:communityがdictとして記録されている。最終的にこれを順に処理して各nodeが最終的にどのcommunityに属するかを返すのがpartition_at_level()であり、整理されたdendrogramがpartitionに相当する。実際にノードを移動させているのは__one_level(graph, status, weight_key, resolution, random_state)である。
より実装に即した定義
今回は改めて次数を基準に定義を整理する。無向重み付きグラフ$G$がエッジ集号$E_G$及びノード集合$V_G$、もしくは隣接行列$A$で定義されているとする。グラフ$G$で定義されるノード$i$の次数は
\begin{align}
k_G(i) &= \sum_j{A_{ij}} + A_{ii}\\
&= \sum_{e \in h_i} {w(e)}
\end{align}
このとき、$w$はそのエッジの重みを返す関数であり、ループである場合は重みの2倍を返す。$h_i$はノード$i$からグラフ$G$に伸びるエッジ集合とする。
またサイズ$M_G$を以下のように定める。
\begin{align}
M_G &= \frac{1}{2}\left(\sum_{i,j}{A_{ij}} + \sum_{i}{A_{ii}}\right)\\
&= \frac{1}{2}\sum_i{k_G(i)}
\end{align}
グラフ$G$がコミュニティ$c$によって相互排他的に網羅的に分割できる時、コミュニティ$c$(部分グラフ)の「次数」を、
\begin{align}
K_G(c) &= \sum_{i \in c,j}{A_{ij}} + \sum_{i \in c}{A_{ii}}\\
&= \sum_{i \in c}\sum_{e \in h_i} {w(e)}\\
&= \sum_{i \in c}k_G(i)
\end{align}
とすると、$2M = \sum_{c \in G}K_G(c)$が成り立つ。これはコミュニティに含まれる全ノードから伸びるエッジの総和(ループは2回分数える)に相当する。
このとき、コミュニティ内部の次数の総和が、コミュニティそのものをグラフとしてみなしたときのサイズの2倍に相当することを考えると、
\begin{align}
\sum_{i \in c, j \in c}{A_{ij}} + \sum_{i \in c}A_{ii}
&= \sum_{i \in c}{k_c(i)}\\
&= 2M_c
\end{align}
コミュニティ内部の次数の総和の割合である$f_{cc}$は
f_{cc} = \frac{M_c}{M_G}
最後に$a_c$について、
a_c = \frac{1}{2M_G}K_G(c)
以上より、隣接行列を用いずに次数によって扱えることが確認できた。
実装
インスタンス変数
初期値として与える変数
| インスタンス変数名 | 内容 |
|---|---|
| weight_key | networkx.classes.graph.Graphのエッジの重みのキー |
Aggregationごと(Graphごと)に更新
| インスタンス変数名 | 内容 |
|---|---|
| node_degrees | ノードの次数 |
| loops | ノードのループ |
| graph | グラフ |
| size | グラフのサイズ |
| dendrogram | レベルごとのpartitionからなるリスト |
Local moveごとに更新
| インスタンス変数名 | 内容 |
|---|---|
| partition | クラスタリング |
| community_degrees | コミュニティの次数 |
| subgraph_sizes | コミュニティのサイズ |
Louvainクラス
import numpy as np
import networkx as nx
ITER_LIMIT_PER_LOCALMOVE = -1
MIN = 0.0000001
def renumber(dictionary):
unique_values = set(dictionary.values())
int_sequence = set(range(len(unique_values)))
if unique_values == int_sequence:
result = dictionary.copy()
else:
renumbering = dict(zip(int_sequence.intersection(unique_values),
int_sequence.intersection(unique_values)))
renumbering.update(dict(zip(unique_values.difference(int_sequence),
int_sequence.difference(unique_values))))
result = {k: renumbering[v] for k, v in dictionary.items()}
return result
class Louvain:
def __init__(self, graph, RandomGenerator = None):
self.weight_key = 'weight'
if RandomGenerator:
self.random_generator = RandomGenerator
else:
self.random_generator = np.random.default_rng()
self._init_with_graph(graph)
self.dendrogram = list()
def _init_with_graph(self, graph):
self.partition = dict([])
self.node_degrees = dict([])
self.community_degrees = dict([])
self.size = None
self.subgraph_sizes = dict([])
self.loops = dict([])
self.graph = graph
weight_key = self.weight_key
self.size = float(graph.size(weight=weight_key))
for community, node in enumerate(graph.nodes()):
self.partition[node] = community
node_degree = float(graph.degree(node, weight=weight_key))
self.community_degrees[community] = node_degree
self.node_degrees[node] = node_degree
# loop
loop_edge = graph.get_edge_data(node, node, default={weight_key: 0.}) # ない場合は重み0のエッジを登録
self.loops[node] = float(loop_edge.get(weight_key))
self.subgraph_sizes[community] = self.loops[node]
def _modularity(self):
m = self.size
result = 0.
for community in set(self.partition.values()):
m_c = self.subgraph_sizes.get(community, 0.)
K_c = self.community_degrees.get(community, 0.)
result += m_c / m - ((K_c / (2. * m)) ** 2)
return result
def _randomize(self, items):
randomized_items = list(items)
self.random_generator.shuffle(randomized_items)
return randomized_items
def _linksum_of_neighcom_dict(self, node, graph):
weight_key = self.weight_key
linksum_dict = {}
for neighbor_node, edge in graph[node].items():
if neighbor_node != node: # ループでさえなければ同じコミュニティだろうが登録
neighbor_community = self.partition[neighbor_node]
linksum_dict[neighbor_community] = linksum_dict.get(neighbor_community, 0) + edge.get(weight_key)
return linksum_dict
def _remove_node(self, node, linksum_dict):
community = self.partition.get(node)
linksum = linksum_dict.get(community, 0.)
self.community_degrees[community] = self.community_degrees.get(community, 0.) - self.node_degrees.get(node, 0.)
self.subgraph_sizes[community] = self.subgraph_sizes.get(community, 0.) - linksum - self.loops.get(node, 0.)
self.partition[node] = -1
def _insert_node(self, node, community, linksum_dict):
linksum = linksum_dict.get(community, 0.)
self.partition[node] = community
self.community_degrees[community] = self.community_degrees.get(community, 0.) + self.node_degrees.get(node, 0.)
self.subgraph_sizes[community] = self.subgraph_sizes.get(community, 0.) + linksum + self.loops.get(node, 0.)
def _delta_q_1(self, node, linksum_dict):
community = self.partition.get(node)
ki = self.node_degrees.get(node, 0.)
ac2m = self.community_degrees.get(community, 0.)
m = self.size
linksum = linksum_dict.get(community, 0.)
result = - linksum + ac2m*ki/(2*m) - ki**2/(2*m)
return result
def _delta_q_2(self, node, linksum_dict, neighboring_community):
ki = self.node_degrees.get(node, 0.)
ac2m = self.community_degrees.get(neighboring_community, 0.)
m = self.size
linksum = linksum_dict.get(neighboring_community, 0.)
result = linksum - ac2m*ki/(2*m)
return result
def _move_nodes(self, graph):
modified = True
nb_pass_done = 0
current_Q = self._modularity()
new_Q = current_Q
while modified and nb_pass_done != ITER_LIMIT_PER_LOCALMOVE:
current_Q = new_Q
modified = False
nb_pass_done += 1
for node in self._randomize(graph.nodes()):
original_community = self.partition.get(node)
linksum_dict = self._linksum_of_neighcom_dict(node, graph) # あるノードからみた周辺コミュニティごとのエッジの和
q1 = self._delta_q_1(node, linksum_dict)
self._remove_node(node, linksum_dict)
best_community = original_community
best_increase = 0
for neighboring_community in self._randomize(linksum_dict.keys()): # 隣接コミュニティをランダムに選択し、
delta_Q = q1 + self._delta_q_2(node, linksum_dict, neighboring_community)
if delta_Q > best_increase:
best_increase = delta_Q
best_community = neighboring_community
self._insert_node(node, best_community, linksum_dict)
if best_community != original_community:
modified = True
new_Q = self._modularity()
if new_Q - current_Q < MIN:
break
def generate_dendrogram(self):
current_graph = self.graph.copy()
partition_list = list()
self._move_nodes(current_graph)
renumberd_partition = renumber(self.partition)
partition_list.append(renumberd_partition)
new_Q = self._modularity()
Q = new_Q
current_graph = self._aggregate_nodes(renumberd_partition, current_graph)
self._init_with_graph(current_graph)
while True:
self._move_nodes(current_graph)
new_Q = self._modularity()
if new_Q - Q < MIN:
break
renumberd_partition = renumber(self.partition)
partition_list.append(renumberd_partition)
Q = new_Q
current_graph = self._aggregate_nodes(renumberd_partition, current_graph)
self._init_with_graph(current_graph)
self.dendrogram = partition_list[:]
def _aggregate_nodes(self, partition, graph):
weight = self.weight_key
aggregated_graph = nx.Graph()
aggregated_graph.add_nodes_from(partition.values())
for node1, node2, datas in graph.edges(data=True):
edge_weight = datas.get(weight, 1)
com1 = partition[node1]
com2 = partition[node2]
w_prec = aggregated_graph.get_edge_data(com1, com2, {weight: 0}).get(weight, 1)
aggregated_graph.add_edge(com1, com2, **{weight: w_prec + edge_weight})
return aggregated_graph
def fit(self):
self.generate_dendrogram()
partition = self.dendrogram[0].copy()
for level in range(1, len(self.dendrogram)):
for node, community in partition.items():
partition[node] = self.dendrogram[level][community]
return partition
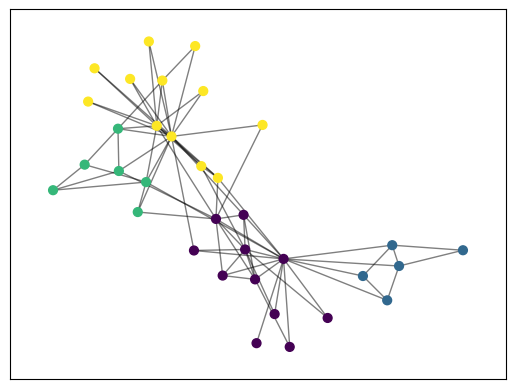
karate_clubの例
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import networkx as nx
G = nx.karate_club_graph()
l = Louvain(G)
partition = l.fit()
pos = nx.spring_layout(G)
cmap = cm.get_cmap('viridis', max(partition.values()) + 1)
fig, ax = plt.subplots()
nx.draw_networkx_nodes(
G,
pos,
partition.keys(),
node_size=40,
cmap=cmap,
node_color=list(partition.values()),
ax = ax
)
nx.draw_networkx_edges(
G,
pos,
alpha=0.5,
ax = ax
)
plt.show()