概要
ソーシャルネット分析に含まれるLink Predictionについて、その精度がトポロジーに依存するだろうことを実験で確認する。
- 実施期間: 2022年3月
- 環境:Ubuntu20.04 LTS
- パケージ:scikit network, networkx
1. パケージ
使用するモデルにはDirected Graphを指定する。
ソーシャルネットは誰が誰をフォローしているだとか、どのサイトがどのサイトのリンクを張っているかだとか、どの論文がどの論文をciteしたか、方向があることが普通。
しかし馴染みのnetworkxや、いろんなアルゴリズムを実装したnetworkitはDirected Graphに対応していないAPIが多すぎて使えないので、ここではscikit networkで評価する。
importするパケージは下記となる。
import numpy as np
import pandas as pd
import powerlaw
import statistics
import networkx as nx
import sknetwork as skn
import matplotlib.pyplot as plt
from IPython.display import SVG
from sknetwork.data import albert_barabasi, erdos_renyi, watts_strogatz
from sknetwork.visualization import svg_graph, svg_digraph, svg_bigraph
from sknetwork.linkpred import PreferentialAttachment, CommonNeighbors, is_edge, whitened_sigmoid
from sklearn import metrics
2. グラフモデル
下記の2つのモデルについて、node数とdegreeを変化させたとき、Link Predictionの精度が変わるか確認する。
| model | note |
|---|---|
| albert barabasi | Barabasiが提唱したPreferencial attatchmentを再現するモデル |
|
|
|
| watts strogatz | ランダムモデルの一種でSmall worldを再現するモデル |
*1) 戻りのAdjacency matrixに自己ループ情報がFalseで入るといった特殊なものだったので評価しないこととした。
## albert barabasi
num_node = 10
num_degree = 3
adjacency = albert_barabasi(n=num_node, degree=num_degree, undirected=True, seed=12)
image = svg_graph(adjacency, display_node_weight=True)
SVG(image)
## watts strogatz
num_node = 10
num_degree = 3
prob = .6
adjacency = watts_strogatz(n=num_node, degree=num_degree, prob=prob, seed=12)
image = svg_graph(adjacency, display_node_weight=True)
SVG(image)
それぞれ下記が描画されるが、グラフにおいて目視で得られる情報はしれているためデバッグ程度の確認に留めること。
albert barabasi model
watts strogatz model
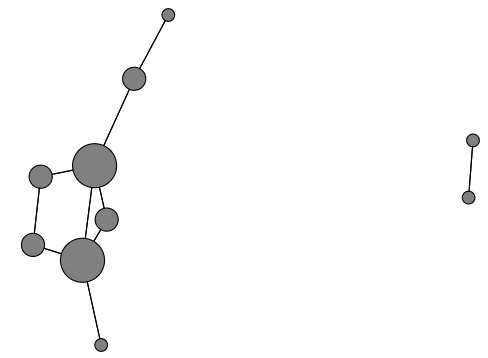
watts strogatz modelは格子状グラフにおいてランダム(Probabiliyは指定)に選択したnodeペアのLinkを、バイパスとなるように張り替える処理が行われる。これによりPathが短くなりSmall Worldに近づく。従いパラメータによっては上図のようにcomponentが2以上となってしまう。今回の実験ではこれが起こらないようにパラメータでごまかしたがLink Predictionを実装するときはStrongly connected componentが1つしかないようにする処理が必要となる。
component数はnetworkxのnx.strongly_connected_components(G)で取得可能
尚、このモデルはSix degrees of separationの説明で使用される。
尚々、映画の共演者ネットワークでこれを体感できる。
3. EDA
node_numを1000として両グラフモデルのMetricsを確認する。
arr = adjacency.indptr
degree_lst = [arr[i+1]-arr[i] for i in range(len(arr)-1)]
degree_arr = np.array(degree_lst)
print(f'total_edges: {np.sum(degree_lst)}')
print(f'max_degree: {np.max(degree_lst)}')
print(f'median_degree: {statistics.median(degree_lst)}')
print('dencity = {:.5f}'.format(sum(adjacency.data)/(num_node*(num_node-1))))
fit = powerlaw.Fit(degree_lst)
print('ganma = {:.5f}'.format(fit.power_law.alpha))
print(f'ganma(min): {fit.power_law.xmin}')
hetero_param = sum(degree_arr**2)/num_node/(sum(degree_arr)/num_node)**2
print('Heterogeneity param = {:.5f}'.format(hetero_param))
degree_lst = sorted(degree_lst, reverse=True)
plt.xscale("log")
plt.xlabel("degree")
plt.yscale("log")
plt.ylabel("number of nodes")
plt.plot(degree_lst)
plt.show()
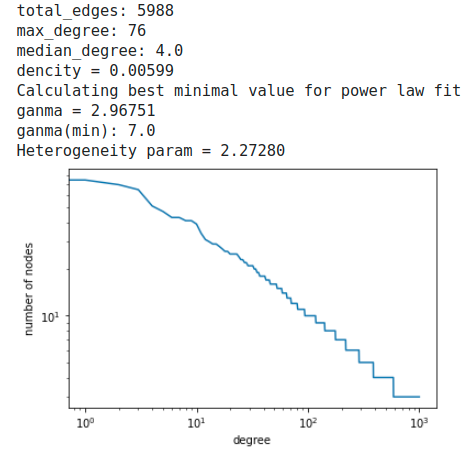
albert barabasi model
watts strogatz model
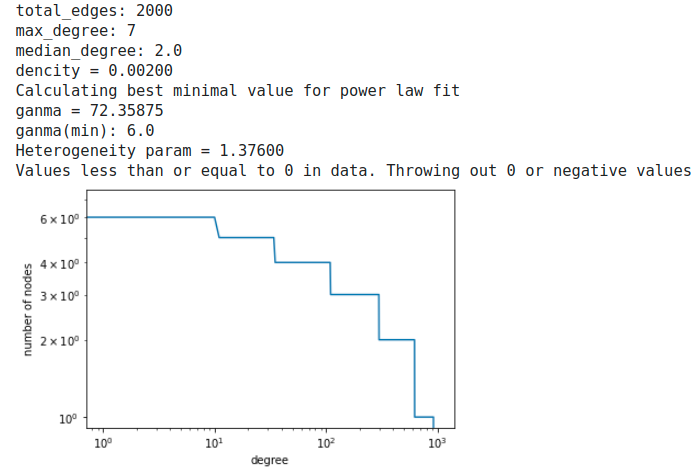
Complicate Graphはalbert barabasi modelのように裾野が長くなり、ganmaが2~3になると言われている。3を超えるとランダムグラフとみなされる。
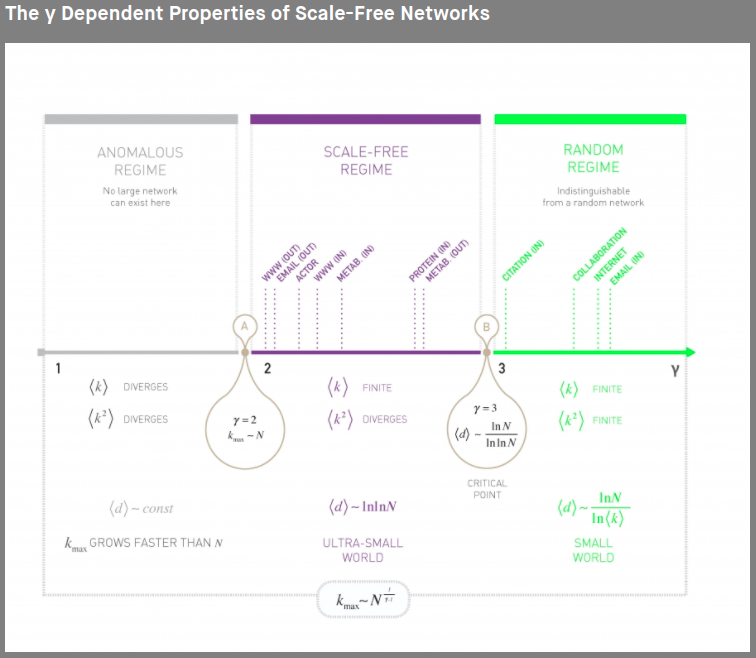
参照:http://networksciencebook.com/chapter/4#degree-exponent
今回のbarabasi modelのganmaは3より小さくDegree distributionの裾野が長く伸び、Hubとなる大きなdegreeをもつnodeが少数あることがこの分布からもわかる。Degree distributionのどこを切り取っても同じdistributionになることからScale-free networkと呼ばれる。
またグラフのheterogeneity parameterも1を超えているため、heterogeneous graphと言える。
一方、watts strogatz modelはganmaが72と非常に大きいくdegreeの分布は比較すると一様になっていて完全なRandom graphとわかる。ただheterogeneity parameterが1を超えているため、これについては別に考察が必要(おいらの勉強不足かも…)
4. Link Prediction
対象nodeペア間にLinkがあるべきか否か、その2nodeの近隣トポロジーからpredictする。predictionというよりもinferenceの方がニュアンスが近い気がする。
今回評価に使用するアルゴリズムはPreferencial Attatchment(PA)だけする。Social-netにはPAの親和性がよい。
下記に定義あり。
ただ、どのアルゴリズムがよいのか一概にわからない。このpaperではどのToy dataにおいてもPAの精度が振るわず、なぜなのか考察されてあり興味深い。
この範囲を徐々に広範に広げていく手法はGlobal methodに分類される。有名なものにはKatz indexがある。
これらはheuristicな手法だが、流行りのGCNを使ったLink Predictionもある。
PAをfitする。
pa = PreferentialAttachment()
pa.fit(adjacency)
all_edges = [(i, j) for i in range(num_node) for j in range(num_node)]
y_true = is_edge(adjacency, all_edges)
scores = pa.predict(all_edges)
y_pred = whitened_sigmoid(scores)
予測精度はtraining dataを使って計る。なぜならPAをこのtraining dataにfitするとき予測対象Linkの存在は考慮していないため。
またLinkが存在しなかったところの予測精度も評価したいので、予測対象Linkは存在し得る全Link(=N x (N-1))とする。ただし両モデルともDensityが1%未満なので、非常にimbaranceなdataとなる点は考慮しなければならない。
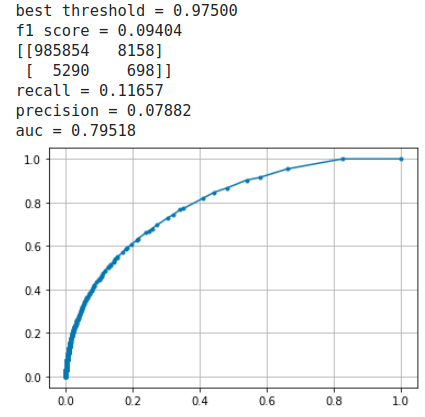
下記ではROCを描いてAUCを求め、またF1 scoreが最大となるように最適化し、その時の確率しきい値からConfusion matrixを求めている。
from sklearn.metrics import f1_score
from scipy.optimize import minimize
from sklearn.metrics import confusion_matrix
roc = metrics.roc_curve(y_true, scores, pos_label=True)
y_pred_arr = np.array(y_pred)
def f1_opt(x):
return -1 * f1_score(y_true, y_pred_arr >= x)
result = minimize(f1_opt, x0=np.array([0.5]), method='Nelder-Mead')
best_thresh = result['x'].item()
print('best threshold = {:.5f}'.format(best_thresh))
y_pred_arr = np.array(y_pred)
f1score = f1_score(y_true, y_pred_arr > best_thresh)
print('f1 score = {:.5f}'.format(f1score))
y_pred2 = []
for prob_ in y_pred:
if prob_ > best_thresh:
y_pred2.append(1)
else:
y_pred2.append(0)
cm = confusion_matrix(y_true, y_pred2)
print(cm)
recall = cm[1,1]/(cm[1,1] + cm[1,0])
precision = cm[1,1]/(cm[1,1] + cm[0,1])
print('recall = {:.5f}'.format(recall))
print('precision = {:.5f}'.format(precision))
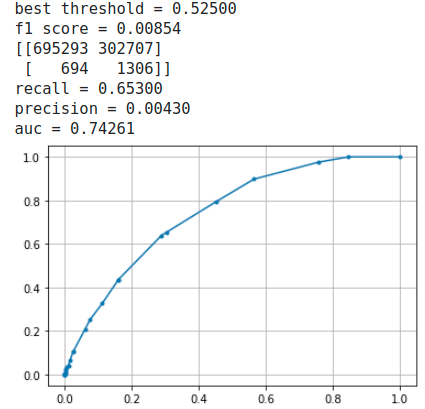
両方ともrecallもprecisionも悪いが、1%も無い「Linkあり」を予測するのだから仕方ない。Under samplingの方法も思いつくが、見てくれの精度が大きくなるだけで本質的ではないのでここでは行わない。
比較すると後者のFalse Negativeが非常に大きくなっており(低precision)、またAUCも小さい。しかしこれだけでwatts strogatz modelのトポロジーはLink Predictionに不適とも言い切れない。
軽微なエラーが途中で発生するが、random modelであるerdos renyi modelの結果は下記である。
erdos renyi model
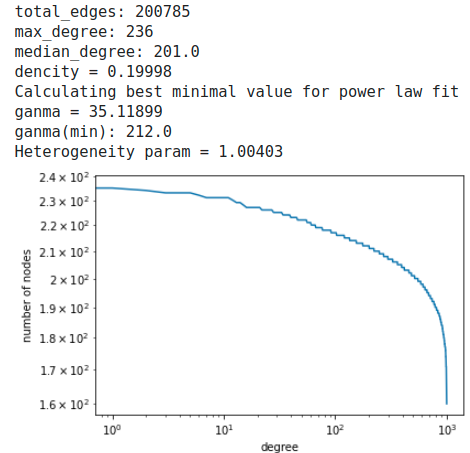
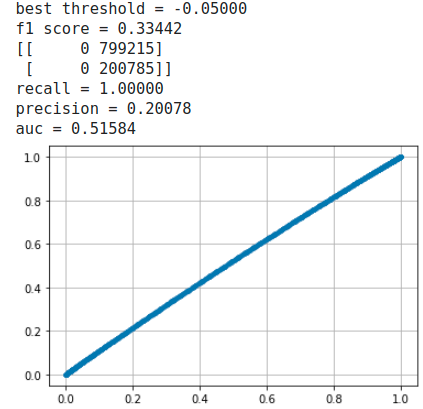
やはりrandom graphでは全く予測できていない。
5. まとめ
本当はScale-free network(2<ganma<3)でなければLink Predictionは適さないことを追確認したかったのだが、中途半端な結果となってしまった。まぁ、色々とパラメータを変えてもwatts strogatz modelの方が精度が悪かったので、それが救いか。
言えることは、Link PredictionするときはグラフがScal-freeか確認したほうがいいね、くらい。
6. 参考
graph theroyは初学だったので下記で勉強した。
この本は実践的で秀逸。数式を用いた説明よりも、そのmetricsが必要とされる背景から説明する和書では絶対にないスタイル。
下記はSocial-net界では重鎮のBarabasi先生が作成されたサイトで、これがあれば他の教科書は無用の長物だろう。
講義は有名なStanfordのCS224Wと、最近公開されたロシア国立HSEが勉強になった。
前者はGNNが最終目的で後者はGraph theory全般の講義
教材は各大学のサイトからDL可能
以上