FPGAで再帰的に総和を計算する
この記事ではverilogの再帰的なモジュールによる総和計算回路の実装方法を紹介します.
再帰的なモジュール
verilogでは再帰的にモジュールを定義することができます.
このことについては"verilogで再帰する"でも紹介しています.
再帰的にモジュールを定義することで,ツリー構造の回路を簡単に実装することができます.
回路の構造をツリーにすることで回路遅延を大幅に短縮することができます.
同じ演算を$n$個の値に適用する場合,演算回路の回路遅延は
- ラダー構造:$n$に比例して増加する
- ツリー構造:$\log n$に比例して増加する
という性質があります.
$$a \circ (b \circ c) = (a \circ b) \circ c$$
のように結合法則を満たす演算$\circ$は
$$((((((x_0 \circ x_1) \circ x_2) \circ x_3) \circ x_4) \circ x_5) \circ x_6) \circ x_7 \Rightarrow ((x_0 \circ x_1) \circ (x_2 \circ x_3)) \circ ((x_4 \circ x_5) \circ (x_6 \circ x_7))$$
のように演算順序を変更することができるので,演算回路をラダー構造からツリー構造に変換することができます.
加算,乗算,最大値,最小値,AND,ORなどの多くの演算はこの性質を持っています.
for文を使った総和計算回路(ラダー構造)
verilogではfor文を使って同じ演算を複数の数値に適用する反復処理を定義することができます.
for文を使って総和計算回路を実装すると,下に示すようなコードになります.
module SumLadders #
(
parameter WIDTH = 8,
parameter SIZE = 8
)
(
input wire [SIZE*WIDTH-1:0] idata,
output reg [WIDTH-1:0] odata
);
integer i;
always @(*) begin
odata = {WIDTH{1'b0}};
for (i = 0; i < SIZE; i = i + 1)
odata = $signed(odata) + $signed(idata[i*WIDTH+:WIDTH]);
end
endmodule
上のコードは図のようなラダー構造の回路を生成します.
再帰を使った総和計算回路(ツリー構造)
一方で,前述したようにverilogでは再帰的にモジュールを定義することができます.
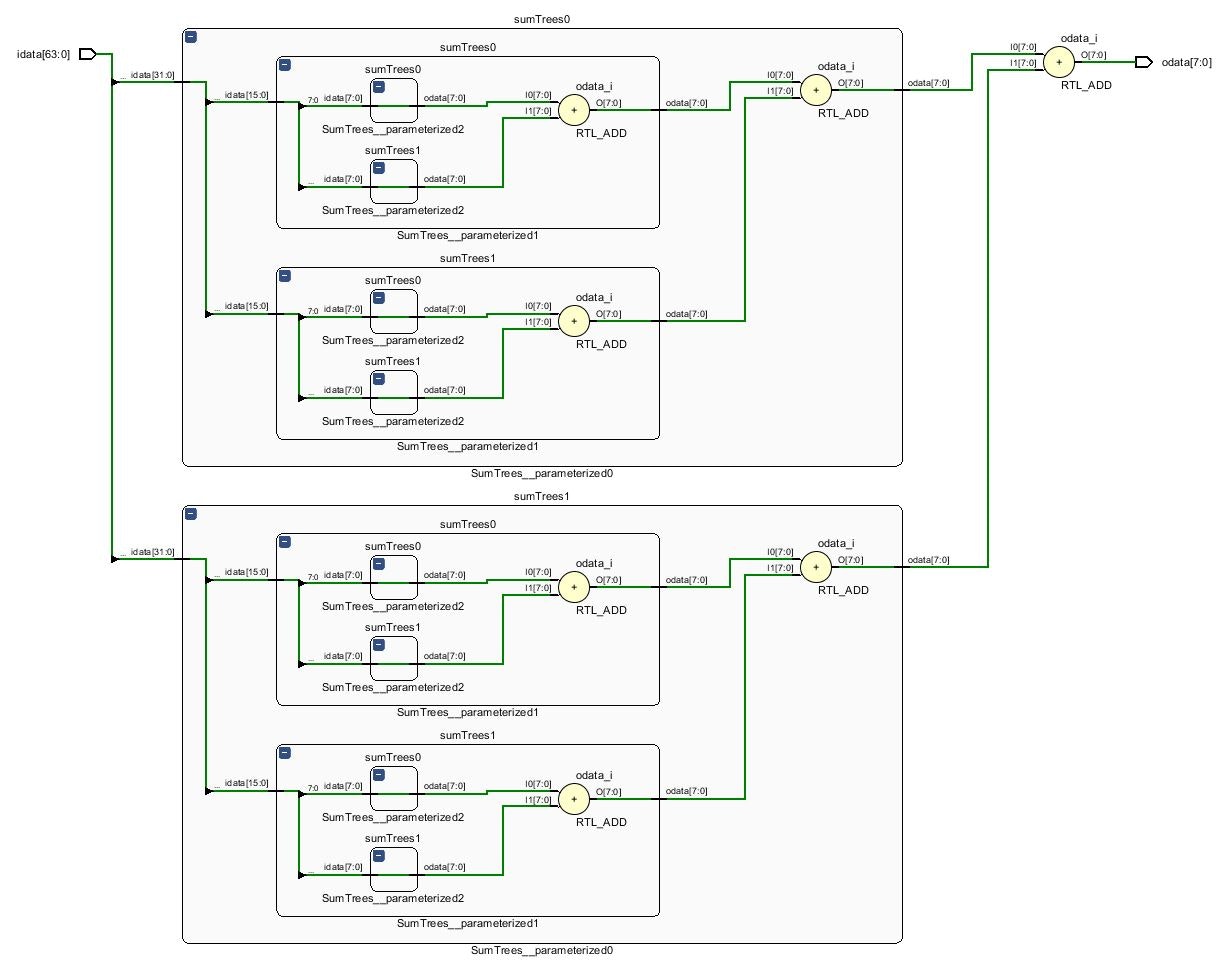
再帰的なモジュールを使って総和計算回路を実装すると,下に示すようなコードになります.
module SumTrees #
(
parameter WIDTH = 8,
parameter SIZE = 8
)
(
input wire [SIZE*WIDTH-1:0] idata,
output wire [WIDTH-1:0] odata
);
generate
if (SIZE == 1)
assign odata = idata;
else begin
localparam SIZE_L = SIZE >> 1;
wire [WIDTH-1:0] data0;
wire [WIDTH-1:0] data1;
assign odata = $signed(data0) + $signed(data1);
SumTrees #
(
.WIDTH(WIDTH),
.SIZE(SIZE_L)
)
sumTrees0
(
.idata(idata[SIZE_L*WIDTH-1:0]),
.odata(data0)
);
SumTrees #
(
.WIDTH(WIDTH),
.SIZE(SIZE_L)
)
sumTrees1
(
.idata(idata[SIZE*WIDTH-1:SIZE_L*WIDTH]),
.odata(data1)
);
end
endgenerate
endmodule
上のコードは下のようなツリー構造の回路を生成します.
桁上がりを考慮する
しかし,上の回路には問題があります.
数値の加算を行う場合には,桁上がりによる演算結果のオーバーフローを回避するためにビット幅を拡張する必要があります.
同じビット数の数値同士を加算する際には,元のビット幅に1ビット追加しなければなりません.
ツリー構造の加算回路ではツリーの階層ごとに追加しなければならないビット数が異なるため,必要なビット数を算出する必要があります.
ツリーの階層数は$\log_2 \mathrm{SIZE}$で表すことができるので,ビット拡張後の出力データのビット幅は
$clog2(SIZE)+WIDTH
となります.
また,下位モジュールの出力データのビット幅は,上位モジュールの場合と同様に,
$clog2(SIZE_L)+WIDTH
となります.
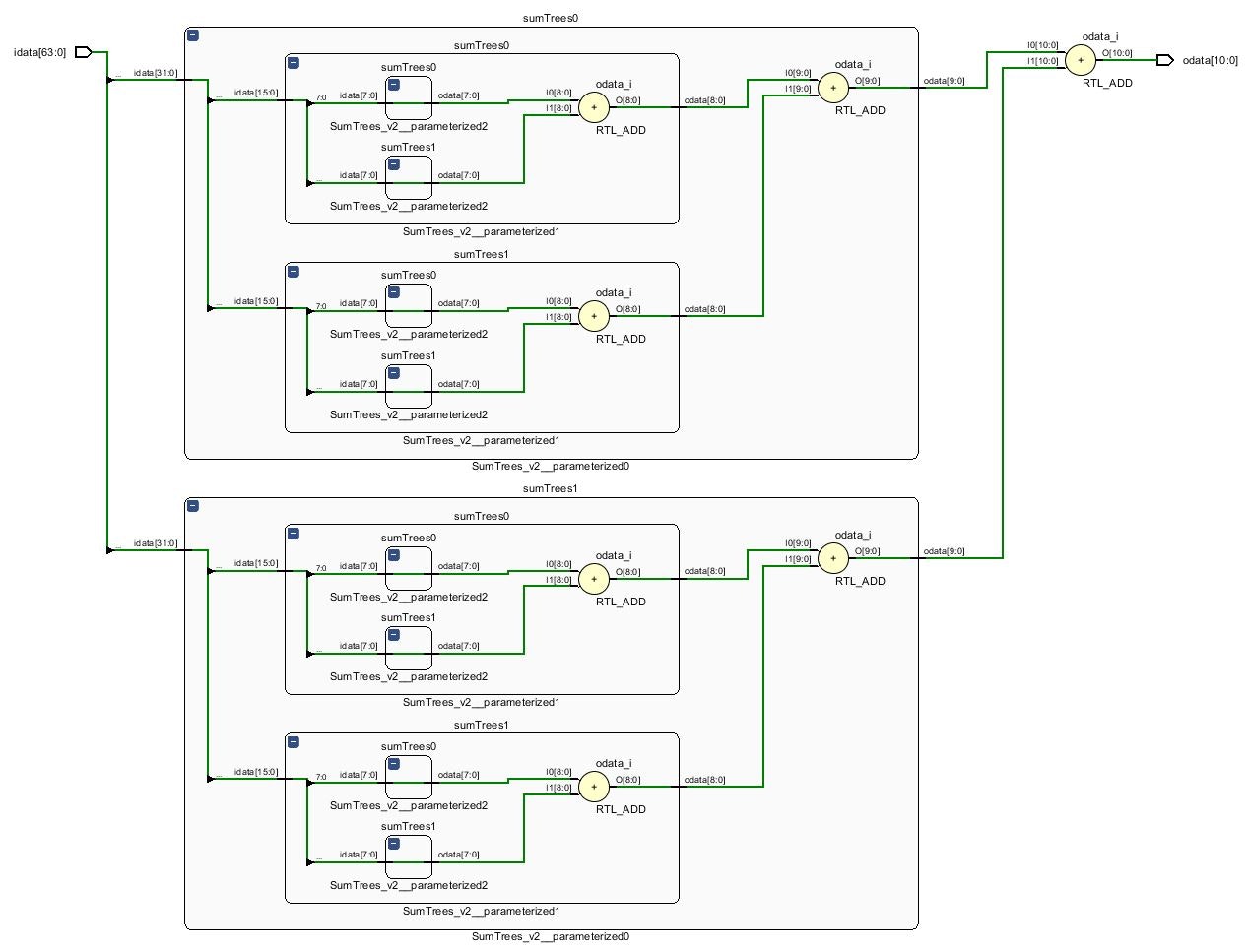
先ほどのコードに上記の変更点を加えると,下に示すようなコードになります.
module SumTrees_v2 #
(
parameter WIDTH = 8,
parameter SIZE = 8
)
(
input wire [SIZE*WIDTH-1:0] idata,
output wire [$clog2(SIZE)+WIDTH-1:0] odata
);
generate
if (SIZE == 1)
assign odata = idata;
else begin
localparam SIZE_L = SIZE >> 1;
wire [$clog2(SIZE_L)+WIDTH-1:0] data0;
wire [$clog2(SIZE_L)+WIDTH-1:0] data1;
assign odata = $signed(data0) + $signed(data1);
SumTrees_v2 #
(
.WIDTH(WIDTH),
.SIZE(SIZE_L)
)
sumTrees0
(
.idata(idata[(SIZE_L)*WIDTH-1:0]),
.odata(data0)
);
SumTrees_v2 #
(
.WIDTH(WIDTH),
.SIZE(SIZE_L)
)
sumTrees1
(
.idata(idata[SIZE*WIDTH-1:(SIZE_L)*WIDTH]),
.odata(data1)
);
end
endgenerate
endmodule
上のコードは図のような回路を生成します.
ツリーの階層が上がるごとにビット幅が1ビットずつ増えていることが分かります.
任意のサイズに対応させる
上の回路ではSIZEで指定できる数は2の冪乗に限られており,それ以外の数には対応していません.
2の冪乗はディジタル回路ではとても都合がいい数なので,2の冪乗のパラメータを前提に回路を設計する場合が多く,これはあまり大きな問題ではないかもしれません.
ですが,回路のパラメータを任意の自然数に対応させたい場合も考えられます.
その場合には,適切な下位モジュールのサイズをそれぞれ計算すればいいのです.
今回は,下位モジュールのサイズがそれぞれ,上位モジュールのサイズのおおよそ半分になるように下位モジュールのサイズを定義します.
下位モジュールのサイズをそれぞれ,SIZE_L0,SIZE_L1とすると,
localparam SIZE_L0 = SIZE - (SIZE >> 1);
localparam SIZE_L1 = SIZE - SIZE_L0;
となります.
この定義では必ずSIZE_L0はSIZE_L1よりも大きくなります.
この条件は,後で回路にレジスタを挟むときに必要となります.
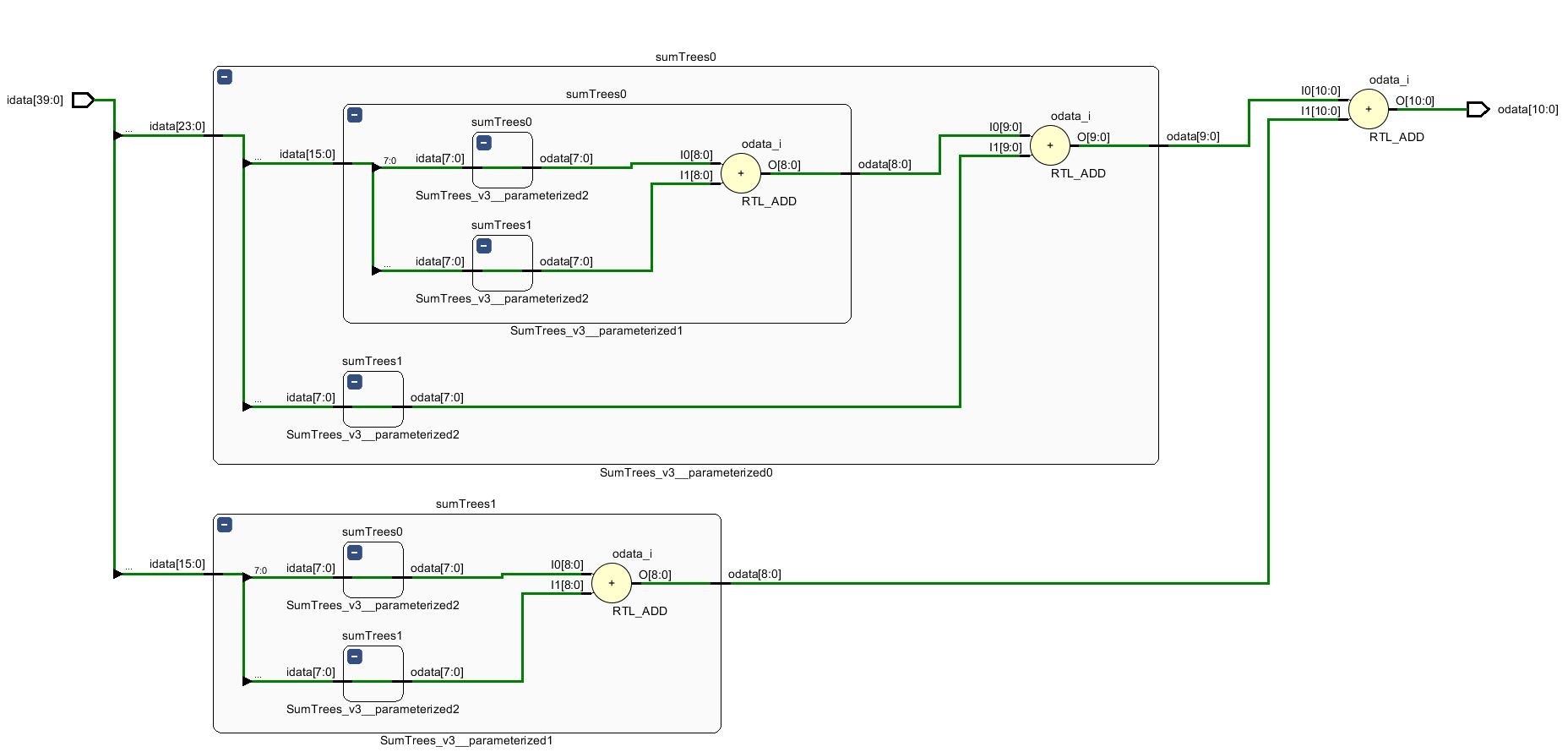
先ほどのコードに上記の変更点を加えると,下に示すようなコードになります.
module SumTrees_v3 #
(
parameter WIDTH = 8,
parameter SIZE = 5
)
(
input wire [SIZE*WIDTH-1:0] idata,
output wire [$clog2(SIZE)+WIDTH-1:0] odata
);
generate
if (SIZE == 1)
assign odata = idata;
else begin
localparam SIZE_L0 = SIZE - (SIZE >> 1);
localparam SIZE_L1 = SIZE - SIZE_L0;
wire [$clog2(SIZE_L0)+WIDTH-1:0] data0;
wire [$clog2(SIZE_L1)+WIDTH-1:0] data1;
assign odata = $signed(data0) + $signed(data1);
SumTrees_v3 #
(
.WIDTH(WIDTH),
.SIZE(SIZE_L0)
)
sumTrees0
(
.idata(idata[SIZE_L0*WIDTH-1:0]),
.odata(data0)
);
SumTrees_v3 #
(
.WIDTH(WIDTH),
.SIZE(SIZE_L1)
)
sumTrees1
(
.idata(idata[SIZE*WIDTH-1:SIZE_L0*WIDTH]),
.odata(data1)
);
end
endgenerate
endmodule
上のコードは図のような回路を生成します.
SIZEの値が2の冪乗以外でも正しく処理できていることが分かります.
レジスタを挟む
上の回路では,回路規模が大きくなるにつれて回路遅延が大きくなり,実装回路のパフォーマンスが低下します.
各演算器の間にレジスタを挟むことで,演算に必要なサイクル数(レイテンシ)を犠牲に実装回路のパフォーマンスを改善することができます.
しかし,これを実装するのは少し面倒です.
単に演算器の後ろにレジスタを配置しただけでは,下位モジュールのレイテンシの差によってデータのタイミングがずれてしまい,正しい演算結果が得られません.
この問題を解決するためには,下位モジュールのレイテンシの差を計算し,データのタイミングを調整する必要があります.
先ほど実装した回路では,必ずSIZE_L0がSIZE_L1よりも大きくなるように下位モジュールのサイズを定義しました.
これにより,1つ目の下位モジュールのレイテンシは必ず2つ目のものより大きくなります.
そのため,1つ目の下位モジュールの出力タイミングを基準に,2つ目の下位モジュールの出力をレジスタによって遅延させることで,データのタイミングを調整することができます.
下位モジュールのレイテンシ数は下位モジュールツリーの階層数と一致します.
下位モジュールツリーの階層数は$\log_2 \mathrm{SIZE_L}$で表されるので,
下位モジュールのレイテンシの差は,
localparam NB_DELAY = $clog2(SIZE_L0) - $clog2(SIZE_L1);
となり,これが遅延させなければならないサイクル数となります.
また,このサイクル数によって
- 0サイクル:遅延させない
- 1サイクル:単一レジスタによって遅延させる
- 2サイクル以上:シフトレジスタによって遅延させる
といった実装の切り替えが必要になります.
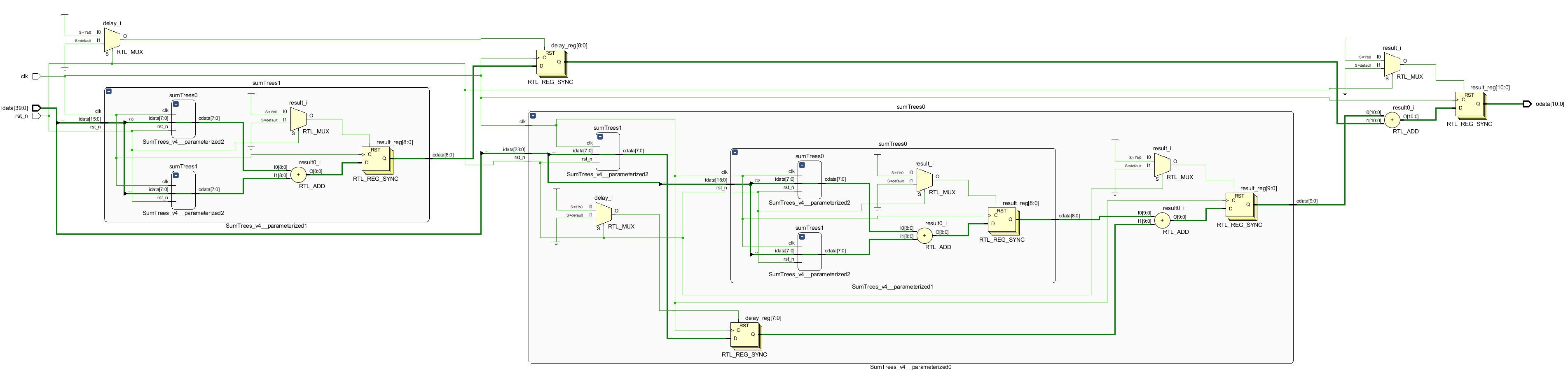
先ほどのコードに上記の変更点を加えると,下に示すようなコードになります.
module SumTrees_v4 #
(
parameter WIDTH = 8,
parameter SIZE = 5
)
(
input wire [SIZE*WIDTH-1:0] idata,
output wire [$clog2(SIZE)+WIDTH-1:0] odata,
input wire clk,
input wire rst_n
);
generate
if (SIZE == 1)
assign odata = idata;
else begin
localparam SIZE_L0 = SIZE - (SIZE >> 1);
localparam SIZE_L1 = SIZE - SIZE_L0;
localparam NB_DELAY = $clog2(SIZE_L0) - $clog2(SIZE_L1);
wire [$clog2(SIZE_L0)+WIDTH-1:0] data0;
wire [$clog2(SIZE_L1)+WIDTH-1:0] data1;
wire [$clog2(SIZE_L1)+WIDTH-1:0] data1_d;
reg [$clog2(SIZE)+WIDTH-1:0] result;
assign odata = result;
always @(posedge clk)
if (!rst_n)
result <= {$clog2(SIZE)+WIDTH{1'b0}};
else
result <= $signed(data0) + $signed(data1_d);
if (NB_DELAY == 0)
assign data1_d = data1;
else if (NB_DELAY == 1) begin
reg [$clog2(SIZE_L1)+WIDTH-1:0] delay;
assign data1_d = delay;
always @(posedge clk)
if (!rst_n)
delay <= {$clog2(SIZE_L1)+WIDTH{1'b0}};
else
delay <= data1;
end
else begin
reg [NB_DELAY*($clog2(SIZE_L1)+WIDTH)-1:0] delay;
assign data1_d = delay[$clog2(SIZE_L1)+WIDTH-1:0];
always @(posedge clk)
if (!rst_n)
delay <= {NB_DELAY*($clog2(SIZE_L1)+WIDTH){1'b0}};
else
delay <= {data1, delay[NB_DELAY*($clog2(SIZE_L1)+WIDTH)-1:$clog2(SIZE_L1)+WIDTH]};
end
SumTrees_v4 #
(
.WIDTH(WIDTH),
.SIZE(SIZE_L0)
)
sumTrees0
(
.idata(idata[SIZE_L0*WIDTH-1:0]),
.odata(data0),
.clk(clk),
.rst_n(rst_n)
);
SumTrees_v4 #
(
.WIDTH(WIDTH),
.SIZE(SIZE_L1)
)
sumTrees1
(
.idata(idata[SIZE*WIDTH-1:SIZE_L0*WIDTH]),
.odata(data1),
.clk(clk),
.rst_n(rst_n)
);
end
endgenerate
endmodule
上のコードは図のような回路を生成します.
少し分かりづらいですが,タイミング調節のためのレジスタが挿入されています.
AXI-Stream化する
AXI-Streamはシェイクハンドプロトコルで,演算回路IPコアのインターフェイスとしてよく使われています.
AXI-Streamでは,データのタイミングの調整はシェイクハンドプロトコルによって行われているため,先ほどの回路のようなタイミング調整は必要ありません.
ready信号の向きが逆であることに注意すれば簡単にツリーの回路を実装することができます.
単精度浮動小数点数の加算回路を使用した場合は下のようなコードになります.
module SumTrees_v5 #
(
parameter SIZE = 5
)
(
input wire [SIZE-1:0] ivld,
output wire [SIZE-1:0] irdy,
input wire [SIZE*32-1:0] idata,
output wire ovld,
input wire ordy,
output wire [31:0] odata,
input wire clk,
input wire rst_n
);
generate
if (SIZE == 1) begin
assign ovld = ivld;
assign irdy = ordy;
assign odata = idata;
end
else begin
localparam SIZE_L0 = SIZE - (SIZE >> 1);
localparam SIZE_L1 = SIZE - SIZE_L0;
wire vld0;
wire vld1;
wire rdy0;
wire rdy1;
wire [31:0] data0;
wire [31:0] data1;
FloatAdd floatAdd
(
.s_axis_a_tvalid(vld0),
.s_axis_a_tready(rdy0),
.s_axis_a_tdata(data0),
.s_axis_b_tvalid(vld1),
.s_axis_b_tready(rdy1),
.s_axis_b_tdata(data1),
.m_axis_result_tvalid(ovld),
.m_axis_result_tready(ordy),
.m_axis_result_tdata(odata),
.aclk(clk),
.aresetn(rst_n)
);
SumTrees_v5 #
(
.SIZE(SIZE_L0)
)
sumTrees0
(
.ivld(ivld[SIZE_L0-1:0]),
.irdy(irdy[SIZE_L0-1:0]),
.idata(idata[SIZE_L0*32-1:0]),
.ovld(vld0),
.ordy(rdy0),
.odata(data0),
.clk(clk),
.rst_n(rst_n)
);
SumTrees_v5 #
(
.SIZE(SIZE_L1)
)
sumTrees1
(
.ivld(ivld[SIZE-1:SIZE_L0]),
.irdy(irdy[SIZE-1:SIZE_L0]),
.idata(idata[SIZE*32-1:SIZE_L0*32]),
.ovld(vld1),
.ordy(rdy1),
.odata(data1),
.clk(clk),
.rst_n(rst_n)
);
end
endgenerate
endmodule
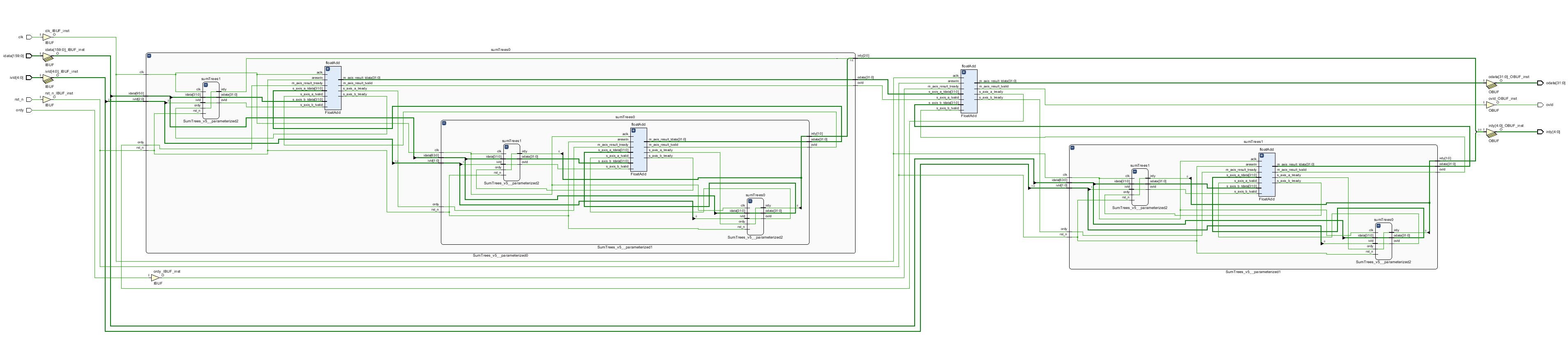
上のコードは図のような回路を生成します.
少し分かりづらいですが,AXI-Stream回路のツリーになっています.
まとめ
今回は再帰的なモジュールによる総和計算回路の実装方法を紹介しました.
再帰的なモジュールでは細かい回路パラメータの調節ができるので,複雑な構造の回路を簡単に実装することが可能です.