Mathematicaを使ってると、なんでそんな結果が返ってくるの?とか、どうしてこうなる?って思った事をつらづらと書いていきます。マニュアルやヘルプをちゃんと読んでいれば分かることも多いと思います。お気づきの点や、こうしたら良いよ、なんてのがありましたら教えてくだされば嬉しいです。あと別にWolfram社にMathematicaを治して欲しいと言ってる訳ではないです。。。注意点の忘備録とQiitaの練習のつもりで書いています。
1.Map(/@) はなんでリストだけなの?
例えば、
In[140]:= x = {a, b, c};
(#)^2 & /@ x
Out[141]= {a^2, b^2, c^2}
わかる。
In[141]:= x =.;
(#)^2 & /@ x
Out[142]= x
わからん。
なんでx^2になってくれないの! *Head[x]*がListでないとMapが機能しないのは理解してるのですが、結構間違えます。
2.ご破算で願いましては
Mathematicaでご破算で願いましては、*Clear[]*を使うのですが、
Clear["Global`*"];
と、いちいちClearと打ち込んで、Globalほげほげと全部で18打鍵もするのが面倒な事が多く・・・。しかもbacktick asteriskとか、わからんので久しぶりに使うと忘れている。
初期化なら複数カーネルを交互に再起動させる方法もあります。(Thanks kktk-KOさん)
3.時分秒や度分秒(°′″)で表示したい
角度(Degree)や時間(時分秒)などの計算は、ごく普通の電卓で良いという話もありますが、Mathematicaでやるなら時分秒で表示したいですよね~。現状は下記の様にしています。それと言うまでもありませんがMathematicaで角度はラジアンです。
In[769]:= Clear["Global`*"];
d = 2.50;(*10進数*)
t = {IntegerPart[#] "Hour",
IntegerPart[(FractionalPart[#]) 60] "Minute",
(FractionalPart[# 60 ]) 60 "Second"
} & /@ {d} // N
Out[770]= {{2. "Hour", 30. "Minute", 0. "Second"}}
わかる。
In[782]:= Clear["Global`*"];
d = 150/100;(*10進数*)
t = {IntegerPart[#] "Hour",
IntegerPart[(FractionalPart[#]) 60] "Minute",
(FractionalPart[# 60 ]) 60 "Second"
} & /@ {d} // N
Out[783]= {{"Hour", 30. "Minute", 0.}}
わからん。
1を略すなー! なお、*"Hour"などを消せば、ちゃんと1.が表示されます。
それとHead["Hour"]*はStringです。
In[784]:= Clear["Global`*"];
d = 0.50;(*10進数*)
t = {IntegerPart[#] "Hour",
IntegerPart[(FractionalPart[#]) 60] "Minute",
(FractionalPart[# 60 ]) 60 "Second"
} & /@ {d} // N
Out[785]= {{0., 30. "Minute", 0. "Second"}}
0時間(本当に0)だと数字の0に化けます。
3.1 対応策(Thanks kktk-KOさん)
3.1.1 DMSStringを使う。
十進記法による角θを度、分、秒の文字列に変換するのは、DMSStringで可能です。
In[74]:= DMSString[1.5]
Out[74]= 1°30'0.000"
3.1.2 ToStringを使う。
ToStringで数値を文字型にキャストする事が可能です。
In[116]:= Clear["Global`*"];
d = 150/100;(*10進数*)
t = {ToString[ IntegerPart[#] ] "Hour",
ToString[IntegerPart[(FractionalPart[#]) 60]] "Minute",
ToString[(FractionalPart[# 60] 60)] "Second"} & /@ {d} // N
Out[117]= {{"1" "Hour", "30" "Minute", "0" "Second"}}
4.オトナの四捨五入
最も近い a の倍数に四捨五入するには、Round[x,a]を使います。
In[1]:= Round[1.5,1]
Out[1]= 2
わかる。
In[2]:= Round[2.5,1]
Out[2]= 2
わからん。
なんで、2.5は四捨五入で3にならないの!?
In[36]:= Round[Table[n,{n,0,9}]+1/2]
Out[36]= {0, 2, 2, 4, 4, 6, 6, 8, 8, 10}
正の数は、0,2,4,6,8で切り捨てになります。
In[37]:= Round[-1(Table[n,{n,0,9}]+1/2)]
Out[37]= {0, -2, -2, -4, -4, -6, -6, -8, -8, -10}
負の数も同様です。
In[38]:= Limit[Round[Table[i,{i,0,9}]+1/2+n],n->0]
Out[53]= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
小数第一位が0.5でそれより下位の桁が0ではない時は切り上げます。
[](
プログラム言語や表計算ソフトでも色々な四捨五入があり、正の数の四捨五入と負の数の四捨五入が違うものもあります。また有効桁の丸め方や、お金の利息の丸め方など用途によって端数処理が違うことがあります。
不確かさを含む計測値の平均は自然を相手にします。お金やテストの点は人間を相手にします。私はMathematicaは前者よりであって欲しいです。
)
1990年の東工大後期のとある問題より
(x+1)(x-2) の小数第1位を四捨五入したものが 1+5x と等しくなるような実数 x を求めよ。
WolframAlphaでRound[(x+1)(x-2)]==(1+5x)として解くことができます。
4.1 数値的評価での四捨五入
数値的評価*N[]*は(本当に)四捨五入です。
In[1]:= 1 + 1 (10^-5) // N
Out[1]= 1.00001
*N[]*のデフォルトで表示される有効数値は6桁です。
In[24]:= 1 + 2 (10^-5) + 5 (10^-6) // N[#, 7] &
Out[24]= 1.000025
In[26]:= 1 + 2 (10^-5) + 5 (10^-6) // N[#] &
Out[26]= 1.00003
1.000025を有効数値6桁で表せば1.00003になります。
In[27]:= 1 + 2 (10^-5) + 5 (10^-6) // Round[#, 1/100000] & // N[#, 7] &
Out[27]= 1.000020
*Round[]*は偶数で丸め(切り捨て)ます。
4.2 不等式での四捨五入
次の不等式をMathematicaで解いてみます。
\frac{6.27x^2-8.93}{2.55} \leqq x
In[6555]:= Reduce[(6.27 x^2 - 8.93)/2.55 <= x, x]
Reduce::ratnz: Reduceは厳密でない係数の系を解くことができませんでした.解は対応する厳密系を解き,結果を数値に変換することで得られました. >>
Out[6555]= -1.00727 <= x <= 1.41397
Reduceは厳密でない係数の系を解くことができませんでした.解は対応する厳密系を解き,結果を数値に変換することで得られました.
という警告がでました。これは、式に含まれる係数6.27,8.93,2.55が厳密な数値では無いが、厳密な数値として扱って、結果を厳密でない数値に戻して下記の結果を得た事を警告しています。
-1.00727 \leqq x \leqq 1.41397
では、この警告を見てどーするのかと言うと、与式をひとまずは厳密な数値に変換してから、MathematicaでReduceしてみます。具体的には、6.27を627/100、893/100、255/100と数値を有理数にして与えます。
In[6556]:= Reduce[(627/100 x^2 - 893/100)/(255/100) <= x, x]
Out[6556]= (255 - Sqrt[2304669])/1254 <= x <= (
255 + Sqrt[2304669])/1254
答えは厳密値で、
\frac{255-\sqrt[]{2304669}}{1254} \leqq x \leqq \frac{255+\sqrt[]{2304669}}{1254}
となります。
最小値に注目して、これを数値化してみます。
In[6558]:= (255 - Sqrt[2304669])/1254 // N
Out[6558]= -1.00727
この-1.00727は厳密な数値ではありません。有効桁を1桁増やしてみます。
In[6561]:= (255 - Sqrt[2304669])/1254 // N[#, 7] &
Out[6561]= -1.007268
結果は-1.007268になりました。ここで、小数第6位を四捨五入するとすれば-1.00727になります。次に、この値(-1.007268)を与式のxに代入してみましょう。
In[6562]:= (627/100 (-1.007268)^2 - 893/100)/(255/100) <= (-1.007268)
Out[6562]= False
わからん。なんでFlase(偽)になるんだー(TT
不等式の数値化する時は、xの範囲を考えて四捨五入をしないとダメですが、これはMathematicaはやってくれません。負の最小値<=x <=正の最大値の場合、数値化するときは四捨五入ではなく、人間が手動で切り捨をします。-1.007268は、有効数字8桁で表わせば、-1.0072676です。これを有効数字7桁で丸める時は切り捨てます。-1.007267を与式に代入してみます。
In[6565]:= (255 - Sqrt[2304669])/1254 // N[#, 8] &
(627/100 (-1.007267)^2 - 893/100)/(255/100) <= (-1.007267)
Out[6565]= -1.0072676
Out[6566]= True
すると、不等式がTrue(真)になり、成り立つ事がわかります。
なので、有効数値6桁で答えを求めると
-1.00726 \leqq x \leqq 1.41396
となります。なんでもMathematicaに任せて、四捨五入しないように気をつけましょう。
4.3 米ドルでの四捨五入
$547.03(五百四十七ドル 三セント)の品物を九十五個購入するには、いくら必要でしょうか?
In[1051]:= 547.03 95
Out[1051]= 51967.9
Mathematicaで計算すると$51967.9(五万一千九百六十七ドル 九十セント)?となりましたが、実は答えは、
In[1054]:= 54703/100 95 // N[#, 8] &
Out[1054]= 51967.850
**$51967.85(五万一千九百六十七ドル 八十五セント)**です。
うっかり小数点表記のままで入力してしまうと近似計算となり下記の様に正しく計算ができません。
In[1055]:= 547.03 95 // N[#, 8] &
Out[1055]= 51967.9
しかし途中にRoundを挟んでセントの(1/100)単位を指定すれば計算してくれます。
In[1057]:= 547.03 95 // Round[#, 1/100] & // N[#, 8] &
Out[1057]= 51967.850
しかし油断して、最後に*//N*で近似計算してしまうと下記の様に四捨五入されてしまいます。
In[1058]:= 547.03 95 // Round[#, 1/100] & // N
Out[1058]= 51967.9
ちなみにWolfram Alphaで$$547.03を95倍すると、$$51970になり、二ドル十五セントも損をします。オトナ買いデスネ。気をつけましょう。。。
5. 一様分布はなんで閉区間なの?
一様分布(Google検索 979,000件)、矩形分布(同 550,000件)でした。平成28年4月6日現在。
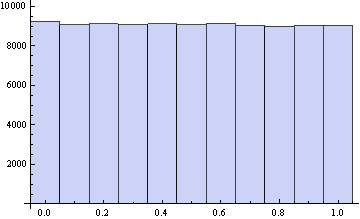
一様分布でヒストグラムを作成します。
In[74]:= Histogram[ RandomReal[UniformDistribution[{-5/100, 105/100}], 100000], {-5/100, 105/100, 1/10}]
乱数の最大値と最小値を調べます。
In[75]:= {Min[#], Max[#]} & @ RandomReal[UniformDistribution[{-5/100, 105/100}], 1 000 000]
Out[75]= {-0.0499999, 1.05}
わからん。なんで100万回もやってるのに-0.05が来ないんだー。気をつけましょう。(涙
5.1 離散化して一様分布させる。
*RandomChoice[]*を使用すればリストに含まれる要素をランダムに選択する事ができます。
リストの要素は-1.05から+1.05まで0.01刻みの211個とします。10万回も繰り返せば全要素均等に発生するでしょう。
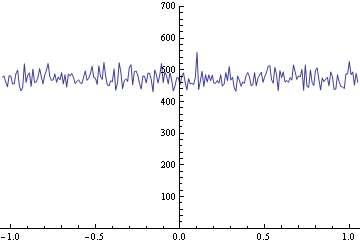
RandomChoice[]でヒストグラムを作成します。離散値なのでListLinePlotを使います。
In[76]:= s = RandomChoice[Table[n/100, {n, -105, 105, 1}], 100000];
Tally[s] // Sort // N // ListLinePlot[#, PlotRange -> {{-1.06, 1.06}, {0, 700}}] &
ここで最も近い10^iの倍数に(本当に)四捨五入する関数fを定義します。但しiは任意の整数とさせてください。
In[73]:= f[x_, n_: 1] := Piecewise[{
{Ceiling[x n^-1] n, FractionalPart[x n^-1] >= 1/2},
{IntegerPart[x n^-1] n,
FractionalPart[x n^-1] > -1/2 && FractionalPart[x n^-1] < 1/2},
{Floor[x n^-1] n, FractionalPart[x n^-1] <= -1/2}
}
];
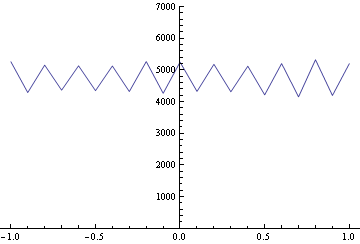
そして先ほどRandomChoiceで生成した乱数を四捨五入したヒストグラムを作成します。
In[74]:= Tally[ f[#, 1/10] & /@ s] // Sort //
ListLinePlot[#, PlotRange -> {{-1.06, 1.06}, {0, 7000}}] &
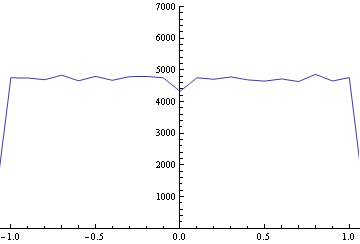
四捨五入ではグラフから分かる様に、0の度数が4,326と他に比べて小さくなっています。また-1.1の度数が507、+1.1の度数が439でした。
比較のため*Round[]*したヒストグラムを作成します。
In[75]:= Tally[ Round[#, 1/10] & /@ s] // Sort //
ListLinePlot[#, PlotRange -> {{-1.06, 1.06}, {0, 7000}}] &
離散化した数値を*Round[]*してヒストグラムを取るとキザキザになり丸めた数は偶数に偏ります。
-1.1と+1.1の度数は0になります。(Roundは、-1.05と+1.05が小数第一位の0のため切り捨てで±1.0になる。四捨五入は±1.1になる。)
また0の度数は他と比べて均一になっています。
5.2 丸め方による平均値の違い。
丸めなし、Round[]、四捨五入の3種類での平均値を比較してみます。
-1.05から+1.05までの一様分布の実数データ1千万個で平均を比較します。
In[41]:= SeedRandom[1];
s = RandomReal[UniformDistribution[{-105/100, 105/100}], 10000000];
Mean[s]
Mean[Round[#, 1/10] & /@ s]
Mean[f[#, 1/10] & /@ s]
Out[43]= 0.0000648334
Out[44]= 2419/50000000
Out[45]= 2419/50000000
四捨五入の平均値と*Round[]*の平均値を比較すると同じでした。
次に5.00から5.19まで0.01刻みのデータ20個で平均を比較してみます。
In[55]:= s = Table[n/100, {n, 500, 519}];
Mean[s] // N
Mean[Round[#, 1/10] & /@ s] // N
Mean[f[#, 1/10] & /@ s] // N
Out[56]= 5.095
Out[57]= 5.095
Out[58]= 5.1
四捨五入の平均値はわずかに上に偏ります。
今度は5.00から5.19までの一様分布の実数データ1千万個で平均を比較してみます。
In[60]:= SeedRandom[1];
s = RandomReal[UniformDistribution[{5, 519/100}], 10000000];
Mean[s]
Mean[Round[#, 1/10] & /@ s]
Mean[f[#, 1/10] & /@ s]
Out[62]= 5.09501
Out[63]= 15921043/3125000
Out[64]= 15921043/3125000
四捨五入の平均値と*Round[]*の平均値を比較すると同じでした。
最後にRandomChoiceで5.00から5.19まで0.01刻みのデータ20個を一様分布で1千万個選び平均を比較してみます。
In[70]:= SeedRandom[1];
s = RandomChoice[Table[n/100, {n, 500, 519, 1}], 10000000];
Mean[s]
Mean[Round[#, 1/10] & /@ s]
Mean[f[#, 1/10] & /@ s]
Out[72]= 1273750743/250000000
Out[73]= 12737499/ 2500000
Out[74]= 127500257/ 25000000
In[75]:= {%72,%73,%74}//N
Out[75]= {5.095, 5.095, 5.10001}
四捨五入の平均値はわずかに上に偏ります。
[](
Roundと四捨五入の平均値を比較すると下記がわかりました。
実数データの一様分布のデータについては、少なくとも平均値で見れば偏りは認められない。
小数第2位のデータを小数第一位に丸める場合については、四捨五入の平均値は上に偏る。
## 5.3 Roundと四捨五入の平均値の比較まとめ
関数電卓が四捨五入である事、人間がデータを吟味する時のやりやすさを考えれば、私は小学校で習った四捨五入を使うのが良いと考えます。
)
6.精度と確度と、測定不確かさ
Mathematicaでは10÷3は3分の10という有理数になります。その精度は∞で、真値または厳密数で結果を表示しようとします。
In[89]:= 10/3
Out[89]= 10/3
In[90]:= Precision[%89]
Out[90]= ∞
わかる。
Roundで小数点以下を丸めて、精度を見ます。
In[91]:= Round[10/3]//Precision
Out[91]= ∞
わからん。なんで精度は∞のままなのか?
6.1 測定データを読み込む
ここでMathematicaに実際に測定したデータを読み込ませて見ます。
Directory[] <> "\Mathematica\GPIB" // SetDirectory
s = Import["gpib01a.log.gz"];
これで測定データをリストsに読み込みます。
gpib01a.log.gzは100Ωの抵抗を21600回測定した結果をgzip圧縮したテキストファイルです。ファイルの内容は下記の様なCSV形式です。
+100.00453E+00ROHM4W,12:13:30.38 13-Apr-2016,+51069RDNG#,00EXTCHAN , +1.02237860E+02
+100.00440E+00ROHM4W,12:13:32.49 13-Apr-2016,+51090RDNG#,00EXTCHAN , +1.02323340E+02
読み込んだ1行目の内容を確認します。
In[8]:= s[[1]]
Out[8]= {"+100.00453E+00ROHM4W", "12:13:30.38 13-Apr-2016", "+51069RDNG#", \
"00EXTCHAN ", 102.238}
可視化に適した形に変換をかけます。
p = {StringJoin[StringCases[#[[3]], RegularExpression["\\d"]]],
StringTake[#[[1]], {1, 1 + 9}] <> "`8.5 10^(" <>
StringTake[#[[1]], {1 + 11, 1 + 11 + 2}] <> ")" // ToExpression,
DateList[(AbsoluteTime[DateList[#[[2]]]] + 46563)] , #[[5]]} & /@
s[[1 ;;]];
内容を確認します。
In[9]:= p[[1]]
Out[9]= {"51069", 100.004530, {2016, 4, 14, 1, 9, 33.38}, 102.238}
6.2 測定値を可視化する
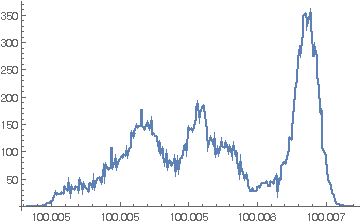
まず、ヒストグラムを作成してみます。
# [[2]] & /@ p[[1 ;;]] // Tally // Sort // ListLinePlot
横軸が測定値(単位[Ω])、縦軸が度数(単位[回])です。で、横軸をよく見ると・・・ Tallyを使っているからか、100.005Ωが3回横軸に現れてしまいます。そこで、ListLinePlotではなく、Histogramを使って作成してみます。
# [[2]] & /@ p[[1 ;;]] // Histogram
ワカラン。なんで、ヒストグラムでも100.005Ωが3回も出てくるんだ~(TT 100.005が複数でてくるので、横軸の比率が崩れています。。。気をつけましょう。
6.3 統計値を求める
気を取り直して、測定結果の統計値を取ってみます。
In[37]:= #[[2]] & /@ p[[1 ;;]] // Min (* 最小値 *)
# [[2]] & /@ p[[1 ;;]] // Max (* 最大値 *)
# [[2]] & /@ p[[1 ;;]] // Mean (* 平均値 *)
# [[2]] & /@ p[[1 ;;]] // StandardDeviation (* 標準偏差 *)
# [[2]] & /@ p[[1 ;;]] // Variance (* 分散 *)
Out[37]= 100.004320
Out[38]= 100.006690
Out[39]= 100.005709
Out[40]= 0.000560
Out[41]= 3.13*10^-7
分散ですが、Mathematicaでは不偏推定量の分散を求めるので(N-1)で割った値が算出されますので気をつけてください。標準偏差も同様です。
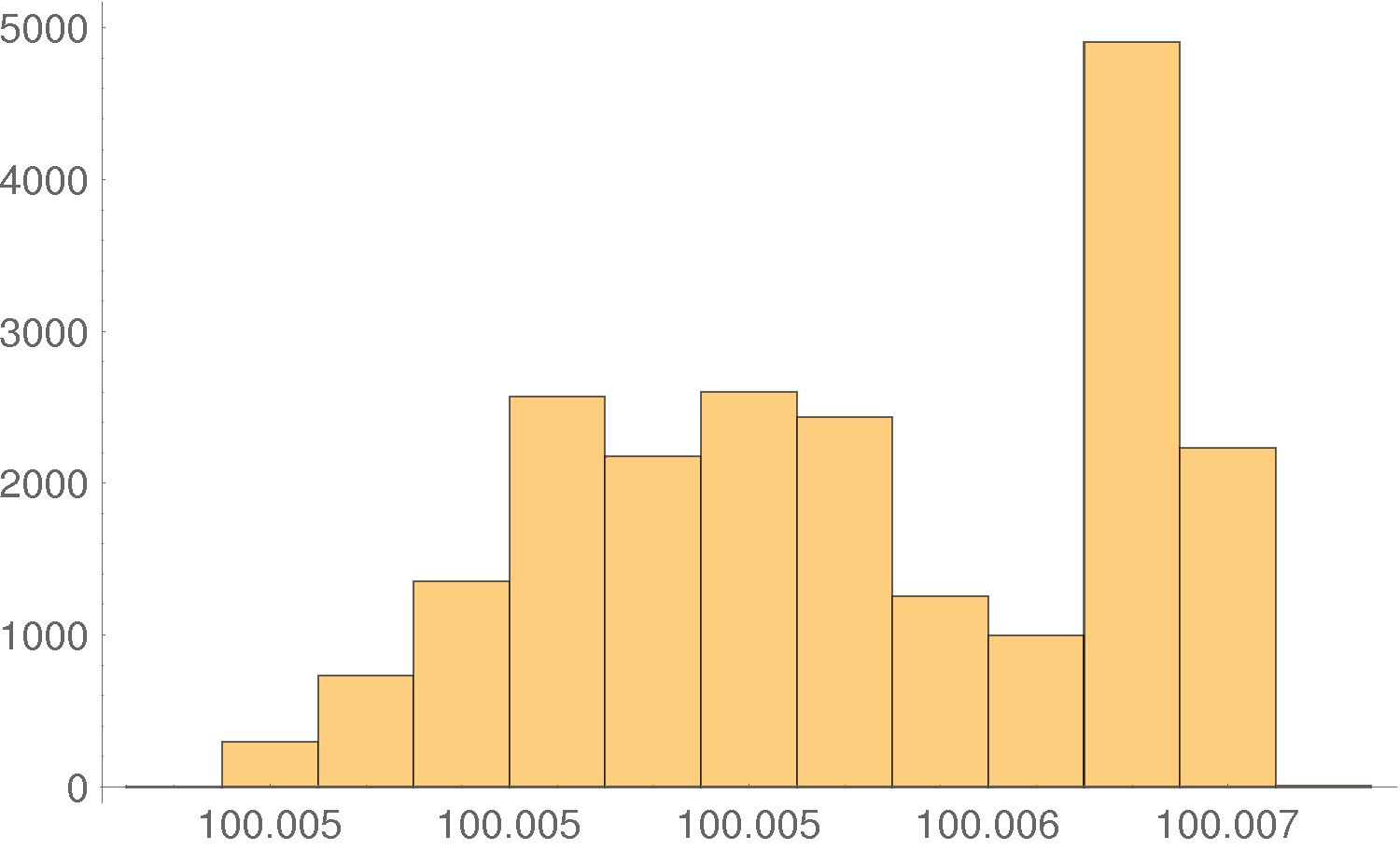
6.4 BinCountsでヒストグラムを可視化する。
Tallyではなく、BinCountsで、さらに横軸を-100Ωして、ヒストグラムを作成してみます。
# [[2]] & /@ p[[1 ;;]] //
BinCounts[#, {100004/1000, 100007/1000, 5/100000}] & //
Riffle[Table[n, {n, 4, 7, 5/100}], #] & //
Partition[#, 2] & // ListLinePlot
統計値が最小値100.0043Ω、最大値が100.006690Ωで、上図と合ってます。
測定値をヒストグラムにする時はBinCountsを用いるのが分かりやすいですね。
6.5 誤差解析
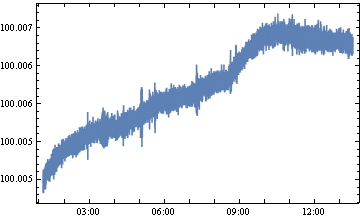
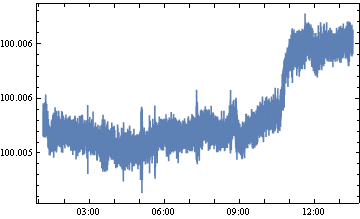
次に誤差解析をしていきます。横軸を測定時刻、縦軸を測定値にしたグラフを作成してみます。
{#[[3]], #[[2]]} & /@ p[[1 ;;]] // DateListPlot
つぎに測定開始時刻と終了時刻を求めます。
In[105]:=p[[1]][[3]] // DateString
p[[-1]][[3]] // DateString
Out[105]="Thu 14 Apr 2016 01:09:33"
"Thu 14 Apr 2016 13:31:53"
測定誤差の発生原因としては、まず温度変化が考えられます。そこで、測定した環境での温度データを読み込みます。
In[106]:=q = Import["mw100.log.gz"];
p1 = {Round[DateList[#[[1]]]], #[[2]], #[[3]], #[[4]], #[[5]], #[[
6]], #[[7]], #[[8]]} & /@ q[[1 ;;]];
In[107]:=p1[[1]]
Out[107]={{2016, 4, 13, 20, 6, 20}, 254, 250, 248, 254, 241, 86, 0}
使うデータは1列目の日付と2列目の温度 (1/10 ℃)です。254は25.4℃を表します。
抵抗値を測定したリストには測定時刻が入っています。その測定時刻での温度データを取得して、リストにJoinします。
r = AbsoluteTime /@ p1[[All, 1]] // Round;
q = Join[#,
p1[[(Position[r, Round[AbsoluteTime[#[[3]]]]])[[1]], 2]] /10.0 ] & /@ p;
r =.;
In[121]:= q[[1]]
Out[121]= {"51069", 100.004530, {2016, 4, 14, 1, 9, 33.38}, 102.238, 24.6}
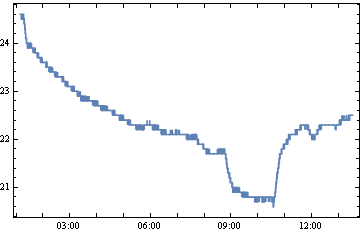
横軸を測定時刻、縦軸を温度にしたグラフを作成してみます。
{#[[3]], #[[5]]} & /@ q // DateListPlot
6.6 温度で誤差を補正する
抵抗値の温度変化を補正してみます。温度23℃の1次温度係数5ppm/℃、2次温度係数0.1ppm/℃として計算し、リストにJoinしてみます。
t = Join[#, {#[[2]] (1 + 5/10^6 (#[[5]] - 23.0) + 0.1/10^6 (#[[5]] - 23)^2 )}] & /@ q;
In[125]:= t[[1]]
Out[125]= {"51069", 100.004530, {2016, 4, 14, 1, 9, 33.38}, 102.238, 24.6, 100.005}
横軸を測定時刻、縦軸を温度補正した測定値のグラフを作成してみます。
{#[[3]], #[[6]]} & /@ t[[1 ;;]] // DateListPlot
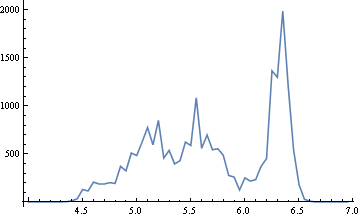
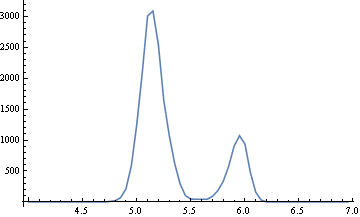
ヒストグラムを作成してみます。
# [[6]] & /@ t[[1 ;;]] //
BinCounts[#, {100004/1000, 100007/1000, 5/100000}] & //
Riffle[Table[n, {n, 4, 7, 5/100}], #] & // Partition[#, 2] & //
ListLinePlot[#, PlotRange -> All] &
2つ山がありますが、分散は生データより減りました。横軸は100Ωを差し引いていて、単位は[mΩ]です。最頻値は100.00515Ωで、度数は3089です。
6.8温度と電気抵抗の相関関係
測定環境の温度と抵抗値は関係あるの? 電気の教科書に書いて有ります!だと、話が終わってしまいますので相関関係を取ってみます。
どこの企業にもあるMS-Excelでは散布図を使います。Mathematicaでも同じ事ができます。横軸に温度、縦軸に抵抗値でプロットしてみます。
pl3 = {#[[2]], #[[5]]} & /@ t // ListPlot
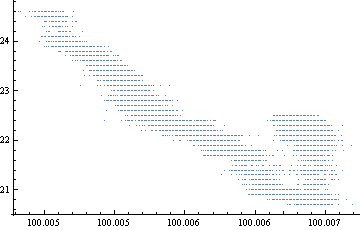
温度22℃付近で測定値が2つに割れていますが、概ね温度が下がると抵抗値が比例して(直線的に)増加する事が散布図から分かります。抵抗線の素材はマンガニン線です。
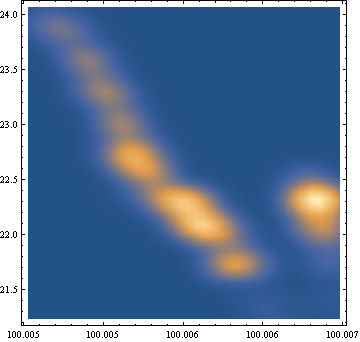
測定データが大量にある時に散布図ですと、その度数がどの位あるか分からなくなります。できればヒストグラムの様な散布図が欲しい所ですが、MathematicaにはSmoothDensityHistogramが用意されています。
pl4 = {#[[2]], #[[5]]} & /@ t // SmoothDensityHistogram
測定中の温度は22℃が多かったのでその付近のデータが沢山取れていることが色で読み取れて便利ですね。
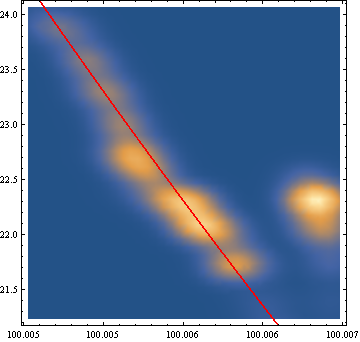
次に温度補正した抵抗値を赤線でプロットした図を重ね合わせてみます。
pl5 = {#[[7]], #[[5]]} & /@ t // ListLinePlot[#, PlotStyle -> Red] &;
Show[pl4, pl5]
つづく!
7.東京23区
ご存じの様に我が国の首都である東京には26市, 5町, 8村と23区があります。Mathematicaで23区をリストで登録していきましょう。
tokyoku = {葛󠄂飾区};
イキナリ最初が何故に葛飾区なのか・・・ではなくて、字形が旧字体「葛󠄂」󠄂になってしまいます。(Windows XPとRaspberry PIの場合 平成28年4月現在)
これはOS側のフォントですとか、常用漢字のオトナな事情が原因でMathematicaが原因ではありません。
MathematicaではVer.3辺り(?)からUnicode対応しています。例えば、\:845bと打ち込むと葛と入力できます。なのでUTF-16と思われますが、円周率πなどの数学記号等は注意が必要です。
UnicodeのIVS(Ideographic Variation Sequence)に対応して貰えると葛の字や、あと牛丼の吉野家もちゃんと土口の吉と表示できるようになるんぢゃないかなぁと思います。たまに人名でツチヨシの人が居て電子メールで困る事がありますよね?
似たような問題ですが、円周率のπはMathematicaからメモ(Windowsならメモ帳、Macならメモ、ラズパイなら何故かEmacs)にコピペすると\[Pi]にMOJIBAKEします。
Unicodeでは色々なEMOJIが使えます。例えばDiceとか面白いですよね。
In[81]:= dice = {\:2680,\:2681,\:2682,\:2683,\:2684,\:2685};
RandomChoice[dice,2]
Out[81]= {⚁, ⚀}
MacとRasberryPiは表示できますけど、Windows XPとWindows7辺りは怪しいです。MS-Word上でフォントを選べばEMOJIが使えたりする事があります。
このような文字は、機種依存文字ということで半角カタカナと同様に使用禁止にするのがネチケットでしょうか。というかShiftJISには苦労いたしました。(TT
苦労したく無い場合は、アルファベットだけを使用するのが良いと思いますが、可読性から言えば位相差のφや角速度ωあたりは使いたいですよねぇ。あと地名をアルファベットで表す時は群馬県(訓令式"Gunma"、ヘボン式"Gumma”)に気をつけてください。
7.1 旧字体の葛
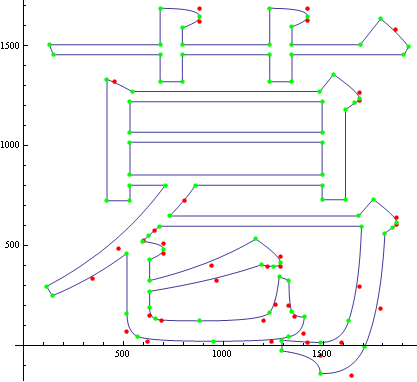
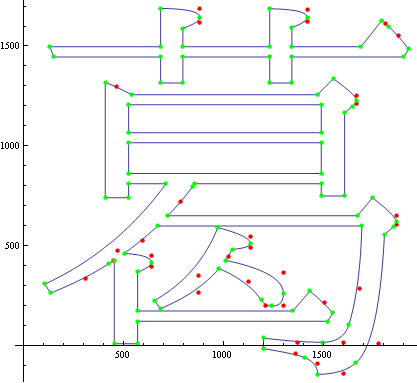
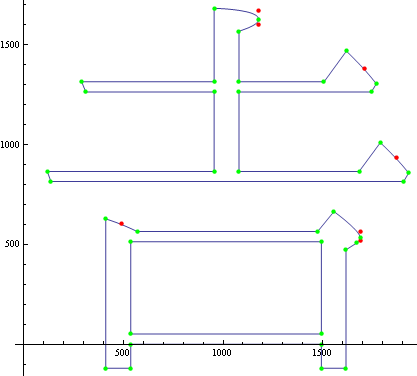
この文章はQiitaのKobitoというエディタで編集しているのですが、コード領域では旧字、テキスト領域では新字体で表示されています。しかし、Webブラウザで見ると、どちらも新字体になってました。とほほ。Mathematicaはベジェ曲線を扱えますので、TrueType Fontを可視化してみました。使用した日本語フォントはIPAmj明朝フォントです。
7.2 つちよし
あ。つちよし「𠮷」はWebブラウザで表示できますね。
7.3 TrueType FontをMathematicaで可視化する。
TrueType Fontを可視化してみます。まず前準備として、IPA mj FontとFont UtilityのTTXとgawkを用意します。
例として、ひらがなの「あ」を可視化しています。「あ」はUnicodeのUTF-16でU+3042です。
まずttxを使用して、下記コマンドを実行します。
ttx ipamjm.ttf
これでipamjm.ttfをipamjm.ttxへ変換します。そしてお好みのテキストエディタでipamjm.ttxを開いて「あ」のUnicodeの0x3042を検索します。
<map code="0x3042" name="aj843"/><!-- HIRAGANA LETTER A -->
<map code="0x3043" name="aj844"/><!-- HIRAGANA LETTER SMALL I -->
すると、上の様なコードが検索に引っかかります。name=の部分がGlyph(文字の形)の名前になります。Glyphの名前、aj843を検索します。幾つか他の場所が検索に掛かりますが、下記の様なコードを探します。
<TTGlyph name="aj843" xMin="252" yMin="-66" xMax="1804" yMax="1620">
<contour>
<pt x="1180" y="977" on="1"/>
<pt x="1160" y="1040" on="0"/>
<pt x="1110" y="1077" on="1"/>
<pt x="1143" y="1114" on="1"/>
<pt x="1233" y="1076" on="0"/>
<pt x="1290" y="975" on="1"/>
<TTGlyph>から</TTGlyph>までが「あ」のGlyphになります。この部分(202行ほどあります。)をコピペして別ファイルにa.txtというファイル名で保存します。
a.txtをMathematicaのリスト形式に変換します。変換にはgawkを使いました。コードを下記に示します。
BEGIN{
printf("{\n");
}
/\<\contour\>/ {
l=length($1);
if(l==9) {
printf(" {\n");
} else {
printf(" },\n");
}
}
/\<\/contour\>/ { #umaku ugokanai
print $0;
printf(" },\n");
}
/\<pt x=/ {
x=$2;
l=length(x);
x=substr(x,4,l-4);
y=$3;
l=length(y);
y=substr(y,4,l-4);
f=$4;
l=length(f);
f=substr(f,5,l-5);
printf(" {%d,%d,%d},\n",x,y,f);
}
END {
printf("}\n");
}
上記のコードを例えばglyph.awkとして保存しておきます。次にコマンドラインから、
gawk -f glyph.awk a.txt >a.m
として、変換をします。変換後に、a.mをテキストエディタで開き、}, }の余計なカンマを削除します。「あ」の場合は、全部で4カ所あります。
{1110,735,1},
{1172,826,0}, ←ここの行末のカンマをとる。
},
{
{787,352,1},
{761,541,0},
TrueType Fontの変換は以上です。
次にMathematicaを起動して下記のコードを入力します。
Gryph2[pt_, t_] := Module[
{pn, i, n, p, pta, ptb, len, r, ret, f, t1},
pn = Length[pt];
i = 1;
ret = {};
If[NumberQ[t], , Return[{{Null, Null}, {Null, Null}}]];
While[i <= pn,
p = Append[pt[[i]], pt[[i, 1]]];
pta = p[[All, 1 ;; 2]];
ptb = p[[All, 3]]; (*1=Oncurve 0=Offcurve*)
len = Count[ptb, 1] - 1;
n = IntegerPart[(len ) t] + 1;
n = (Position[ptb, 1] // Flatten)[[n]];
t1 = len Mod[t, 1/len];
If[ptb[[n + 1]] == 0,
(*
r=BSplineFunction[pta[[n;;n+2]],SplineDegree->2,SplineClosed->
False][t1];
*)
r = BezierFunction[pta[[n ;; n + 2]], SplineDegree -> 2][t1];
,
r = {
pta[[n, 1]] + (pta[[n + 1, 1]] - pta[[n, 1]]) t1,
pta[[n, 2]] + (pta[[n + 1, 2]] - pta[[n, 2]]) t1
};
];
ret = Append[ret, r];
i = i + 1;
];
Return[ret];
];
先ほど変換したTrueType Fontを読み込みます。
pts = Import["a.m"];
TrueTypeを変換するのがめんどーな方は、下記コードを入力してください。
pts = {{{1180, 977, 1}, {1160, 1040, 0}, {1110, 1077, 1}, {1143,
1114, 1}, {1233, 1076, 0}, {1290, 975, 1}, {1522, 948, 0}, {1660,
829, 1}, {1804, 704, 0}, {1804, 502, 1}, {1804, 227, 0}, {1523, 72,
1}, {1333, -33, 0}, {1053, -66, 1}, {1036, -8, 1}, {1375, 72,
0}, {1528, 210, 1}, {1669, 337, 0}, {1669, 524, 1}, {1669, 688,
0}, {1540, 796, 1}, {1441, 879, 0}, {1294, 905, 1}, {1276, 804,
0}, {1170, 641, 1}, {1040, 459, 0}, {901, 340, 1}, {911, 290,
0}, {930, 250, 1}, {954, 186, 0}, {954, 168, 1}, {954, 80,
0}, {895, 80, 1}, {847, 80, 0}, {805, 258, 1}, {569, 70, 0}, {414,
70, 1}, {252, 70, 0}, {252, 254, 1}, {252, 461, 0}, {427, 648,
1}, {565, 795, 0}, {766, 885, 1}, {771, 973, 0}, {784, 1151,
1}, {721, 1147, 0}, {647, 1147, 1}, {518, 1147, 0}, {451, 1187,
1}, {393, 1221, 0}, {356, 1298, 1}, {404, 1333, 1}, {466, 1237,
0}, {627, 1237, 1}, {706, 1237, 0}, {795, 1247, 1}, {816, 1421,
0}, {816, 1466, 1}, {816, 1502, 0}, {789, 1524, 1}, {766, 1544,
0}, {701, 1573, 1}, {723, 1620, 1}, {963, 1588, 0}, {963, 1503,
1}, {963, 1476, 0}, {940, 1425, 1}, {919, 1386, 0}, {899, 1260,
1}, {1025, 1281, 0}, {1186, 1337, 1}, {1215, 1346, 0}, {1252, 1370,
1}, {1290, 1397, 0}, {1358, 1397, 1}, {1438, 1397, 0}, {1438,
1346, 1}, {1438, 1307, 0}, {1399, 1290, 1}, {1205, 1218, 0}, {885,
1167, 1}, {869, 1061, 0}, {862, 920, 1}, {1002, 969, 0}}, {{1184,
909, 1}, {1025, 900, 0}, {858, 840, 1}, {847, 638, 0}, {879, 430,
1}, {994, 550, 0}, {1110, 735, 1}, {1172, 826, 0}}, {{787, 352,
1}, {761, 541, 0}, {764, 801, 1}, {599, 717, 0}, {482, 566,
1}, {367, 418, 0}, {367, 274, 1}, {367, 176, 0}, {461, 176,
1}, {507, 176, 0}, {603, 228, 1}, {696, 278, 0}}};
最後に下記コマンドで「あ」がプロットされます。
ParametricPlot[Gryph2[pts, t], {t, 0, 1}]
8. Mathematicaを買いにでかけよう!
Q.「Mathematicaって何処で売っているの?」A.「新宿のヨドバシ・カメラや、秋葉原Laoxのザ・コンピュータ館や、神保町の書泉で売って・・・」ましたが、今は手に取れるパッケージ版の扱いはない様です。私はLaoxのザ・コンピュータ館でお金を貯めて入社4年目くらいに買いました。代理店は株式会社ヒューリンクス ( HULINKS Inc. )で今でもお世話になっています。Wolfram Researchの国内認定販売代理店は、2016年5月14日現在下記があるようです。
- HULINKS Inc.
- Japan Information Processing Service Co Ltd
- Ryoka Systems Inc
私は一般企業所属なので割り引き価格とかお店のポイント還元くらいでしたが、代理店ですと官庁や教育関連は交渉の余地があるみたいですね。まぁMathematicaのホーム・エディションくらい扱ってくれるお店が有っても良いんぢゃないかなぁって思います。イキナリ代理店とやり取りするとか、ビジネスマナーを覚えないとキツイですよねぇ。そーいう意味ではラズベリーパイ用のMathematicaは手軽に紹介が出来て便利ですねw ラズベリーパイは秋葉原で4000円くらいで買えます。Mathematicaをゲットする為に先ずはお試しにラズパイを買いにでかけましょうw ラズパイの使い方はQiitaで検索すれば色々と丁寧な記事が見つかります。便利になりましたね。所で、「いかにして問題をとくか : G. ポリア, G. Polya, 柿内 賢信訳」の序文にラズベリーパイは食べてみないと味が分からないという記述があるのですが、ワンボードマイコンのラズパイの語源と関連があるんですかね。どなたかご存じないですか?
Twitterで教えて頂きました。
we wanted a fruit name for nostalgic reasons, and the Pi comes from Python.
(日本語訳)私たちはノスタルジックな理由により、果物の名前を付けたかった。そして、「Pi」は「(プログラミング言語の)Python」に由来している。
via:「The name 'Raspberry Pi'」・Raspberry Pi
Twitter "ラズベリーは過去のマイコンデバイスにフルーツの名前をつけたものが多かったことに由来し、Piはプログラミング言語のPythonから取っていたはずです。"
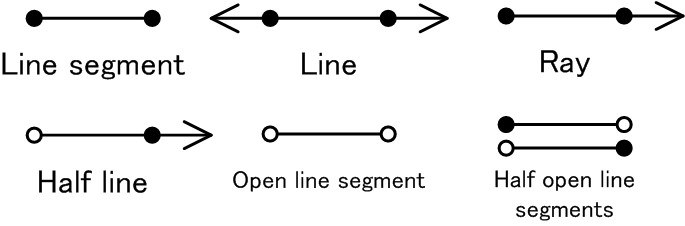
9. 半直線と半直線
Mathematicaでは半直線を表すオブジェクトが2つあります。HalfLineとRayです。どちらも半直線なのでHalfLineで良いと思うのですが、なぜかMathematicaにはRayもあります。なんでそうなのぉ?
開区間、閉区間について、Mathematicaは閉区間をIntervalオブジェクトであらわします。共通集合∩と和集合∪は、IntervalIntersectionとIntervalUnionで区間演算ができます。またIntervalは幾何学領域として扱う事ができます。ところが幾何学領域ですと、それは線分Lineでも出来て、RegionIntersectionとRegionUnionで区間演算できます。ちょっとヤヤコシイですし、開区間の扱い方がワカラナイですね。気をつけましょう。
下記にMathematicaと英語と日本語の直線に関する語句を勝手にまとめてみました。あくまで参考です。インターネットでざっと調べてみたところ半直線は現在(2016年5月23日時点)のところ縁を含んでいると思われますが、もしかしたら将来、数学の気が変わって、縁を含まなくなったりするかもしれません。
| Mathematica | English | 日本語 | 説明 |
|---|---|---|---|
| Line | Line segment | 線分 | 両端を持つ直線 |
| InfiniteLine | Line | 直線 | 両端を持たない直線 |
| HalfLine | Ray(or Half-Line) | 半直線(縁を含む) | 閉じた一端を持つ直線 |
| Ray | Ray(or Half-Line) | 半直線(縁を含む) | ボロノイ図の開いた多角形を表すのに使われる. |
| なし | Ray | 半直線(縁を含む) | 閉じた一端を持つ直線 |
| なし | Half-Line | 半直線(縁を含まない) | 開いた一端を持つ直線 |
| なし | Open line segment | 縁を含まない線分 | 開いた両端を持つ線分 |
| なし | Half open line segment | どちらか1つの縁を含まない線分 | 閉じた一端を持つ線分 |
10. ビットとビット
”通信の意味論的側面が工学的側面に対して当てはまらない” Claude E.Shannon
ビットとビットの意味について。切っ掛けは下記ツイートです。
Twitter "🔖 “解凍”と呼ぶのはおっさんだけ? 某社さんの高校「情報」教科書(旧版)を貼っておく(ちなみにこの「圧縮」の定義も酷い)
まず圧縮と解凍についてですが、MathematicaではCompressを圧縮する、Uncompressを解凍する、と説明しています。
次にビットという単位について、ビットは情報理論では情報量の単位として特別な意味を持ちます。一方で普通は、このOSは64ビットですとか処理する情報の単位を表したり、ハードディスクの容量が1テラ・バイトですとか、半導体メモリの容量が32キロ・バイトなど情報の大きさの単位を表したりするのに使用されます。8ビットは1バイトを表します。
圧縮の定義について、例えば”A,A,A,A,A,A,A,A”という同じ情報が並んでいる場合、それらを記憶するには8個の領域が必要です。
In[11297]:= ByteCount["AAAAAAAA"]
Out[11297]= 40
これをAが8個という表現にすれば、冗長性を利用した圧縮ができます。
StringRepeat["A",8]
これはロスレス圧縮の一例ですが、このように情報を減らすことを圧縮といいます。
情報の圧縮は工学的には重要で、例えばMP3プレイヤーなど携帯型音楽プレイヤーには圧縮の技術は欠かすことができません。
ここで情報について、シャノンが警告的な言葉を残しているので引用してみます。
この通信の理論における情報(information)という言葉は特別な意味に使われ、普通の使い方と混同してはならない。とくに情報は、意味と混同してはならない。
事実2つのメッセージがあり、その1つは多くの意味をにない、もう1つは全く無意味な場合、情報について言えば、問題の観点からは、この2つのメッセージは厳密に等価であり得る。シャノンが”通信の意味論的側面が工学的側面に対して当てはまらない”と言うときに意味するものは、正にこのことである。コミュニケーションの数学的理論P16より引用
情報科の人が情報を特別な意味に用いるのは構わないと思いマスシ、私も不勉強ながらも確認したり勉強しながら理解しようと努めています。
ところで、
In[11313]:= ByteCount["A"]
ByteCount["AA"]
ByteCount["AAA"]
ByteCount["AAAA"]
ByteCount["AAAAA"]
ByteCount["AAAAAA"]
ByteCount["AAAAAAA"]
ByteCount["AAAAAAAA"]
Out[11313]= 32
Out[11314]= 32
Out[11315]= 32
Out[11316]= 32
Out[11317]= 32
Out[11318]= 32
Out[11319]= 32
Out[11320]= 40
MathematicaはAが1個から7個で32バイト、Aが8個で40バイトの領域を必要とします。教科書通りではないので気をつけましょう。
11. 固定小数点表示
関数電卓には、小数第n位まで求める固定小数点演算モードがあります。
Mathematicaでこれをやるのは少々面倒です。まず、小数第n+1位を(本当に)四捨五入して、小数第n位まで求める関数を作ってみます。
(*有効桁付き出力 *)
Unprotect[Fix];
Clear["Global`*"];
Fix[an_, ad_] := Module[{ret, n, d},
n = ToExpression[
StringSplit[ToString[FullForm[Abs[an]]], "`"][[1]] <>
If[
Length[
StringPosition[ToString[FullForm[Abs[an]]], "^"]
] == 0,
"",
"*10^" <> StringSplit[ToString[FullForm[Abs[an]]], "^"][[2]]
]
];
d = ad;
If[d <= 0, Return[0]];
ret = N[
If[ 10 (n/d - Floor[n/d]) >= 5, Ceiling[n/d] d, Floor[n/d] d]
,
If[d < 1,
Length[IntegerDigits[Floor[n/d]]],
Length[IntegerDigits[Floor[n]]]
]
];
If[an < 0, ret = -1 ret];
Return[ret];
];
Protect[Fix];
例えば、10/3を小数第2位まで求めるには、下記の様にします。
In[7826]:= Fix[10/3, 1/100]
Out[7826]= 3.33
次に10 000 000 /3を小数第2位まで求めてみます。
In[7832]:= Fix[10000000/3, 1/100]
Out[7832]= 3.33333333*10^6
桁が9桁を超えると科学表記になってしまいます。なんで、そうなのぉ?
これは、会計用表記で防ぐ事ができます。
In[7833]:= Fix[10000000/3, 1/100] // AccountingForm
Out[7833]//AccountingForm= 3333333.33
ただ負の数の-6.7が(6.7)と表示されてしまうので注意が必要です。
11.1 NumberForm
NumberFormを使って小数第2位まで表示してみます。
In[1]:=NumberForm[0.995, 2]
Out[1]//NumberForm=0.99
なんでそうなの~?0.995は末尾5が繰り上がって1になる・・・と思うのですが、最近自信がなくなってきました。
で、0から10までの数値に0.995を足して小数第2位に丸めてみますと、
In[2]:=NumberForm[Table[n + 0.995, {n, 0, 10}],{Infinity,2}]
Out[2]//NumberForm={0.99,2.00,3.00,4.00,5.00,6.00,7.00,8.00,8.99,9.99,11.00}
0と8と9で繰り上がりが発生しないようです。
Wikipediaの四捨五入によりますと、
- 数値が実際より増えると誇張・虚偽・捏造・難解と見なされる恐れがあるときは、切り捨てられる。
とありますので、0,8,9辺りで何か事情があるのでしょうか。
12. リサージュ曲線
二つの正弦波形の振幅と周波数と位相を比較する時にリサージュ曲線を使うと一目瞭然で便利です。昔は電子発振器の周波数を測る時に、各定数が既知の正弦波と未知の正弦波でリサージュ波形をオシロスコープで描いて測定していたそうです。周波数の測定は今では周波数カウンタを使います。
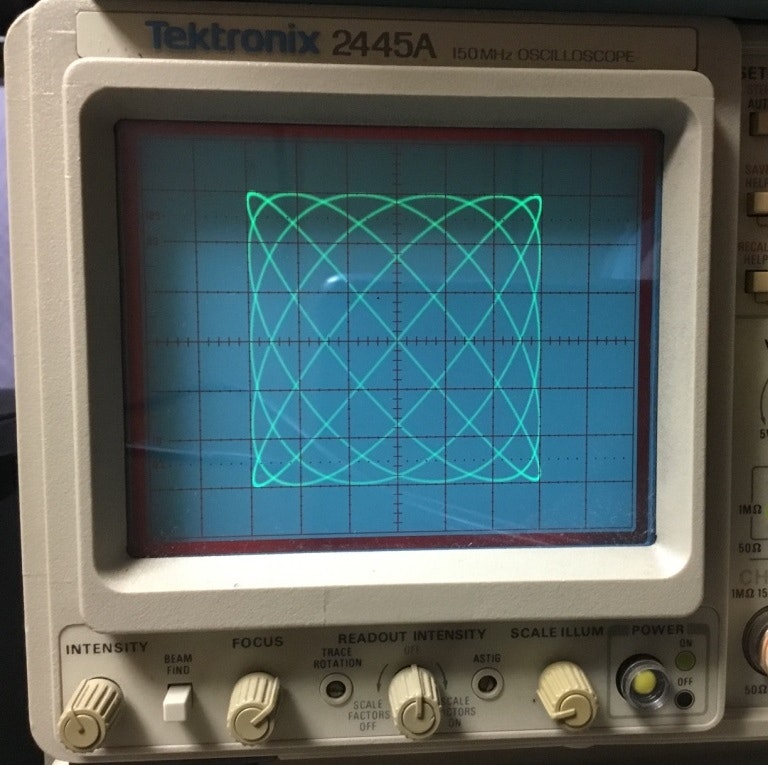
もちろんMathematicaでもリサージュ曲線を描く事ができます。
In[1]:= ParametricPlot[{Sin[2π 5 t], Sin[2π 6 t]}, {t, 0, 1}]
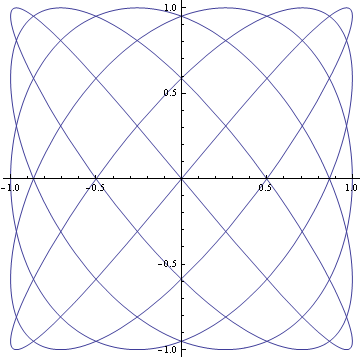
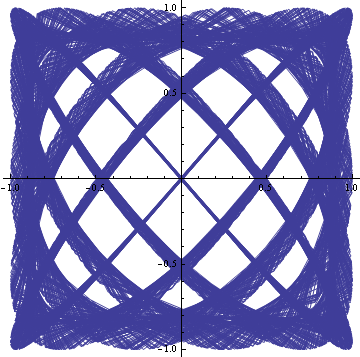
ところで、リサージュ曲線は静止しているハズなので、プロット範囲のtを1から100くらいに増やしても変化しないハズです。
In[2]:= ParametricPlot[{Sin[2π 5 t], Sin[2π 6 t]}, {t, 0, 100}]
これはプロット範囲が増えてサンプル点が不足した為、標本化誤差が発生したと考えられます。
PlotPointオプションを10,000位に設定すると良いです。但し少し時間がかかります。
In[3]:= ParametricPlot[{Sin[2π 5 t], Sin[2π 6 t]}, {t, 0, 100},
PlotPoints -> 10000]
周期の長い組み合わせでリサージュ曲線を描くときは気をつけましょう。
12.1 グリッド
オシロスコープと同じ感じでプロットにもグリッドが入ると比較がし易いです。下記の様にすれば同じ感じになります。
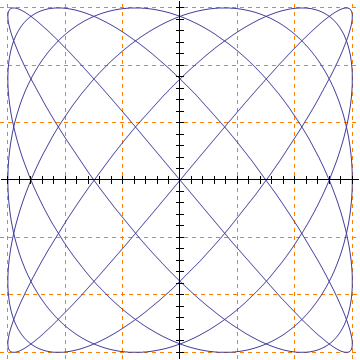
In[4]:= ParametricPlot[{Sin[2 \[Pi] 5 t], Sin[2 \[Pi] 6 t]}, {t, 0, 1},
Ticks -> {{#, "", {1, 1} 1/100} & /@ (Range[-15, +15]/15), {#,
"", {1, 1} 1/100} & /@ (Range[-15, +15]/15)},
GridLines -> {Range[-3, +3]/3, Range[-3, 3]/3},
GridLinesStyle -> Directive[Orange, Dashed]]
13. 補数
10進数を2進数に変換するには、BaseFormを使います。
\begin{align}
In[1]:&= BaseForm[6,2] \\
Out[1]&= 110_2
\end{align}
2進数を10進数に変換するには、^^を使います。
\begin{align}
In[2]:&= 2 \verb|^|\verb|^| 110 \\
Out[2]&= 6
\end{align}
2進数110の各桁のNOTを取ってみます。
\begin{align}
In[3]:&= BitNot[ 2 \verb|^|\verb|^| 110] \\
Out[3]&= -7
\end{align}
なんで、110のNOTは001にならないのぉ~?
IntegerDigitsで桁数字をリスト形式にすると確かに111になってしまっています。
\begin{align}
In[4]:&= IntegerDigits[ BitNot[ 2 \verb|^|\verb|^| 110] ,2] \\
Out[4]&= \{ 1,1,1 \}
\end{align}
そこで、下記の様にBitAndを用いて、下位3bitだけを返す様にしてみます。
\begin{align}
In[5]:&= IntegerDigits[ BitAnd[BitNot[ 2 \verb|^|\verb|^| 110],2 \verb|^|\verb|^| 0111] ,2] \\
Out[5]&= \{ 1 \}
\end{align}
110のNOTは001なので1が返ります。
Mathematicaは110をNOTすると上位の桁に続く見えない0もNOTし、・・・0000 0110を・・・1111 1001とし、それを2の補数表記で-7と返します。よってBitNotは、
BitNot[n\verb|_|]:=-1-n;
という数式と等価で、n=6ならば、BitNot[6]=-7となります。コンピュータの有限長なレジスタに対するNOT演算と違いますよね。気をつけましょう。
14.評価して!
Mathematicaで下記の問題を解いてみます。
ある野球選手は5回に2回の割合でヒットを打つという。この選手が2試合で8回打席に立ったとき、ヒットを打つ本数をXとし、次の問いに答えよ。ただし、各回のヒットはすべて独立であるとする。
(1) Xの確率分布を求めよ。
| 本数 X | 1 | 2 | 4 | 6 |
|---|---|---|---|---|
| 確率 P | ア | イ | ウ | エ |
| (小数第3位まで) |
第78回計算技術検定1級3統計処理 (3)より
簡単な二項分布の問題ですね♪ 計算すると、
In[1]:= Table[PDF[BinomialDistribution[8, 2/5], n], {n, {1, 2, 4, 6}}] //
Limit[Round[# + n, 1/1000], n -> 0, Direction -> "FromAbove"] & // N
Out[1]= {0.09, 0.209, 0.232, 0.041}
アが0.090、イが0.209、ウが0.232、エが0.041と求まりました。
趣味で問題を解いていると、ヒットを0本から8本打つ確率をグラフで見たいなぁと思いますよね?
In[2]:= Plot[PDF[BinomialDistribution[8, 2/5], x], {x, 0, 8}, Filling -> Axis]
・・・なんでそうなのぉ?
確率密度関数(PDF)や微分方程式の解などの方程式をPlotするときはEvaluateを入れないとPlot関数で評価を実行して数値にしてグラフにしてくれないのです。。。なので、
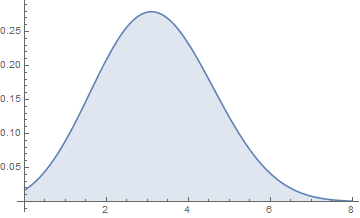
In[2]:= Plot[PDF[BinomialDistribution[8, 2/5], x]// Evaluate, {x, 0, 8}, Filling -> Axis]
と綺麗なグラフを描いてくれます。8打席全部ヒットを打つ確率がスゴク小さい事がわかって便利ですね。ちなみに確率Pを計算すると0.00065536になります。
14.1 順列nPr
確率といえば、階乗と順列と組み合わせですが、Mathematicaでは順列nPrを求める関数が見当たりません。なので順列nPrは、私の場合、二項係数にr!を乗じて求めています。
In[2]:= n! (* nの階乗 *)
Binomial[n,r] r! (* nPr 順列 *)
Binomial[n,r] (* nCr 組み合わせ *)
なんでMathematicaには順列の計算(n!/(n-r)!)がないのだろう?
15.Raspberry PiでMathematicaが動かない!
Raspberry Piの公式OSであるRaspbianをインストールするとMathematicaが入っています。そこで起動してみると・・・
Activation Keyを聞かれてしまいました!RASPBERRY PI用Wolfram言語とMathematicaは無料なのに、(2018年12月3日現在)
なんでそうなのぉ~。
調べてみると、ライセンスはプリインストールされているが、ラズパイのビデオ・コアにアクセスするために、video(/dev/vhiq)とwww-dataのアクセス権が必要なようです。そこでユーザーをvideoとwww-dataの補助グループへ追加します。
$ sudo usermod -a -G video,www-data [ユーザ名]
$ logout
ユーザを補助グループに追加して再ログインすれば起動するようになります。
ちなみにVersionは11.3.0です(2018年12月3日現在)。最新ですね♪感謝です。
$ wolfram
Wolfram Language 11.3.0 Engine for Linux ARM (32-bit)
Copyright 1988-2018 Wolfram Research, Inc.
In[1]:= $Version
Out[1]= 11.3.0 for Linux ARM (32-bit) (May 23, 2018)
In[2]:= Quit
$
参考Can't run Mathematica on Raspberry Pi under php
15.1 Raspbian Buster
ラズパイのOSであるRaspbianのBusterをダウンロードしてきたらMathematicaが入っていませんでした。なんでそうなのぉ~。
Busterとの互換性で一時的に削除されたとの事です。下記コマンドでインストールしましょう。
$ sudo apt install wolfram-engine
$ wolfram
Mathematica 12.0.1 Kernel for Linux ARM (32-bit)
Copyright 1988-2019 Wolfram Research, Inc.
In[1]:= $Version
Out[1]= 12.0.1 for Linux ARM (32-bit) (June 23, 2019)
In[2]:= Quit
$
参考Raspbian 2019-06-20 Release-note 翻訳
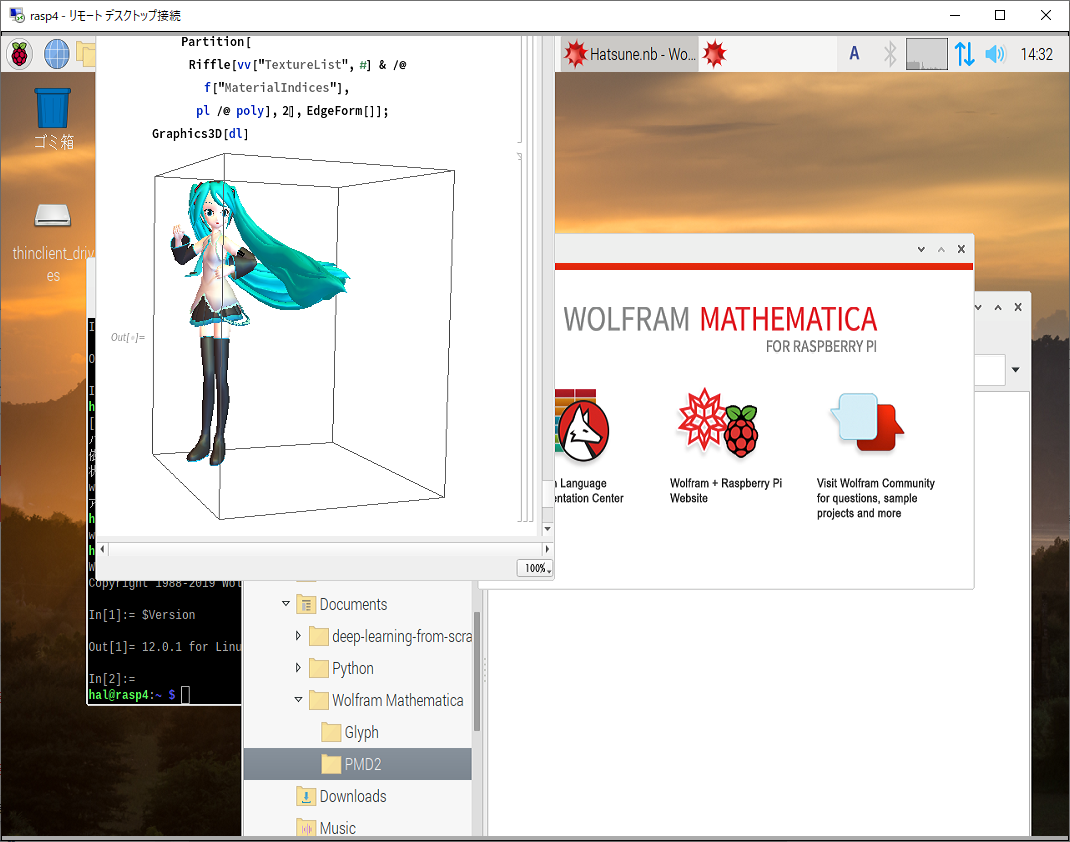
15.2 ラズパイの窓が画面外
PCのノートブックをラズパイに持ってきて開くとたまにタイトルバーが画面外に出てしまい窓が移動できません。なんでそうなのぉ~。
移動したい窓の中にマウスカーソルを入れてから、ALTキー押しつつマウスの左ボタンを押しながらドラグすると窓を移動できます。
15.3 Windowsの窓で画面外
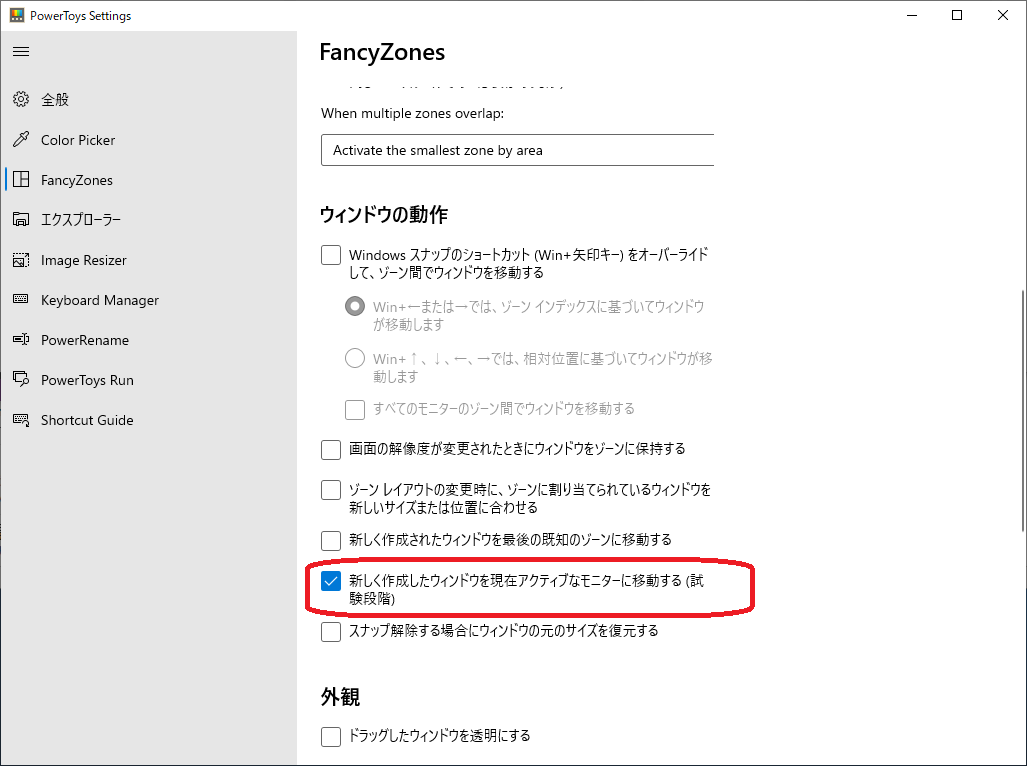
PCのノートブックでも最近、Mathematicaのノートブックがたま~に画面外になることがあります。再現条件が分からないのですが、Microsoft PowerToyの設定で防げそうです。
FancyZonesの項目の「新しく作成したウィンドウを現在アクティブなモニターに移動する(試験段階)」にチェックを付ける。
なんとなく、セミナーで頂いたノートブックを開いていじっている時に気が付くと新規ウィンドウが画面外に開くような。。。
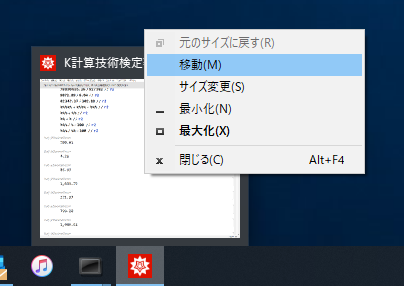
15.4 Windowsの窓で画面外2
Windowsの下端のタスクバーのMathematicaアイコンにマウス・カーソルを合わせると上にプレビューが表示されます。マウス・カーソルをそのままプレビューに合わせた後に右クリック→移動(M)にマウス・カーソルを合わせてマウスを左クリックします。(下画面参照) 次にキーボード・カーソルキーの↑キーを押下してから、マウスを左右に動かして画面内に窓を移動できたらマウスを左クリックで確定します。
16. 添え字の置換
Mathematicaでは「CTRL+マイナス」キーで右下へ添え字を付けられます。しかし置換を使うと、
\begin{align}
In[1]:&= v + R_v /. v->10 \\
Out[1]&=10 + R_{10}
\end{align}
と、このように添え字のvも10へ置換されます。なんでそうなのぉ~~~。
RvはそのままRvにしておいて~(涙)。気をつけましょう。というより、添え字使わない方が良いかも?
17. 第138回 珠算電卓検定 ビジネス計算1級を解いてみた。
Mathematica便利ですよね?今回は「なんでそうなの~?」ネタは無いと思うのですが、珠算電卓検定のビジネス計算1級の共通問題を解いてみます。選択問題は私には難しいので、どなたか解説して頂ければ助かります。。。
第142回から解式を公開していただけるようになりました♪(2021.12.27追記)
17.1 初期化
ご破算をして、円未満四捨五入の関数r0と、ドルとユーロのセント未満四捨五入の関数r2を定義します。
Clear["Global'*"];
r2[x_, y_ : 2] := AccountingForm[N[Round[x, 1/100]], {Infinity, y}, DigitBlock ->3];(* $ € *)
r0[x_, y_ : 0] := AccountingForm[N[Round[x, 1/100]], {Infinity, y}, DigitBlock -> 3];(* ¥ *)
17.2 ビジネス計算1級 共通問題
(1)額面¥605,000の約束手形を割引率年2.15%で8月16日に割り
引くと,割引料はいくらか。ただし,満期は10月8日とする。
(両端入れ,円未満切り捨て)
605000(2.15/100(DayCount[{1, 8, 16}, {1, 10, 8}] + 1)/365) //Floor//r0
DayCountは片端入れなので+1をします。Floorで切り捨てです。
(2)¥8,230,000を年利率3.1%の単利で1年3か月間貸し付けた。元利
合計はいくらか。(円未満切り捨て)
8230000 (1 + 3.1/100 (1 + 3/12)) // Floor // r0
(3)¥3,780,000を年利率7%,半年1期の複利で4年6か月間借り入れる
と,複利終価はいくらか。(円未満4捨5入)
3780000 (1 + 7/2/100)^(2 (4 + 1/2)) // r0
半年1期なので年利率を2で割って、期間は2倍します。結果は¥5,151,752-になります。複利こわい。
(4)100米トンにつき$51,200の商品を50kg建にすると円でいくらか。
ただし,1米トン=907.2kg,$1=¥109.60とする。
(計算の最終で円未満4捨5入)
51200/100 1/907.2 50 109.60 // r0
米トンはヤード・ポンド法で2,000ポンドなので907.185kgですので15gの差がありますが、取り決め次第でしょうか。
(5)取得価額¥750,000 耐用年数19年の固定資産を定率法で減価償却
すれば,第4期首帳簿価額はいくらになるか。ただし,決算は年1回,
残存簿価¥1とする。(毎期償却限度額の円未満切り捨て)
f[0] := 750000; f[n_] := f[n - 1] - Floor[f[n - 1] 0.105];
f[4 - 1] // r0
残存簿価が式に関係してないのが立式時に気になりました。定率法償却率は数表から引き19年で.105です。再帰関数での計算に行きつくまで結構試行錯誤しました。第4期の期首なので第3期の期末と考えてf[4-1]としました。まだ吟味が足りてないとは自分も思います。
(6)7月11日満期,額面¥9,500,000の手形を割引率年4.05%で5月7日
に割り引くと,手取金はいくらか。(両端入れ,割引料の円未満切り捨て)
x-Floor[x 4.05/100 (DayCount[{1, 5, 7}, {1, 7, 11}] + 1)/365] /.x->9500000 // r0
DayCount便利ですね。31-7+30+11=65とかの計算よりも分かりやすいです。平年とうるう年に注意が必要ですが。両端入れなので+1します。
(7)ある商品を定価から値引きして¥5,740,800で販売したところ,原価
の10.4%の利益となった。原価の38%の利益を見込んで定価をつけてい
たとすれば,値引額は定価の何パーセントであったか。
y/.Solve[(x(1+104/10/100)==b&&(x(1+38/100))(1-y/100)==b)/.b->5740800,{x,y}][[1]]// r0
xが原価、yは値引額の定価に対するパーセンテージです。10.4%でSolveすると例の警告が出るので、104/10としています。初心者の頃にSolveの結果を利用する方法に結構悩みました。
(8)元金¥4,380,000を年利率1.4%の単利で借り入れたところ,元利
合計¥4,397,136を支払った。借入期間は何日間であったか。
x/.Solve[4380000(1+1.4/100 x/365) == 4397136, x][[1]]
答えは整数になりました。というか借入期間が整数の0から365までの全てで整数になりますね。作問者の数字選びに工夫を感じました。この検証にはAllTrue関数を使いました。
(9)7年後に支払う負債¥6,870,000を年利率6%,1年1期の複利で割り
引いて,いま支払うとすればその金額はいくらか。(¥100未満切り上げ)
Ceiling[x /. Solve[ x (1 + 6/100)^7 == 6870000, x][[1]], 100] // r0
切り上げにはCeilingを使います。
(10)翌年1月28日満期,額面¥792, 650の手形を11月14日に割引率
年3.45%で割り引くと,手取金はいくらか。ただし,手形金額の¥100
未満には割引料を計算しないものとする。
(両端入れ,割引料の円未満切り捨て)
(x-Floor[Floor[x,100] 3.45/100 ( DayCount[{1, 11, 14}, {2,1,28}]+1)/365])/. x ->792650 // r0
切り捨てにはFloorを使います。
(11)仲立人が売り主から2.9%,買い主から2.7%の手数料を受け取る
約束で商品の売買を仲介したところ,仲立人の手数料合計が¥358,400
となった。売り主の手取金はいくらか。
x(1-2.9/100) /. Solve[-x (1 - 2.9/100) + x (1 + 2.7/100) == 358400, x][[1]] // r0
xは商品の値段です。Solveの中で仲立人(なかだちにん)の立場で方程式を立てて、式の始めで売主の手取り金を計算しています。
(12)次の3口の借入金の利息を積数法によって計算すると,利息合計は
いくらになるか。ただし,いずれも期日は5月13日,利率は年0. 7%
とする。(平年,片落とし,円未満切り捨て)
借入金額 借入日 ¥5,400,000 2月15日 ¥2,800,000 3月23日 ¥1,900,000 4月 5日
{5400000 (0.7/100 (DayCount[{1, 2, 15}, {1, 5, 13}] + 0)/365),
2800000 (0.7/100 (DayCount[{1, 3, 23}, {1, 5, 13}] + 0)/365),
1900000 (0.7/100 (DayCount[{1, 4, 5}, {1, 5, 13}] + 0)/365)}
//Total //Floor //r0
各利息で円未満切り捨てちゃうと答えが違ってきます。計算最後で切り捨てなんですね。
(13)¥420,000を年利率5.5%,1年1期の複利で12年6か月間貸し付け
ると,期日に受け取る元利合計はいくらになるか。ただし,端数期間は単
利法による。(計算の最終で円未満4捨5入)
420000 (1 + 5.5/100)^12 (1 + 5.5/100 1/2) // r0
(14)4kgにつき¥6,200の商品を3,600kg仕入れ,諸掛り¥270, 000
を支払った。この商品に諸掛込原価の4割4分の利益を見込んで定価を
つけたが,全体の$\frac{2}{3}$は定価から1割8分引きで販売し,残り全部は
定価から¥702,600値引きして販売した。総売上高はいくらか。
2/3 x (1-1.8/10)+1/3 x -702600 /. x -> (6200/4 3600 + 270000) (1 + 4.4/10) // r0
xは仕入れた商品の諸掛り+商品価格です。定価から1割8分引きは良いとして、¥702,600値引きの意味の読み取りで1商品の販売価格からの値引きと勘違いしたりして立式にてこずりました。ビジネス計算は共通問題と選択問題合わせて30分で解くとの指示があるのですが、もし本当に資格試験を受験するのなら見直す時間キツイですぅ。(私は受験したことないです。)
(15)取得価額¥8,940,000 耐用年数32年の固定資産を定額法で減価償却
するとき,次の減価償却計算表の第4期末まで記入せよ。ただし,決算は
年1回,残存簿価¥1とする。
期数 期首帳簿価額 償却限度額 減価償却累計額 1 2 3 4
8940000 {1, 0.032, 0.032}
{%[[1]] - %[[2]], %[[2]] , %[[2]] + %[[3]] } // r0
{%[[1]] - %[[2]], %[[2]] , %[[2]] + %[[3]] } // r0
{%[[1]] - %[[2]], %[[2]] , %[[2]] + %[[3]] } // r0
計算式的には、同一リスト中の手前の列の結果を取得したい( {a,b,c,ここで一つ前のcを指す方法} ) があると便利なのですが、わからないので%で一つ前の式から再計算する方針で立式しました。
17.3 解いてみての感想など
四捨五入にRoundを使っても答えが合っています。数字を選んでるんですかね。。。
原価償却問題や、選択問題の【複利年金の計算】、【証券投資の計算】、【経営分析の計算】についても、問題文を読んでMathematicaで立式できれば良いなぁと年に1回問題を趣味で解いています。皆さんもいかがですか。
18.並列足し算
Mathematicaで下記の問題を解いてみます。
1から9までの数が1つずつ書いてあるカードが9枚ある。この中から同時に2枚のカードを抜きだし、大きい数をXとする。次の問いに答えよ。
(1)X=6となる確率を求めよ。(小数第4位まで)
(2)大きい数の期待値E(X)を求めよ。(少数第1位まで)第83回計算技術検定1級3統計処理 (3)より
簡単な順列組合せの問題ですね♪ 計算すると、
In[1]:= Clear["Global`*"];
f[x_, y_ : 2] := NumberForm[x, {Infinity, y}];
p[n_, k_] := n!/(n - k)!;
c[n_, k_] := p[n, k]/k!;
5/c[9, 2] // N // f[#, 4] &
(Table[n, {n, 1, 9}] . {0, 1, 2, 3, 4, 5, 6, 7, 8})/c[9, 2] // N //
f[#, 1] &
Out[5]//NumberForm= 0.1389
Out[6]//NumberForm= 6.7
1)X=6となる確率が0.1389
2)大きい数の期待値E(X)が6.7
と求まりました。
MathematicaにはPermutationsという関数があります。ので、これを使って計算すると、
Clear["Global`*"];
f[x_, y_ : 2] := NumberForm[x, {Infinity, y}];
Map[Sort[#, Greater] &, Permutations[Table[n, {n, 1, 9}], {2}]];
DeleteDuplicatesBy[%, # . {x, y} &]
Select[%, #[[1]] == 6 &]
Length[%]/Length[%%] // N // f[#, 4] &
Map[#[[1]] &, %%%]
Mean[%] // N // f[#, 1] &
で、結果は
Out[340]=
{{2, 1}, {3, 1}, {4, 1}, {5, 1}, {6, 1}, {7, 1}, {8, 1}, {9, 1}, {3,
2}, {4, 2}, {5, 2}, {6, 2}, {7, 2}, {8, 2}, {9, 2}, {4, 3}, {5,
3}, {6, 3}, {7, 3}, {8, 3}, {9, 3}, {5, 4}, {6, 4}, {7, 4}, {8,
4}, {9, 4}, {6, 5}, {7, 5}, {8, 5}, {9, 5}, {7, 6}, {8, 6}, {9,
6}, {8, 7}, {9, 7}, {9, 8}}
Out[341]=
{{6, 1}, {6, 2}, {6, 3}, {6, 4}, {6, 5}}
Out[342]//NumberForm=0.1389
Out[343]=
{2, 3, 4, 5, 6, 7, 8, 9, 3, 4, 5, 6, 7, 8, 9, 4, 5, 6, 7, 8, 9, 5, 6, \
7, 8, 9, 6, 7, 8, 9, 7, 8, 9, 8, 9, 9}
Out[344]//NumberForm=6.7
と答えが返ってきます。リストで実際のカードの順列を出して、数え上げる計算の方が分かりやすいですね。ところで、DeleteDuplicatesByで内積を使って重複を削除したのですが、他に良い方法ありますかね。これで便利にできるので思いがけないところでリスト処理に内積を使ってしまいます。
18.1 実際に乱数でカードを取り出して計算してみる。
2枚のカードを乱数で抜き出して、大きい順にならべるモジュールrcを書いてみます。
rc[table_] := Module[
{t = table, rc1, t1, rc2, ret},
rc1 = RandomChoice[t];
t1 = Drop[t, {rc1}];
rc2 = RandomChoice[t1];
ret = Sort[{rc1, rc2}, Greater];
Return[ret];
];
rc[Table[n, {n, 1, 9}]]
とすると、
Out[353]= {8, 4}
と2枚のカードをランダムに抜き出して大きい順に並べて返してきます。
次に、大きい数が8だったら、長さ9のリストの8番目を1にするテーブルを作成します。
Table[Switch[%[[1]] == n, True, 1, False, 0], {n, 1, 9}]
Out[354]={0, 0, 0, 0, 0, 0, 0, 1, 0}
これを普通にFor分で10万回ほど試行してみると。
t = Table[0, {n, 1, 9}]
For[i = 0, i < 100000, i = i + 1,
t = t +
Table[Switch[rc[Table[n, {n, 1, 9}]][[1]] == n, True, 1, False,
0], {n, 1, 9}];
] // Timing
t
t[[6]]/Total[t] // N // f[#, 4] &
Total[t . Table[n, {n, 1, 9}]]/Total[t] // N // f[#, 1] &
Out[387]={0, 0, 0, 0, 0, 0, 0, 0, 0}
Out[388]={9.5, Null}
Out[389]={0, 2781, 5485, 8408, 11259, 13996, 16604, 19580, 22048}
Out[390]//NumberForm=0.1397
Out[391]//NumberForm=6.7
と答えが返ってきますが約10秒ほど掛かります。。。また乱数を使ってるので計算結果は順列・組合せと微妙に違いますが、試行回数を増やせば小数第4位までくらいなら同じになるはず!
18.1.2 ParallelSumを使ってみる
というわけで、やっと本題ですが、ここで並列加算を使って同じ計算をしてみます。
ParallelSum[
Table[Switch[rc[Table[n, {n, 1, 9}]][[1]] == n, True, 1, False,
0], {n, 1, 9}], {i, 1, 100000}] // Timing
t = %[[2]];
t[[6]]/Total[t] // N // f[#, 4] &
Total[t . Table[n, {n, 1, 9}]]/Total[t] // N // f[#, 1] &
Out[392]={0.21875, {0, 2729, 5490, 8311, 11102, 13986, 16699, 19501, 22417}}
Out[394]//NumberForm=0.1395
Out[395]//NumberForm=6.7
と約0.2秒ほどで答えが返ってきます♪ 速いので試行回数を10万回から100万回に増やして1.4秒、1千万回で17.4秒ですが体感1分くらい(?)で答えが返ってきます。X=6となる確率も1千万回も回せば0.1389になる・・・こともあります。
18.2 解いてみての感想など
MathematicaのPermutationsは順列を実際にリストで並べてくれるので階乗を使った計算よりもイメージがし易いですね♪ 学生時代にこれで練習してからnCkとかで計算したかったです。
ParallelSum便利ですが、もう少し軽くなると良いですね。それと並列計算を使った後には例えカーネル再起動したとしても ノートブックの保存は忘れずに! です。![]()
続くかも。
19 PlayRange
Mathematicaを使って波形のサウンドを聴きたい事があるとおもいます。
Clear["Global`*"];
f[t_] := (Sin[2 \[Pi] 475 t] + Sin[2 \[Pi] 568 t] +
Sin[2 \[Pi] 636 t] + Sin[2 \[Pi] 790 t]);
Play[f[t], {t, 0, 3}]
これで聴くことができますが、すこしブツブツ音、アンプがサチる(飽和する)感じな音がする気がします。
関数に指数関数を乗じて音を減衰させて聞いてみると。(Mathematicaでお試しする時は音量注意!)
Clear["Global`*"];
f[t_] := Exp[-t/(1/2)] (Sin[2 \[Pi] 475 t] + Sin[2 \[Pi] 568 t] +
Sin[2 \[Pi] 636 t] + Sin[2 \[Pi] 790 t]);
Play[f[t], {t, 0, 3}]
最初に激しくブツブツ音が入ってしまいます。なんでそうなのぉ~?
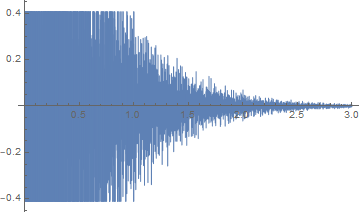
先ほどの関数をPlotしてみると、、、
Clear["Global`*"];
f[t_] := Exp[-t/(1/2)] (Sin[2 \[Pi] 475 t] + Sin[2 \[Pi] 568 t] +
Sin[2 \[Pi] 636 t] + Sin[2 \[Pi] 790 t]);
Plot[f[t],{t,0,3}]
と、このように、±0.4辺りで切られています。Plotの場合には、PlotRange->Allですが、PlayですとPlayRange->Allがあります。ので、オプションを付けて音を再生していみると・・・。
Clear["Global`*"];
f[t_] := Exp[-t/(1/2)] (Sin[2 \[Pi] 475 t] + Sin[2 \[Pi] 568 t] +
Sin[2 \[Pi] 636 t] + Sin[2 \[Pi] 790 t]);
Play[f[t],{t,0,3},PlayRange->All]
これで綺麗に音が再生されました♪
因みに電子回路シミュレータのspiceでシミュレーションした結果をサウンドにすることもできます。Importするファイルのフォルダ指定は挿入(I)のファイルパス(F)が便利です。例えば次の様な感じです。
Clear["Global`*"];
s = Import["test1.csv",
"Table"]
f = Interpolation[s, InterpolationOrder -> 3, Method -> "Spline"]
Play[f[t], {t, 0, 10}, PlayRange -> All]
spiceには下記のようなコマンドを使ってcsvを書き出します。
.tran 122us 10
.control
wrdata test1.csv "V(Out)"
.endc
Spiceの過渡解析のstepの大きさにもよるとは思いますが、0次補間やライン補間よりも綺麗な音がする・・・ような気がします。
N.お約束の純虚数
虚数は数学ではI(アイ)なので、Mathematicaもそうです。でも、電気だとJ(ジェー)で、
In[36]:= Solve[x^2 == -1, x]
Out[36]= {{x -> - J}, {x -> J}}
とか出来ると良いなぁ。