備忘録 LeetCode-142. Linked List Cycle II

はじめに

この記事はアルゴリズム振り返り用メモ，
言語化練習用に作成した記事です．

URL

Linked List Cycle II

対象者

特になし

code

main.cpp

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        //1つも要素がない場合
        if(head == nullptr || head->next == nullptr)return nullptr;
        
        //fast = 2つ先
        //slow = 1つ先
        ListNode* fast = head;
        ListNode* slow = head;
        
        //fastがnullになるまで続ける
        while(fast != nullptr && fast->next != nullptr){
            //要素更新
            fast = fast->next->next;
            slow = slow->next;
            
            //一致check
            if(fast == slow)break;
        }
        //要素がない場合 && 次の要素がない場合
        if(fast == nullptr || fast->next == nullptr)return nullptr;
        
        //初期位置に設定し直す
        slow = head;
        //slow と fast　が一致するまで続ける
        while(slow != fast){
            //両方1進める
            fast = fast->next;
            slow = slow->next;
        }
        //nodeを返す
        return fast;
    }
};

結果

Runtime: 7 ms, faster than 92.06% of C++ online submissions for Linked List Cycle II.
Memory Usage: 7.7 MB, less than 35.33% of C++ online submissions for Linked List Cycle II.

詳細

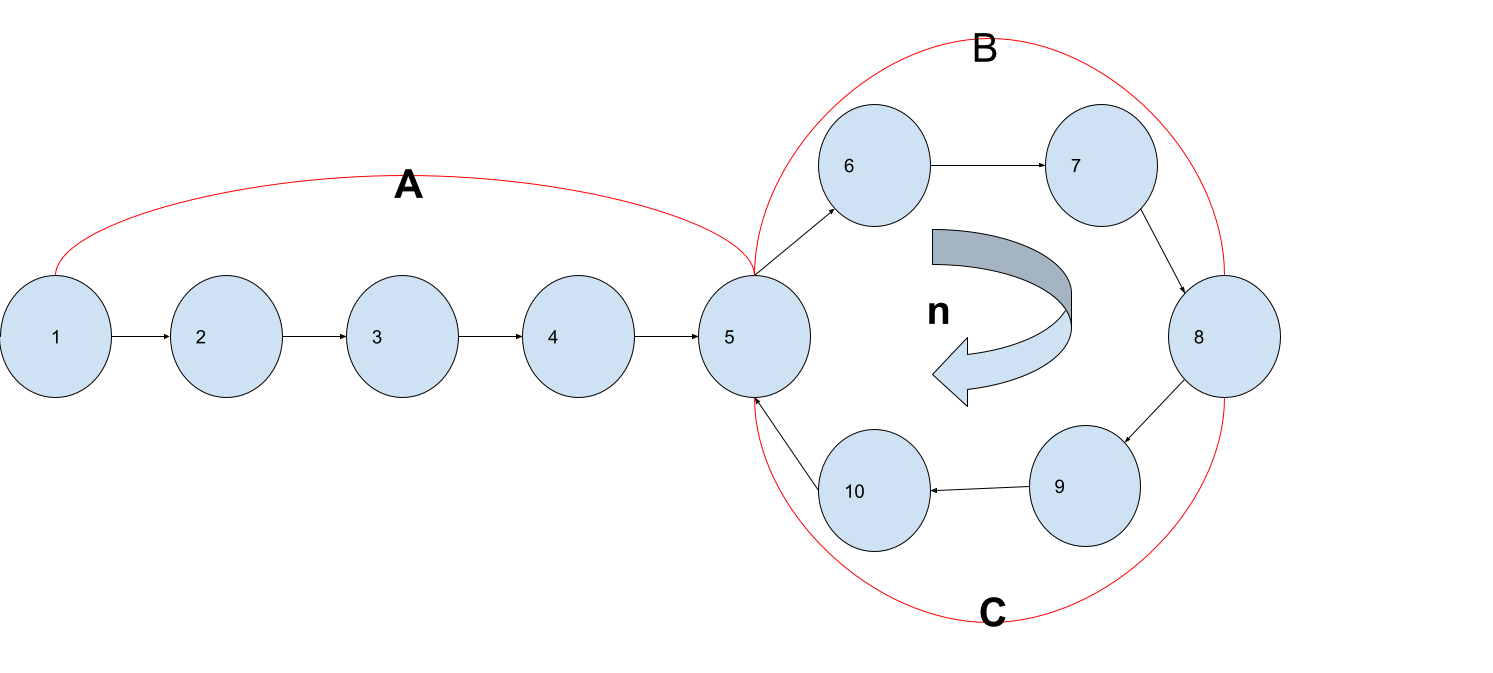
ループが始まるまでをA
ループが始まり&折り返し地点までをB
折り返し地点からループ開始地点までをC
何週したかをn

//fastはslowの2倍移動しているのでこのような式になる
fast = A+(B+C)n+B
slow = A+B
A+(B+C)n+B = A+B
2(A+B)=A+(B+C)n+B
2A+2B = A+Bn+Cn+B
A = B(n-1) + Cn
になる

nが1の場合
A = C
ループの開始位置(5)になる

nが2の場合
A = B+2C
ループの開始位置(5)になる

nが3の場合
A = 2B+3C
ループの開始位置(5)になる

nが4の場合
A = 3B+4C
ループの開始位置(5)になる

以降も同じようになる

参照

動画

おわりに

今回も前回に引き続き英語の理解に苦しめられ約40分かかってしまいました。。。
まだまだ動画等で解説を見ないと完全に理解ができないのでより頑張っていきたいです！