EWC(Elastic Weight Consolidation)を使ってCNNでMNISTの学習を確認してみた。(Chainer利用)

はじめに

ニューラルネットワークが持つ欠陥「破滅的忘却」を回避するアルゴリズムをDeepMindが開発したらしいので、元論文を読んだ。の記事を読んだので、ChainerでCNNを作成しMNISTでEWCを使った学習を行ってみたので、メモとして残します。

元論文
Overcoming catastrophic forgetting in neural networks
https://arxiv.org/abs/1612.00796

実装は以下のTensorFlow実装をChainerに書き換えて実験しました。
https://github.com/ariseff/overcoming-catastrophic

間違い、ご指摘等ありましたらよろしくお願いします。

環境

python 2.7+
chainer 1.20+ ,2.0.0a1

実装および実験

今回実装したものはこちらにあげてあります。Github

学習の流れはMNISTデータについて通常の学習(CNNなので(1,28,28)Shapeで処理）を行い。次に画像を左右反転させて学習を行った。反転画像の学習はEWC損失無し、有りで比較した。

モデル構造は以下のようになります。

この記事を作成している時に気が付きましたが、元スクリプトがNINだったのでクラス名がNINになっています・・・

ewc_cnn_mnist.py

class NIN(chainer.Chain):

    insize = 28

    def __init__(self):
        layers = {}
        layers["conv1"] = L.Convolution2D(1,   96, 3, pad=1)
        layers["conv2"] = L.Convolution2D(96,  256,  3, pad=1)
        layers["conv3"] = L.Convolution2D(256,  384,  3, pad=1)
        layers["conv4"] = L.Convolution2D(384, 11,  3, pad=1)


        super(NIN, self).__init__(**layers)
        self.train = True

        self.var_list = []#予め各パラメーターリストを保持しておく
        self.var_list.append(self.conv1.W)
        self.var_list.append(self.conv1.b)
        self.var_list.append(self.conv2.W)
        self.var_list.append(self.conv2.b)
        self.var_list.append(self.conv3.W)
        self.var_list.append(self.conv3.b)
        self.var_list.append(self.conv4.W)
        self.var_list.append(self.conv4.b)


    def clear(self):
        self.loss = None
        self.accuracy = None

    def __call__(self, x, t):
        self.clear()
        h = F.leaky_relu(self.conv1(x))
        h = F.max_pooling_2d(h, 3, stride=2)
        h = F.leaky_relu(self.conv2(h))
        h = F.max_pooling_2d(h, 3, stride=2)
        h = F.leaky_relu(self.conv3(h))
        h = F.leaky_relu(self.conv4(h))
        h = F.reshape(F.average_pooling_2d(h, h.data.shape[2]), (x.data.shape[0], 11))
        self.loss = F.softmax_cross_entropy(h, t)
        self.accuracy = F.accuracy(h, t)
        self.h = h
        return self.loss

    def predict(self, x, t,train=False):
        self.clear()
        h = F.leaky_relu(self.conv1(x))
        h = F.max_pooling_2d(h, 3, stride=2)
        h = F.leaky_relu(self.conv2(h))
        h = F.max_pooling_2d(h, 3, stride=2)
        h = F.leaky_relu(self.conv3(h))
        h = F.leaky_relu(self.conv4(h))
        h = F.reshape(F.average_pooling_2d(h, h.data.shape[2]), (x.data.shape[0], 11))
        self.accuracy = F.accuracy(h, t)
        return h

    def Fissher(self,imageset,shape,gpu,num_samples):#フィッシャー行列計算

        if gpu >= 0:
            xp = cp
        else:
            xp = np

        num_samples = num_samples

        self.F_accum = []
        for v in range(len(self.var_list)):
            self.F_accum.append(xp.zeros(self.var_list[v].data.shape))

        for i in range(num_samples):#引数のサンプル数を用いてフィッシャー行列を算出
            c,w,h = shape
            x = np.ndarray((1, c, w, h), dtype=np.float32)
            y = np.ndarray((1,), dtype=np.int32)
            rnd = np.random.randint(len(imageset))
            path = imageset[rnd][0] 
            label = imageset[rnd][1]
            x[0] = np.array(path)
            y[0] = np.array(label)
            if gpu >= 0:
                x = cuda.to_gpu(x)
                y = cuda.to_gpu(y)

            x = chainer.Variable(x)
            y = chainer.Variable(y)

            probs = F.log_softmax(self.predict(x,y))
            class_ind = np.argmax(cuda.to_cpu(probs.data))#最大確率のクラスインデックスを取得
            loss = probs[0,class_ind]#最大確率のクラスインデックスのlog_softmax値のみ抽出
            self.cleargrads()
            loss.backward()
            for v in range(len(self.F_accum)):
                self.F_accum[v] += xp.square(self.var_list[v].grad)#各パラメーターの勾配値の2乗を追加

        # divide totals by number of samples
        for v in range(len(self.F_accum)):
            self.F_accum[v] /= num_samples#使用したサンプル数で除算
        print "Fii",self.F_accum[0]

    def star(self,gpu):
        # used for saving optimal weights after most recent task training
        self.star_vars = []

        for v in range(len(self.var_list)):
            if gpu >= 0:
                self.star_vars.append(Variable(cuda.to_gpu(self.var_list[v].data)))
            else:
                self.star_vars.append(Variable(cuda.to_cpu(self.var_list[v].data)))

    def restore(self):
        # reassign optimal weights for latest task
        if hasattr(self, "star_vars"):
            for v in range(len(self.var_list)):
                self.var_list[v].data = self.star_vars[v]

    def update_ewc_loss(self, lam, gpu, model2):
        # elastic weight consolidation
        # lam is weighting for previous task(s) constraints

        if gpu >= 0:
            xp = cp     
            self.ewc_loss = self.loss
            for v in range(len(self.var_list)):
                self.ewc_loss += (lam/2) * F.sum(Variable(cuda.to_gpu(self.F_accum[v].astype(xp.float32))) * F.square(self.var_list[v] - model2.star_vars[v]))
        else:
            xp = np
            self.ewc_loss = self.loss
            for v in range(len(self.var_list)):
                self.ewc_loss += (lam/2) * F.sum(Variable(cuda.to_cpu(self.F_accum[v].astype(xp.float32))) * F.square(self.var_list[v] - model2.star_vars[v]))

        return self.ewc_loss

EWC損失の理論的詳細は解説記事やtensorflow実装によると、フィッシャー情報行列の算出は前タスクのサンプルをいくつか取り、そのサンプルのsoftmax確率からクラスを1つ選択し、該当クラスインデックスのsoftmax出力値のlog値を逆伝搬させモデルの重み、バイアス情報の勾配を算出し、全ての入力サンプルで総和を取り、サンプル数で除算します。EWC損失の計算は元々の損失に以下の式の計算値を足し合わせます。

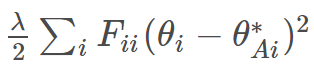
今回の実装ではsoftmax出力値のargmaxを取っているので、最大確率のクラスのみフィッシャー行列計算に関わっています。tensorflow実装ではsoftmax確率に応じてクラスを選択しています。難しいタスクになると必ずしも最大確率が当たりクラスではなくなる（上位5位以内に正解がある）といった場合にはsoftmax確率に応じたrandam選出に実装し直す必要があります。

EWC損失利用の学習部スクリプトは以下のようになっています。（1番目の学習、2番目の学習のスクリプトは省略詳細)はGithubを見てください。
train1_ewc_cnn.py → train2_ewc_cnn.py or train2_ewc_cnn_F.py(こちらがEWC利用版)の順で使用します。

train2_ewc_cnn_F.py

batchsize=320
n_epoch=10
n_epoch2=10
n_train=60000
gpu = -1#0
shape = (1,28,28)

## MNISTデータをロード
print "load MNIST dataset"
train_data, test_data = chainer.datasets.get_mnist(ndim=3)

model = ewc_cnn_mnist.NIN()
#model.to_gpu()
serializers.load_npz("out_models/train_mm_1_9.npz",model)

o_model = optimizers.Adam()
o_model.setup(model)

model2 = ewc_cnn_mnist.NIN()#学習を行わず、前回タスクの重み、バイアス情報を保持する。
#model2.to_gpu()
serializers.load_npz("out_models/train_mm_1_9.npz",model2)

model.star(gpu)#前回タスクパラメーターを保管

print "calculate Fissher matrix"
model.Fissher(train_data,shape,gpu,len(train_data))#学習を始める前に前回タスクデータを用いてフィッシャー行列を算出

model2.star(gpu)#前回タスクパラメーターを保管



def train(epoch,batchsize,train_data,test_data,mod,o_mod):

    x = np.ndarray((batchsize, 1, 28, 28), dtype=np.float32)
    y = np.ndarray((batchsize,), dtype=np.int32)
    for j in range(batchsize):
        rnd = np.random.randint(len(train_data))
        path = train_data[rnd][0] 
        label = train_data[rnd][1]
        x[j] = np.array(path)[:, :, ::-1]
        y[j] = np.array(label)

    #x = chainer.Variable(cuda.to_gpu(x))
    #y = chainer.Variable(cuda.to_gpu(y))
    x = chainer.Variable(x)
    y = chainer.Variable(y)

    loss = mod(x,y)
    loss_ewc = mod.update_ewc_loss(2000000,gpu,model2)
    acc_tr = mod.accuracy.data

    o_mod.zero_grads() #or model.creargrad()
    loss_ewc.backward()
    o_mod.update()

    #test task
    x = np.ndarray((batchsize, 1, 28, 28), dtype=np.float32)
    y = np.ndarray((batchsize,), dtype=np.int32)
    for j in range(batchsize):
        rnd = np.random.randint(len(test_data))
        path = test_data[rnd][0] 
        label = test_data[rnd][1]
        x[j] = np.array(path)[:, :, ::-1]
        y[j] = np.array(label)

    #x = chainer.Variable(cuda.to_gpu(x))
    #y = chainer.Variable(cuda.to_gpu(y))
    x = chainer.Variable(x)
    y = chainer.Variable(y)

    acc_te = mod.predict(x,y)
    acc_te = mod.accuracy.data


    #anather testtask
    x = np.ndarray((batchsize, 1, 28, 28), dtype=np.float32)
    y = np.ndarray((batchsize,), dtype=np.int32)
    for j in range(batchsize):
        rnd = np.random.randint(len(test_data))
        path = test_data[rnd][0] 
        label = test_data[rnd][1]
        x[j] = np.array(path)
        y[j] = np.array(label)

    #x = chainer.Variable(cuda.to_gpu(x))
    #y = chainer.Variable(cuda.to_gpu(y))
    x = chainer.Variable(x)
    y = chainer.Variable(y)

    acc_an_t = mod.predict(x,y)
    acc_an_t = mod.accuracy.data


    f = open("log2_F.txt","a")
    f.write('epoch' +" "+ str(epoch)+" " + str(i)+" loss " + str(loss.data)+" " +"acc_tr"+" " + str(acc_tr)+"acc_te"+" " + str(acc_te)+"acc_an_t"+" " + str(acc_an_t)
                + "\n")
    f.close
    print 'epoch',epoch,"loss",loss.data,"acc_tr",acc_tr,"acc_te",acc_te,"acc_an_t",acc_an_t

for epoch in xrange(0,n_epoch):
    for i in xrange(0, n_train, batchsize):    
        train(epoch,batchsize,train_data,test_data,model,o_model)

EWC損失を利用する際に、前回タスクパラメーターθ（model.star()によって保持されている。）は動かさないのですが、Chainerだと損失計算に関わったパラメータは全て関連されており、updateすると更新されてしまっていました。そこで仕方なくmodel2としてもう一つmodelを用意し、そちら側のmodel2.star()内のパラメーターを使うことにしました。(model2はupdateしない）何か良いやり方があればご教授いただければと思います。

その他パラメーター：

・フィッシャー情報行列算出に用いたサンプル数（前回タスクデータ全て・・・のつもりだったのですが書いてる際に見直していたら前回タスクデータ数分のランダム抽出をしていました。）
・前回タスクパラメーターの影響度λ：2000000（このぐらい大きくしないと後述結果のような忘却防止効果が得られなかった。この値で良いのか不明、実装に誤り？もう少し勉強が必要）

結果

それぞれの学習曲線を下図に示します。

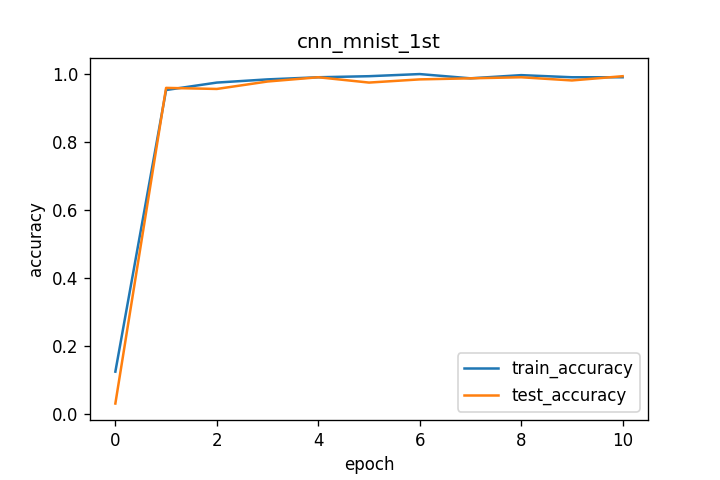
1番目のMNIST学習タスク(1st_data)ではtrain、testともにaccuracyが1.0に近いところまで問題なく学習できていると思います。

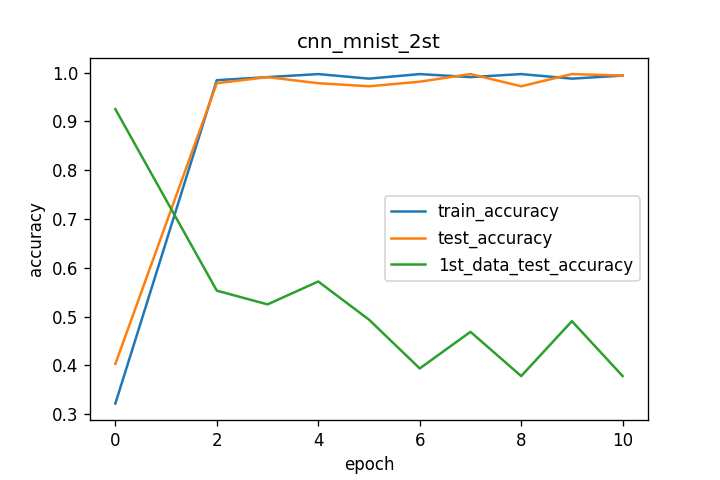
最初の学習結果を引き継いでMNISTの反転画像を学習させた際には、反転画像のtrain、test双方でaccuracyが1.0近くまで伸びていますが、それにつれて1st_dataのtest判定のaccuracyは徐々に減少しています。これにより反転画像での学習で破滅的忘却が起きていると思われます。

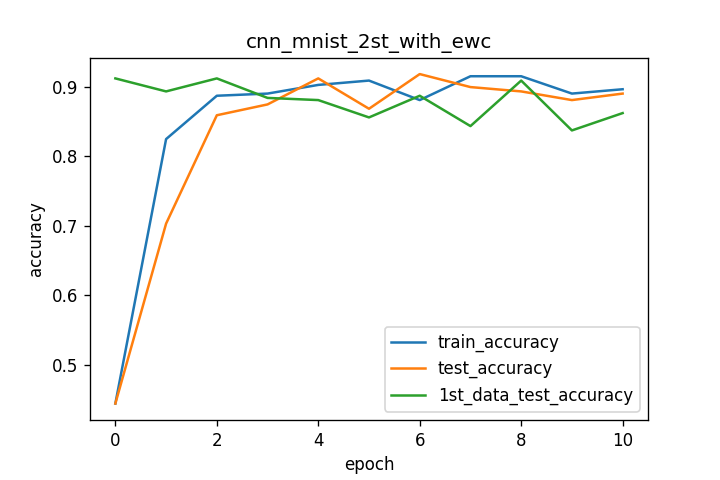
最後にewc_lossを追加した場合の反転画像の学習ですが、2番目の学習結果と異なり、train、testのaccuracyが上昇しても、1st_dataのtestaccuracyの低下が抑えられた結果となっています。しかしaccuracyの数値は0.9付近で停滞する結果となっています。

疑問メモ

解説記事にもありましたが、フィッシャー行列Fを出すのにサンプル数がどの程度必要なのか。λの値はどのように決めるのかなどなど・・・・

参考

解説記事
https://rylanschaeffer.github.io/content/research/overcoming_catastrophic_forgetting/main.html
日本語解説
http://qiita.com/yu4u/items/8b1e4f1c04460b89cac2
TensorFlow実装
https://github.com/ariseff/overcoming-catastrophic