はじめに
今回は論理パズル問題について5問ほど紹介しようと思います。
そもそもこの記事を書くきっかけになったのはある試験で「ハノイの塔」と呼ばれるパズル問題を久々に解いたときに他の論理パズルも解いてみたいと思い、以下の問題を紹介したいと思います。
答えを見ずに解きたい場合はなるべくスクロールをしないようにしてください。
(すぐ下に解説が続いてます)
- ハノイの塔
- 3枚のカード
- 昇給
- ボールの重さ
- モンティ・ホール問題
ハノイの塔
まずはハノイの塔について解説したいと思います。
ハノイの塔とはなにか?
以下のルールを守りながら、すべての円板を一番右の棒に移動させるゲームです。
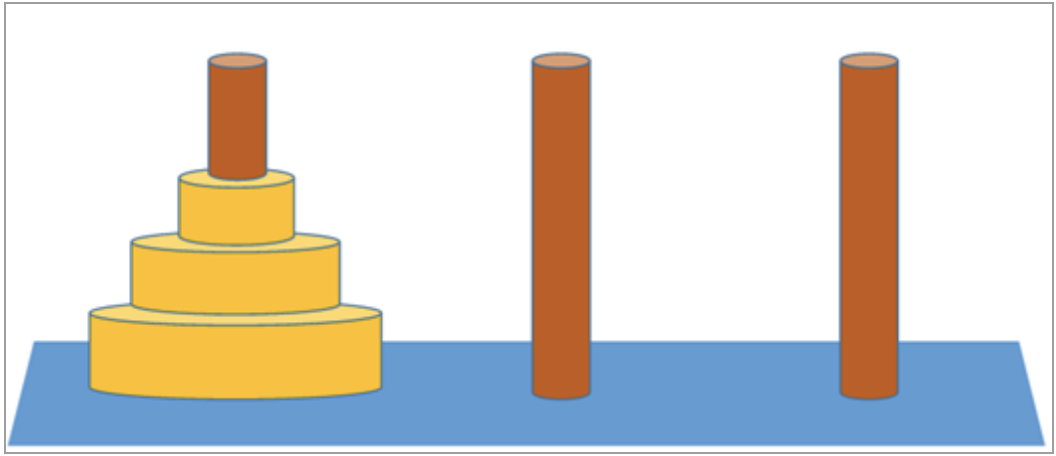
- 3本の杭と、中央に穴の開いた大きさの異なる複数の円盤から構成される。
- 最初はすべての円盤が左端の杭に小さいものが上になるように順に積み重ねられている。
- 円盤を一回に一枚ずつどれかの杭に移動させることができるが、小さな円盤の上に大きな円盤を乗せることはできない。
今回はn枚の円盤すべてを一番右の棒へ移動させる最小移動回数{n}を{n-1}を用いて表してみましょう。
少ない数で具体的に考えて視覚的イメージを掴む
例えば、円盤が1枚の場合、{1}は、1回でおしまいです。
2枚なら、{2}は「1枚目を中央へ、2枚目を右端へ、1枚目を右端へ」という3回で移動することができます。
3枚の場合、{3}はもう少し多くなります。「1枚目を右端へ、2枚目を中央へ、1枚目を中央へ、3枚目を右端へ、1枚目を左端へ、2枚目を右端へ、1枚目を右端へ」となり、7回で移動することができます。
3枚の場合、三枚目を右端へ置くために「1枚目を右端へ、2枚目を中央へ、1枚目を中央へ」の手順を踏むと思いますが、2枚の時の手順と酷似しているのがわかると思います。右端ではなく中央に2枚の塔を作っているだけです。ということはここまでの最小移動回数は{2}ですよね。

その後、3枚目を右端へ移動したあとの形を見てみましょう。

この形です。この後、3枚の塔を作るまでの最小移動回数はいくつかというともちろん{2}です。
中央から右端に2枚の塔を作る回数と同じですもんね。
すると[3]は[2]を用いて表すと
{3}={2}(中央へ2枚の塔を作る回数)+1(3枚目を右端へ移動)+{2}(中央から右端へ2枚の塔を作る回数)
なので、
{3}=2*{2}+1 と表せます。
それでは{n}はというと、
同じように**{n}=2****{n-1}+1** と表せることがわかると思います。
余談
先程の式を移項すると、
{n}+1=2**({n-1}+1)** と表せますね。
これは数学では等比数列の形です。(公比が2,初項が{1}+1=2)
(2 4 8 16 ...のような数列のことです)
なので{n}をnを使って表すと
{n}+1=2*2^(n-1) (^は累乗の意味です)
{n}=2^n-1
とこんなスッキリnを使って最小移動回数を求められるわけです。
三枚のカード
あなたの目の前に3枚のカードが置かれている。
1枚目のカードは両面が黒、
2枚目のカードは両面が白、
3枚目のカードは片面が黒、もう片面が白で塗られている。
箱の中に3枚のカードを入れてよくかきまぜ、その中の1枚を引き出した。
カードの表面は白だった。
さて、このカードの裏面が白である確率は?
解説
表にして考えてみる
直感的に行くと間違えるこの問題。
まずは3枚のカードの状態を表にしてみましょう。

ぱっと見だと今回の答えは1/2だと思いますよね。
しかし、違うんです。
この問題の肝はカードの表面が白だったという条件があることです。
なので、今回の考えるべき点は以下の3点です。
- 2枚目のカードの片面の色を見た
- 2枚目のカードのもう片面の色を見た
- 3枚目のカードのもう片面の色を見た
この3つの中で裏が白となるものは2つあるので、
答えは2/3となります。
昇給
お給料がアップすることになった。
「プランA」を選ぶと、1年に1回、10万円ずつ昇給していく。
「プランB」を選ぶと、半年に1回、3万円ずつ昇給していく。
「プランA」の給料の支払いは1年に1回、1年分。
「プランB」の給料の支払いは半年に1回、半年分。
さて、どちらのプランを選ぶべきだろうか?
解説
数学で考える
はじめ1年間の給料を500万円として、3年後のプランAとプランBをそれぞれ考えてみます。
プランA
1年目 500万円
2年目 510万円
3年目 520万円
プランB
1年目 250+253=503万円
2年目 256+259=512万円
3年目 262+265=527万円
こうしてみると分かる通り、プランBのほうが給料の増え方が大きいとわかります。
式にするとよくわかります。
プランA
{ (1年前の前半の給与 + 1年前の後半の給与) + 10 }万円
プランB
{ (1年前の前半の給与 + 6) + (1年前の後半の給与 + 6) }万円
直感で答えると間違えやすいですよね。
ボールの重さ
ボールの重さは、1kgに「ボールの重さの半分」を足したものである。
ボールの重さは何kgだろうか?
解説
式を用いて考える
一見全く数字がないので意味がわからないと思いますが、以下のように式で書けます。
(ボールの重さ)=1+(ボールの重さ)÷2
両辺に2を掛けます
2*(ボールの重さ)=2+(ボールの重さ)
右辺の(ボールの重さ)を左辺に移項すると
(ボールの重さ)=2
よって2kgが正解です。
モンティ・ホール問題
プレーヤーの前に閉じた3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。プレーヤーが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。
ここでプレーヤーは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。ここでプレーヤーはドアを変更すべきだろうか?
解説
まず、A・B・Cの3つのドアから、プレイヤーはAのドアを選択し、その後司会者がBのドアをハズレとして開けたとします。
3つの扉からプレイヤーがAの扉を選んだ時、Aの扉が正解の確立は1/3です。
逆に言うと、B・Cである確率は2/3となります。
(B:1/3、C:1/3、合わせて2/3)
そこで、答えを知っている司会者がハズレのBの扉を開けます。
司会者が答えを知っててBの扉を開けたため、残りのCの扉が正解の確率は2/3となる。
表で考えてみる
上記の解説ではいまいちピンと来ないと思うので、表に書いて整理してみます。
回答者はAの扉固定で回答するとすると、以下の場合に分けられます。

この表より、
扉を変えて正解する確率は 1/3+1/3=2/3
扉を変えずに正解する確率は 1/6+1/6=1/3
となり、扉を変えたほうが正解する確率は高いと言えます。
終わりに
有名な問題とあまり知られていない問題を取り上げてみましたが、いかがだったでしょうか。
最後のモンティ・ホール問題に関しては最初全く納得できず、ちんぷんかんぷんでしたが、
表を書くことでスッキリと解決したのをよく覚えています。
こういう問題を触ることで、直感に頼らずちゃんと書いて整理することが大事だと気付かされますよね。
世の中にはこのような問題はたくさんあるので、面白かったと感じてくれれば、どんどん挑んでいって頂ければと思います。