テーブル1個がリレーションなんですよ
巷のサイトでは複数のテーブルを連携させて運用できること指して"リレーショナル"と解説しているものがいくつかあります。
しかし、これは間違いです。
テーブル1個が”リレーション”なのです。
複数のテーブルを連携させるために結合(join)や和(union)などの操作がありますが、これらのことを指しているわけではないのです。
リレーショナルの名称は、データベースの概念を数学的に定義した"関係代数(relational algebra)(もしくは関係モデル)"に由来します。
関係代数などについてはWikipediaにも記載されているので、ご覧になった方もいると思いますが、あの説明にいまいちピンとこない方も多いのではないでしょうか。
ここでは、リレーショナルデータベースの"リレーショナル"の意味が分かる程度に"リレーション(関係)"について説明してみたいと思います。
基本は2項関係(binary relation)です
関係代数は、2項関係の項の数を任意の個数にまで拡張(一般化)した概念に関する理論です。なので、これを理解するにはまず基本となる2項関係について理解する必要があります。
というか、これを理解すれば話は終了です。
Wikipediaや書籍によると、2項関係とは
2つの集合(定義域)があり、その2つの集合の直積集合の部分集合
として定義されます。
全くピンとこないと思います。
この定義を、直感的な理解になるべく近づけるような言い換えをすると、次のようになります。
2つの集合があり、その直積集合の各要素(順序対)に対して、真理値が必ず決まる
これもわかりにくいかもしれませんが、
関係演算子(C言語では "==" とかですね。)のことです。
なんでこれが部分集合になるのかということですが、
上の本来の定義とその言い換えた定義を踏まえてもらいながら、例を使って解説していきます。
ここから2項関係の例をあげていきますが、
分かりやすくするために2つの集合は、共に実数の集合ということにします。
直積集合は、単純に xy平面 と見なせることにご留意ください。
(中学校の数学程度の素朴な理解で・・・横軸をx軸、縦軸をy軸と言いましたね)
例1 ”=” という関係
”=”(イコール、等しい)というのは2項関係です。
一番単純な例です。
かつ、2項関係の中でも重要なものでもあるので、特別に”同値関係”という名称も与えられています。
この同値関係”=”について考察してみますと、
2つの実数$x$と$y$が与えらた時(直積集合の要素 $(x,y)$ が与えられた時)、必ず、
「$x$ と $y$ は等しい」
か、
「 $x$ と $y$ は等しくない」
のいずれかが成り立ちます。(真理値が決まる。)
上の言い換えられた定義を満たしているのが分かります。
この同値関係を xy平面(直積集合)の部分集合として表すとどうなるかというと、これは $y=x$ の直線となります。(次図)
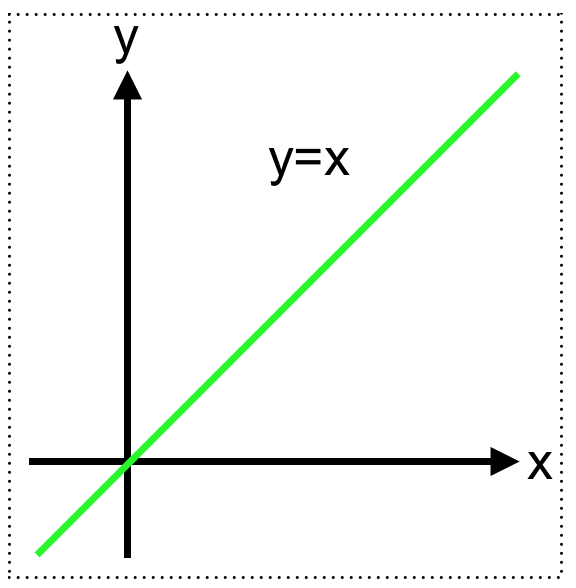
「実数 $x$と$y$ が2項関係 ”=” で真となるということは、直積集合(xy平面上)の要素(点)としてみた時、部分集合(緑色の直線)上にある。」
「実数 $x$と$y$ が2項関係 ”=” で偽となるということは、直積集合(xy平面上)の要素(点)としてみた時、部分集合(緑色の直線)上にはない。」
というふうに捉えられます。
同値関係という2項関係は、直積集合の部分集合(緑直線)によって完全に規定されることが分かります。
なんだか当たり前のことをトートロジー的に述べているだけではと感じられるかもしれませんが、さらに例を見ていってみましょう。
例2 ”>”という関係
”>”(左辺大なり)というのも2項関係です。
2つの実数 $x$ と $y$ が与えらた時(直積集合の要素 $(x,y)$ が与えられた時)、必ず真理値が決まりますね。
これを xy平面(直積集合)で表すと
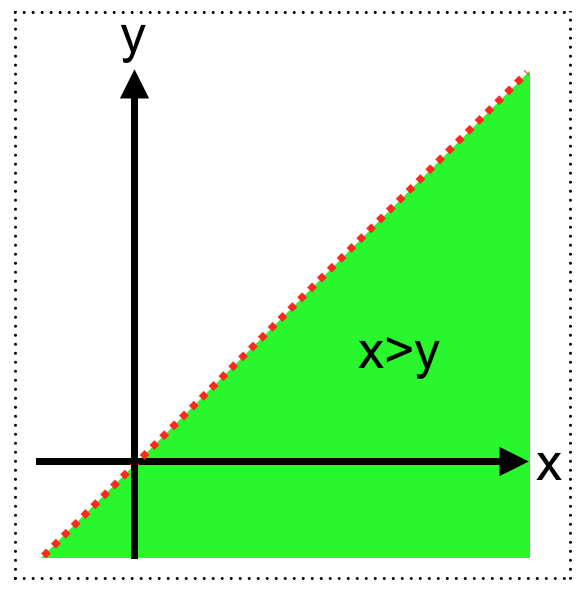
となります。
実数 $x$ と $y$(順序も大事です)に対する2項関係”>”の真理値は、座標 $(x,y)$ が緑色の領域(部分集合)に入るか入らないかということに他なりません。
上の二つの例をみると、2項関係は対応する部分集合そのものと考えることができます。
そこから「2項関係とは直積集合の部分集合とする」とすることで、具体例によらない一般化(抽象化)された定義づけがなされているということです。
”=” や ”>” はプログラミングのほか日常的もによく使われる2項関係ですが、部分集合を用いた定義によると、日常的には考えたことのないような2項関係もつくることができます。
例3 ”原点を中心とした円とその内部”という関係
原点を中心とした半径1の円とその内部の領域を合わせた領域を考えます。
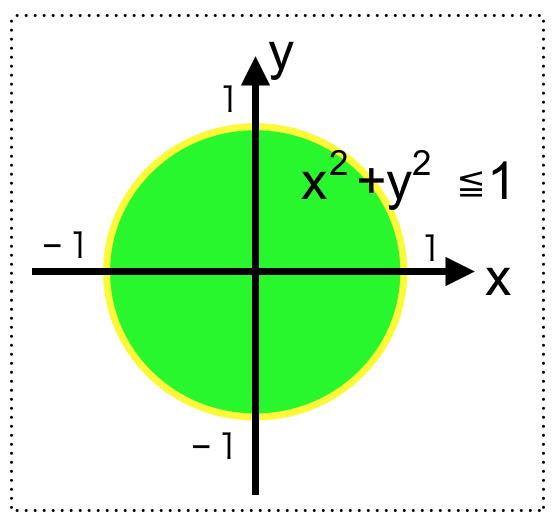
これも直積集合(xy平面上)の部分集合なので、2項関係です。
一般に”$R$"がある2項関係を表し、順序対 $(x,y)$ がこの2項関係を満たす時
xRy
と書きます。$R$のところに”=”とか”>”が入るイメージですね。
上の円の例だと、
xRy \Leftrightarrow x^2+y^2\leq1
となります
以上の例ではすべて部分集合が数式で表すことができかつ無限集合ですが、直積集合の部分集合は数式で表すことができないものもあるし、有限集合となっているものあります。
次に有限集合の例を考えてみましょう。
例4 有限集合としての関係
xy平面上の6つの点$(0,0)$,$(1,0)$,$(2,0)$,$(2,1)$,$(2,2)$,$(3,1)$からなる部分集合を考えてみます。
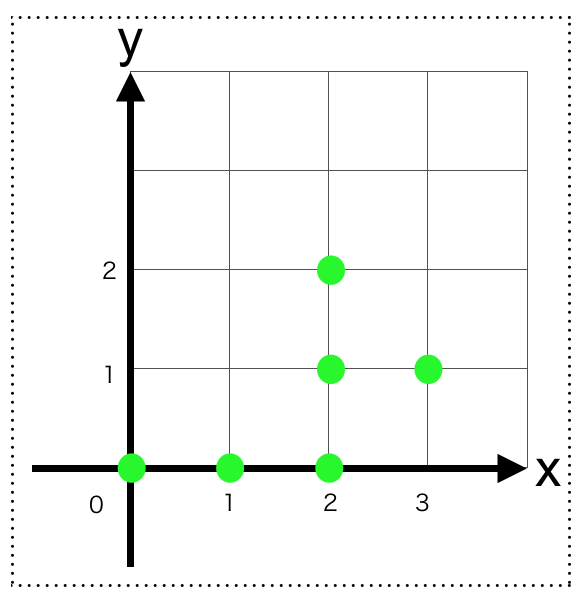
要素が有限個しかないですが、直積集合の部分集合なのでれっきとした2項関係です。
これらの部分集合の要素をまとめて次のように書くと・・・
| $x$ | $y$ |
|---|---|
| $0$ | $0$ |
| $1$ | $0$ |
| $2$ | $0$ |
| $2$ | $1$ |
| $2$ | $2$ |
| $3$ | $1$ |
となります。
これは、RDBMSのテーブルですね。
このテーブルは2項関係を表現したものであるのです。
よろしいでしょうか。
ここまでくれば、あとは2項関係をn項関係に拡張し、直積空間のベースとなる定義域を任意の集合に広げて考えればいいだけです。
またRDBMSで扱われるリレーションは有限集合のみということになります。
テーブルを、関係(リレーション、直積集合の部分集合)として見ることができるようになりましたでしょうか。
テーブルが(直積集合の部分)集合を表現したものであることが理解できれば、レコードに順番がないことや、NULLを要素として含まないないということは当然の要請として理解できます。
ちなみに、結合(JOIN)や和(UNION)などのテーブルへの操作は、「演算」と呼ばれます。
「関係(集合)」の集合上に、「演算」という代数的な構造を見出したということが、すごいところなんだと思います。
(だから関係代数というのです。)