初めに
プログラミングなどの実装技術はなくとも、脳科学の知見に基づいて生物模倣的、神経回路的にニューロコンピュータの原理的な設計をしてみたい!
と、なんともわがままな思想の元、個人的にAIに関する研究をしております。具体的な実証コードや検証データはありませんが、とりあえずAIに関する概念コンセプト的な検討提案として見てもらえれば(こんなのQiitaに投稿していいものかどうか・・・)。
ニューロアトラクタ回路とは?
現在の脳科学の知見では、その情報処理上の観点で「大脳新皮質」と「海馬体」と「大脳基底核」の3つの部位の連携が特に重要な機能を果たしていると言われているようです。しかし、いずれの部位も解剖学的、神経回路的に解析すると恐ろしいまでに複雑な回路構成にあるようで、「こんなのリバースエンジニアリングなんてできるか!」と誰もが投げ出したくなる状況のようです。
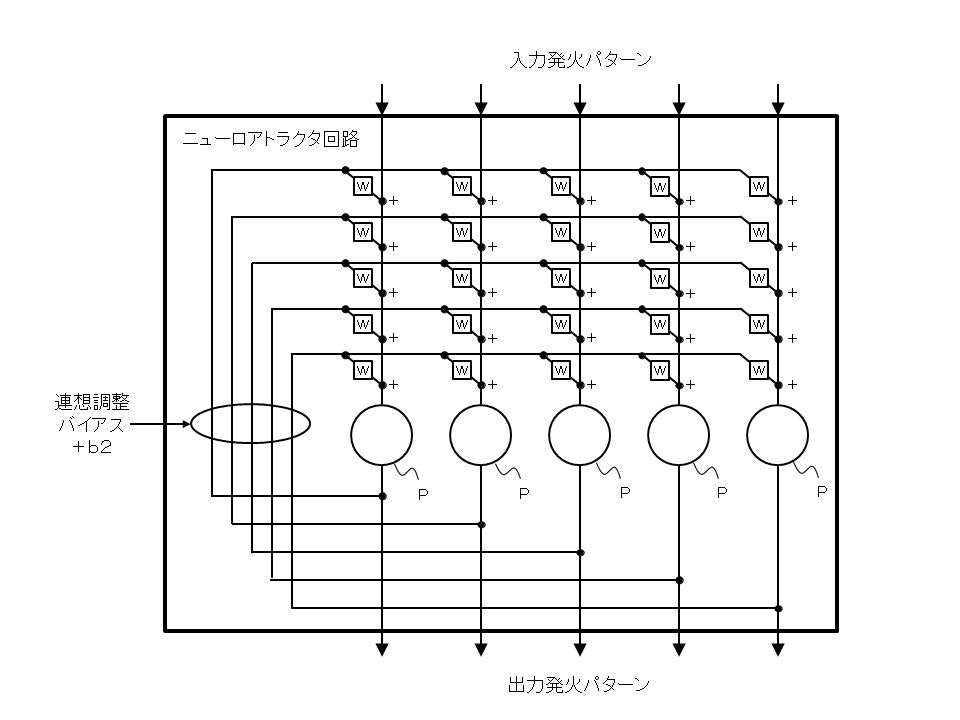
そんな中、海馬体の内部に組み込まれている「CA3野」という部位については、以前よりその回路構成と処理機能が比較的解明されており、その役割などについて注目されているようです。このCA3野の実体についてシンプルな模式図で表すと、下の図1に示すようなニューロ回路モデルの構成となるようです。
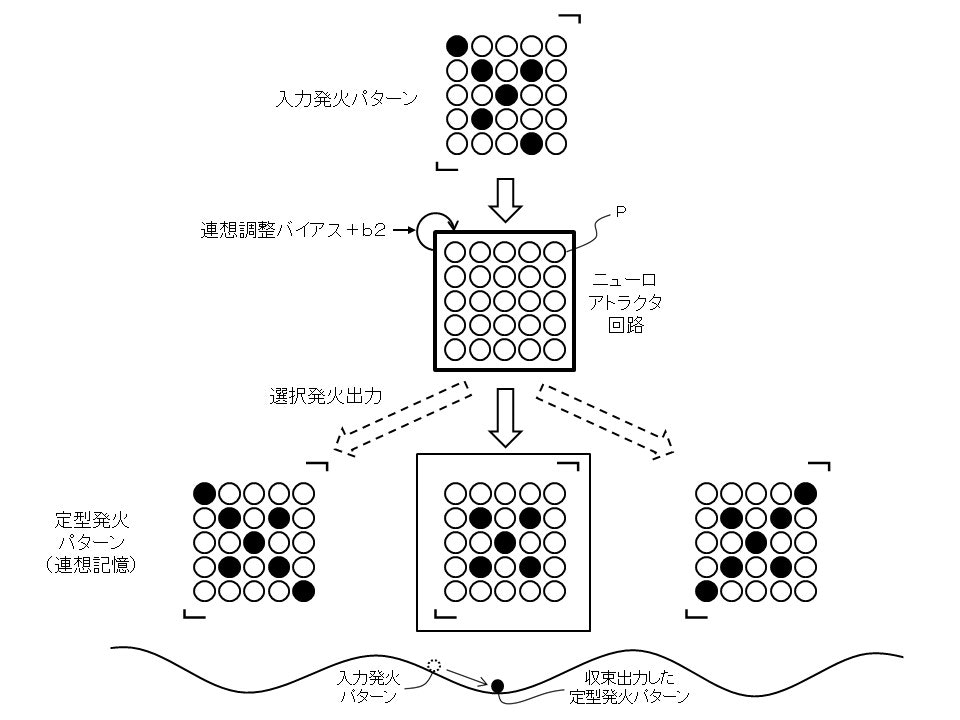
この回路モデルの構成は、概略的に言うと「多数のパーセプトロンPが単一層で全回帰結合したもの」となり、図1中では図示の理解が容易なように5つのパーセプトロンで構成された例で示しています。全回帰結合なので5^2=25個の重み計数wを備えていることになります。このようなニューロ回路は全ての重み計数wをそれぞれ適切に調整(学習)することで、内部的に特定の定型発火パターンを複数記憶することができ、入力された発火パターンに対してその発火分布に近いいずれかの定型発火パターンに収束して出力するよう機能するそうです(例えば25個のパーセプトロンを備えた場合の図2参照)。
このように離散化された特定の収束点に安定化する現象はいわゆるカオス力学系における「アトラクタ」に相当するとのこと。これに基づいて、本記事においては当該回路モデルを「ニューロアトラクタ回路」と呼称することにします。記憶できる定型発火パターンの数は回路が備えるパーセプトロン数の約15%に相当する数であり、参照した論文や一般的な学説によれば人間の海馬体におけるCA3野で約数百万個のニューロンを備え、約数万個の定型発火パターンを記憶しているとの話しです。
ニューロアトラクタ回路の利用についての検討
そこで、このような特徴的な機能を有するニューロアトラクタ回路を何か現在のAI技術に組み込んで有効に利用できないものか?といろいろ検討してみたところ、多クラス分類タスクモデルの出力層に使えるのではないかと。
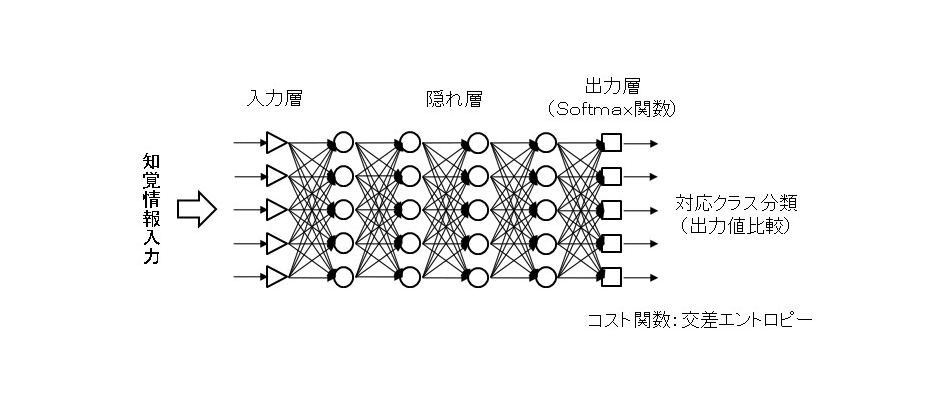
例えばこれまでの一般的な多クラス分類タスクのフィードフォワード型ニューラルネットワークモデルでは、下の図3に示すように交差エントロピーのコスト関数に基づくSoftmax関数ノードを出力層として確率密度分布ベクトルの表現でクラス分類を出力していました。
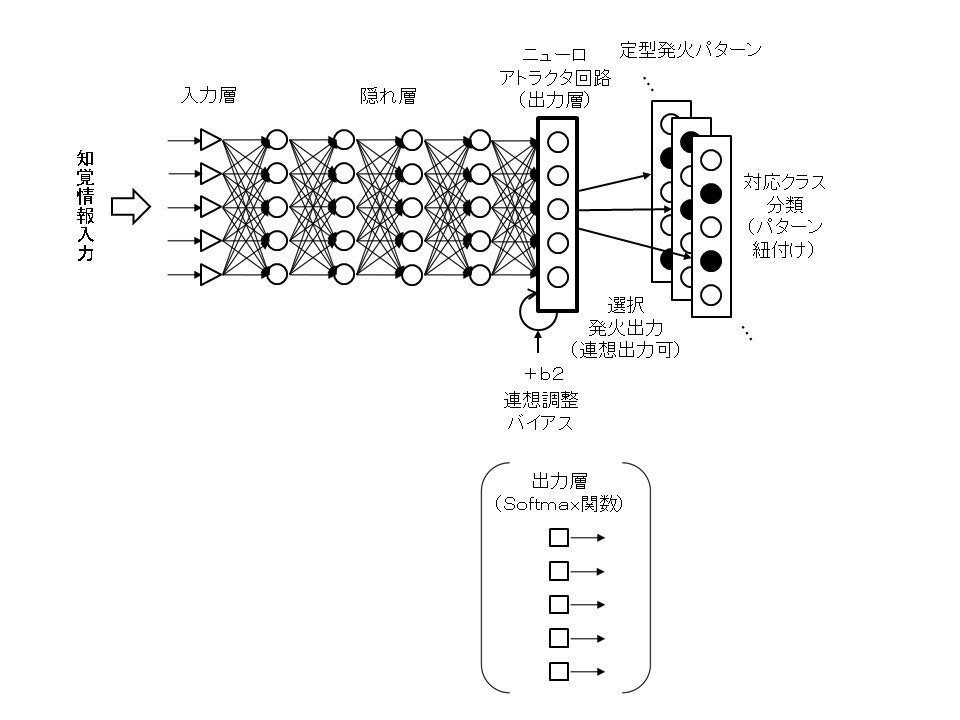
これに対して、下の図4のように出力層だけをニューロアトラクタ回路に置き換えた構成としても、その離散的な定型発火パターンの選択的出力により同様の多クラス分類が可能ではないかと考えます。この場合に現在想定し得る学習手法としては、一度上記のように生成した多クラス分類の学習済みモデルの出力層だけをニューロアトラクタ回路に置き換え、入力層から隠れ層までは既存のものを利用したまま当該ニューロアトラクタ回路の出力層だけに対して各分類クラスに対応する定型発火パターンを記憶させるよう再度教師有り学習(重み計数wを調整、但しバックプロパゲーションではない新たな学習)させることが考えられます。そして運用時には、ニューロアトラクタ回路が出力する複数の定型発火パターンの紐付けで分類させることになり、また回路全体の回帰経路に適宜の連想調整バイアス+bを連続的に増減付加することで意味合い的に近い複数の定型発火パターンを連想するよう切り替えできる可能性も考えています。
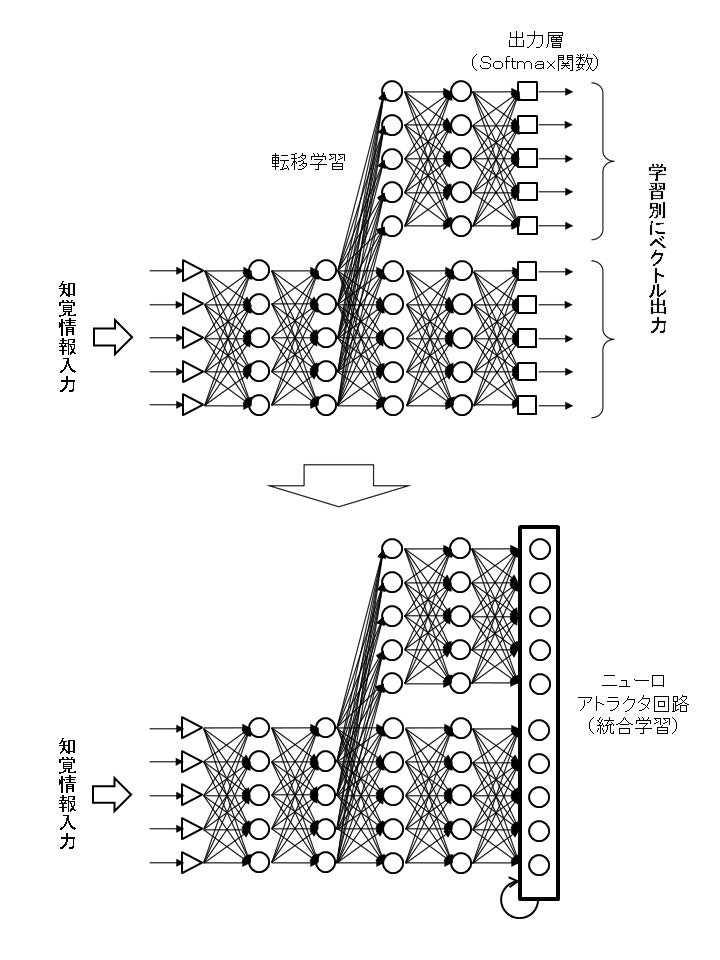
とは言え、現在のところ上記のようなニューロアトラクタ回路に対する学習での具体的な数理演算処理についてはまだ検討中であり、とりあえずここではその適用可能性についての提案だけとなります。中途半端ですみません。そして上記の手法では入力層と隠れ層における学習と、ニューロアトラクタ回路の出力層における学習とを別途に行う二度手間にはなりますが、それを補うだけの汎用性能上の利点もあるように思われます。すなわち、下の図5に示すように、これまで既存の多クラス分類モデルで転移学習を行った場合には、その学習ごとに出力層のベクトル出力を個別に扱う必要がありましたが、これに対して転移学習を繰り返した後にまとめてニューロアトラクタ回路の出力層に置き換えて統合学習させれば単一的な出力として拡張できる可能性があると思われます。
ただ、上述したように人間の海馬体が備えると同等の規模のニューロアトラクタ回路を想定した場合には重み計数wの数が途方もなく膨大となり、それらを介した回帰積和演算処理を同時平行的に協調制御させる必要があるため、これをソフトウェア的に実装するとしたら恐らくスーパーコンピュータまで使わないと実現が難しいように思われます。もしくは、いわゆるニューロモーフィックデバイス(ハードウェア電子回路で実装したニューラルネットワーク)を設計する必要があるかもしれません。
最後に
そして最後に、ここまで読まれた方に是非ともお願いしたいことがありまして、もし海馬体における「歯状回」と「CA1野」の各機能部位について、上記ニューロアトラクタ回路のように明確なニューロ回路的構成をご存じの方がいましたら何卒コメントなどでご教示頂けませんでしょうか?CA3野については上述のようなニューロ回路モデルとしての構成と機能を明確に知見できているのですが、歯状回とCA1野については具体的な回路モデルが不明であり、私自身がこれまで書籍やネットでいくら調べても解剖学的な構造説明や臨床学的見地で推定される機能などのような説明しかなく、情報処理的な機能が明確な回路構成としての知見をどうしても得ることができません。私のアカウントへの直接的なご連絡でも構いません。どうぞよろしくお願いします。