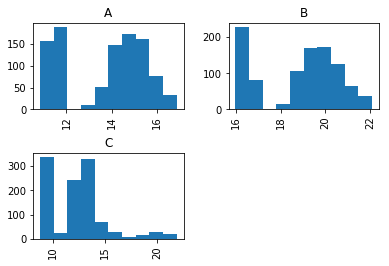現実の世の中に存在するデータには、常に外れ値が含まれる
実際にデータ分析をする際に厄介なのは、その外れ値がモデルで予測しようとするタイミングまでに知りうる情報で説明できるタイプのものなのか、説明できないタイプのものなのかで扱いが大きく変わってくるところ
今回は、irisデータ(アヤメの花弁や萼片の長さや幅が記録されたサンプルデータ)を多少加工して異常データを生成し、異常値が予測の問題に与える影響を見ていきたい
irisデータを加工
まずは、通常のirisデータを異常値が含まれるようなデータに加工していく
from sklearn import datasets
import pandas as pd
iris = datasets.load_iris()
# 花弁の長さや幅の情報が入っているデータ
df_feature_iris = pd.DataFrame(iris['data'],columns=['sepal_length','sepal_width','petal_length','petal_width'])
# 花の種類に関する情報が入っているデータ
df_species_iris = pd.DataFrame(iris['target'],columns=['species'])
# 今回は、種を特定する問題にするわけではないので、マージ
df_iris = pd.concat([df_feature_iris,df_species_iris],axis=1)
scikit-learnに格納されているirisデータセットのままだと件数が少ないため、リサンプリングして疑似的にデータを増幅させる
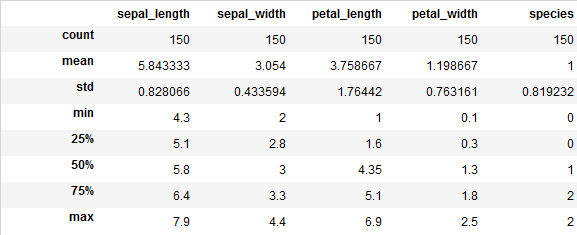
ちなみに元データの基礎統計量は↓
単純にリサンプリングしても面白くないので、多少値にバラツキを持たせておきたい
今回は、採取される地点によって花弁の長さ(petal_length)や萼片の長さ(sepal_length)が異なる状況を生成してみる
# エリアごとに長さが異なるようにばらつかせる
dict_area = {'A':10,'B':15,'C':8}
df_concat = pd.DataFrame()
list_cols = ['sepal_length','sepal_width','petal_length','petal_width']
n_sample = 1000
sigma = 0.1
for k,v in dict_area.items():
df_resample = resample(df_iris,n_samples=n_sample)
for col in list_cols:
df_resample[col] = df_resample.loc[:,col].apply(lambda x : x + random.gauss(v,sigma))
df_resample['area'] = k
df_concat = pd.concat([df_concat,df_resample])
# エリアによってどう長さが変わったかをチェック
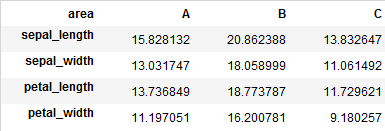
df_concat.groupby('area')[list_cols].mean().T
エリアBが他のエリアよりも発育がいい感じになるようにデータ生成が完了
異常値を生成
エリア別に花弁の長さが異なるデータを生成できたので、このデータの中に通常では観測されないような異常なデータを含ませる
今回は、エリアCの特定のアヤメだけ花弁の長さ(petal_length)がエリアCにしては異常に大きい異常なサンプルを10件だけ意図的に含ませてみる
dict_area = {'C':8}
list_cols = ['sepal_length','sepal_width','petal_length','petal_width']
# 異常な値にする列を指定
target_col = 'petal_length'
# 異常の発生数
n_sample = 100
sigma = 0.1
for k,v in dict_area.items():
df_resample = resample(df_iris,n_samples=n_sample)
for col in list_cols:
if col != target_col:
df_resample[col] = df_resample.loc[:,col].apply(lambda x : x + random.gauss(v,sigma))
else:
anomaly_value = 15
df_resample[col] = df_resample.loc[:,col].apply(lambda x : x + anomaly_value)
df_resample['area'] = k
df_anomaly = pd.concat([df_anomaly,df_resample])
異常値の分布を確認
エリアCの花弁の長さだけを異常に長くしたので、分布をみればわかりそうなものだけど
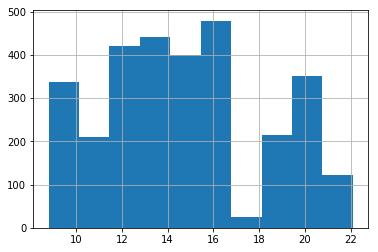
異常値が含まれないpetal_lengthの分布
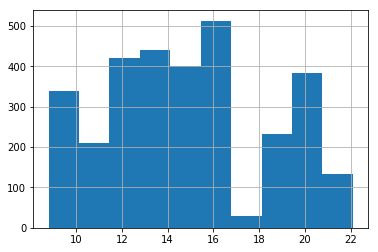
異常値が含まれるpetal_lengthの分布
うーーん、パッと見ても何がちがうかわからない。。
でも、これはそうなってくれてOK。
エリアCの異常値は、エリアBの通常のpetal_lengthの長さと近いために1変量だけで見ていてはそもそも外れ値としてはわからない
エリア毎に分布を見てみると
異常値が含まれないエリア毎のpetal_lengthの分布
異常値が含まれるエリア毎のpetal_lengthの分布
エリア毎に見るとエリアCの通常のpetal_lengthの長さとは大きく外れた部分がちゃんと存在することがわかる
しかし、数が少数なのとエリアBの長さのボリュームゾーンと一致しているため全体で見ているとこれが異常だということには気づくのは困難
このように、複数の要素を掛け合わせて観察しないと異常なデータなのか正常なデータなのかを判定しにくい場面というのは分析をしているとよく出くわす
こんな時に、ひたすら異常なデータを見つけるためにクロス集計をしていると心が枯れ果ててしまうので、異常検知の手法を用いて異常値を見つける
異常値の有無による精度差を比較
異常値検出アルゴリズムを適用して異常値を除去したモデルを作る前に、異常値が含まれることによる精度差を比較しておく
まずは、通常の状態と同じように評価用データを作成
# 評価用データ作成
dict_area = {'A':10,'B':15,'C':8}
df_predict_tmp = pd.DataFrame()
list_cols = ['sepal_length','sepal_width','petal_length','petal_width']
n_sample = 100
sigma = 0.1
for k,v in dict_area.items():
df_resample = resample(df_iris,n_samples=n_sample)
for col in list_cols:
df_resample[col] = df_resample.loc[:,col].apply(lambda x : x + random.gauss(v,sigma))
df_resample['area'] = k
df_predict_tmp = pd.concat([df_predict_tmp,df_resample])
モデリングできるように、カテゴリ変数をダミー化
# カテゴリ変数のダミー化
df_train_norm = pd.get_dummies(data=df_concat,columns=['species','area'])
df_train_anomaly = pd.get_dummies(data=df_anomaly,columns=['species','area'])
df_predict = pd.get_dummies(data=df_predict_tmp,columns=['species','area'])
通常のデータで学習して予測を実施
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
import numpy as np
# 通常のデータで学習し、評価
rfr_norm = RandomForestRegressor(criterion='mse',n_estimators=50,random_state=0)
rfr_norm.fit(X=df_train_norm.loc[:,list_feature],y=np.ravel(df_train_norm.loc[:,list_target]))
ar_predict_norm = rfr_norm.predict(X=df_predict.loc[:,list_feature])
print(mean_squared_error(df_predict.loc[:,list_target], ar_predict_norm))
# 異常値を含むデータで学習し、評価
rfr_anomaly = RandomForestRegressor(criterion='mse',n_estimators=50,random_state=0)
rfr_anomaly.fit(X=df_train_anomaly.loc[:,list_feature],y=np.ravel(df_train_anomaly.loc[:,list_target]))
ar_predict_anomaly = rfr_anomaly.predict(X=df_predict.loc[:,list_feature])
print(mean_squared_error(df_predict.loc[:,list_target], ar_predict_anomaly))
MSEで比較した場合の結果は以下の通り
| 通常 | 異常値 |
|---|---|
| 0.065 | 0.341 |
やはり異常値が含まれたデータをなにも工夫せずにモデリングするとだいぶ精度が悪化している
異常値検出
代表的な異常検知アルゴリズムにOne-Class SVMやIsolationForestなどがあるが、今回は細かな説明は省いて早速使ってみたい
さきほどの異常値が含まれたデータのうち、5%が異常なデータだと仮定して異常値検出を実施する(本当の比率は5%ではないが、異常がどれだけ含まれているかを事前に知るのは大抵の場合困難なので、複数試してみて最終的にMSEが最小になった異常値の比率を採択する
# One-Class SVMで異常検出を実施
from sklearn.svm import OneClassSVM
# 5%異常値が含まれると設定する
ocsvm = OneClassSVM(nu=0.05)
# 予測対象も含めて異常検出モデリング
list_outline = list_feature + list_target
ocsvm.fit(X=df_train_anomaly.loc[:,list_outline])
# 異常値の除去が目的なので自身に適用
y_pred_svm = ocsvm.predict(df_train_anomaly.loc[:,list_outline])
df_train_anomaly['out_flg'] = y_pred_svm
# 異常判定されたレコード out_flg=1を除外
df_train_exclude = df_train_anomaly.loc[df_train_anomaly.out_flg==1,:]
異常値除去後のデータで再度精度検証
上記で作成した、df_train_excludeを用いて再度精度評価を実施してみる
おそらく、多少は精度がマシになっているはず
# 異常値を除去したデータで学習し、評価
rfr_exclude = RandomForestRegressor(criterion='mse',n_estimators=50,random_state=0)
rfr_exclude.fit(X=df_train_exclude.loc[:,list_feature],y=np.ravel(df_train_exclude.loc[:,list_target]))
ar_predict_exclude = rfr_exclude.predict(X=df_predict.loc[:,list_feature])
print(mean_squared_error(df_predict.loc[:,list_target], ar_predict_exclude))
| 通常 | 異常値 | 異常値除去 |
|---|---|---|
| 0.065 | 0.341 | 0.266 |
多少マシになった
しかし、異常検知アルゴリズムの精度が低いのかいまいち改善されていない
異常値の比率を適当に決めすぎたので、パラメータサーチをしてどの比率なら
いい感じになるか最後に検証する
3000件の学習データに100件の異常データを含めているので、真の異常値は100/3100=0.3%なのだけれど、それほど検出精度が高くないことも考慮して異常値とみなす比率を最大で30%程度まで広げて精度を確かめる
# 異常値比率の候補リスト
list_params = [0.005 ,0.01 ,0.03 ,0.05 ,0.1 ,0.15 ,0.2, 0.25,0.3]
for param in list_params:
ocsvm = OneClassSVM(nu=param)
list_outline = list_feature + list_target
ocsvm.fit(X=df_train_anomaly.loc[:,list_outline])
y_pred_svm = ocsvm.predict(df_train_anomaly.loc[:,list_outline])
df_train_anomaly['out_flg'] = y_pred_svm
df_train_exclude = df_train_anomaly.loc[df_train_anomaly.out_flg==1,:]
#異常とみなす比率が異なるので、何件学習に用いるのかを取得しておく
cnt_record = len(df_train_exclude)
rfr_exclude = RandomForestRegressor(criterion='mse',n_estimators=50,random_state=0)
rfr_exclude.fit(X=df_train_exclude.loc[:,list_feature],y=np.ravel(df_train_exclude.loc[:,list_target]))
ar_predict_exclude = rfr_exclude.predict(X=df_predict.loc[:,list_feature])
print(param,cnt_record,mean_squared_error(df_predict.loc[:,list_target], ar_predict_exclude))
結果としては、15%に設定した場合が最良の結果となった
| 設定異常比率 | 学習件数 | 精度(MSE) |
|---|---|---|
| 0.5% | 3085 | 0.336 |
| 1% | 3067 | 0.345 |
| 3% | 3003 | 0.287 |
| 5% | 2944 | 0.266 |
| 10% | 2788 | 0.201 |
| 15% | 2637 | 0.071 |
| 20% | 2483 | 0.077 |
| 25% | 2326 | 0.086 |
| 30% | 2171 | 0.098 |
真の異常比率が3%程度ということを考えると、100件の異常データを排除するために3100-2637=463件と4倍以上のデータを取り除く必要があったことになる
うーむ、かなり効率が悪い。。。
実際に、異常値処理してモデルを改善させるにはあまりにデータを除外しすぎなので、異常値検出ロジック自体を見直す必要がありそう
ただし、全体の15%に該当する2637件をランダムに抽出した場合にはMSEは0.515とさらに精度が悪化することから、異常検出精度はそれほどでないにしてもモデルの安定には寄与しているといえそう
まとめ
今回のデータは疑似的に異常値を生成・検出し、予測モデルに反映したため極端な結果になってしまった感はあるが、現実のデータでは異常とみなすことのできるデータの割合やその異常を説明できるだけの特徴量がいつも既知とは限らないので、今回のアプローチも悪くないと思われる
おしまい