はじめに
今日も今日とてSimulink Desktop Real-Time(SDRT)で遊んでいるわけですが、秋口の忙しさを乗り切った自分へのご褒美としてDAQボードを買ってSDRTと連携したレポートです。
- Simulink Desktop Real-Time(MATLAB blog)：Simulinkモデルの実行時間を実時間同期して(ソフト)リアルタイム実行できるアドオン。
- DAQ(Data Acquisition)ボード：名の通り、PC外部の物理量のデータを取得を行う、アナログ・デジタルI/Oを多数備えたPC用の拡張基板です。
まとめ
- 新品・安価となるとPCI接続+PCI/PCIeコンバータの構成がよさそう。
- Connected I/Oモードでの動作は問題なく、単純なデジタル出力のオンオフなら1 msぐらいまでならジッタ・欠損なし。
- Serial I/FのArduinoと比較してコストも速度も数倍といった感じ。
- 正直コスパは・・・
SDRT対応DAQ
SDRTに対応したDAQはこちらにまとめられています。I/Fごとに価格帯をまとめると下表のようになります。
| I/F | 価格帯 | 備考 |
|---|---|---|
| PCI | 数万円 | 型落ち品が多く、ほかのI/Fに比べ安価 |
| PCIe | 十万～数十万円 | 新しめの製品が多く高価 |
| Thunderbolt | ？？？(見たとき10万円ぐらいだった気がする) | Humusoft MF644のみだがメーカーページに記載なし(EOL？) |
I/Fの取り付け容易性の観点ではThunderbolt接続のHumusoft MF644が非常に魅力的で、前述のMATLABブログで取り上げられているのもこちらなのですが、メーカーページに行っても商品一覧から消えていました・・・明示的なEOL情報もなかったように思うのですが、もしかしたら終売なのかもしれません。
PCIかPCIeでいうと趣味ユースならばそこそこの性能で価格が安いPCI接続の機材がよいのですが、問題はPCI規格自体が古すぎて4年落ちの私のPCにすら搭載されていないということです。
そこで、研究室では鉄板の「PCI-PCIeコンバータを使ってPCIeスロットに接続する」というテクニックでSDRTとの連携をテストしました。
装置構成
今回、DAQはAdvantech製のPCI-1711U-CEを使用します。アナログ入力16 ch、アナログ出力2 ch、デジタル入力16 ch、デジタル出力16 chを備え、アナログI/Oは12 bits, 100 kS/s動作します。
https://www.advantech.com/ja-jp/products/1-2mlkc9/pci-1711/mod_b8ef5337-44f0-4c36-9343-ad87d01792d1
Mouserで4万円台。
https://www.mouser.jp/ProductDetail/Advantech/PCI-1711U-CE?qs=HSwFsqQPTVM9dM78QJihAA%3D%3D
PCI-PCIeコンバータはこちらのものを使用しました。3000円ぐらい。
https://www.area-powers.jp/product/pcie/4580722559063/
実物写真は以下の通りです。
テスト
以下で、実際にSDRTとDAQを連携させた結果を示します。なお、以下の検証はすべてConnected I/O Mode、つまりモデルはPC上で実行されており、DAQではI/Oのみを行っている点に注意してください。
悲しいけどおれ、HOMEライセンスなのよね。
使用したPCのスペックは以下の通りです。
CPU: Intel(R) Core(TM) i7-8700
RAM: 32 GB
OS: Windows 11 Home
ループバック
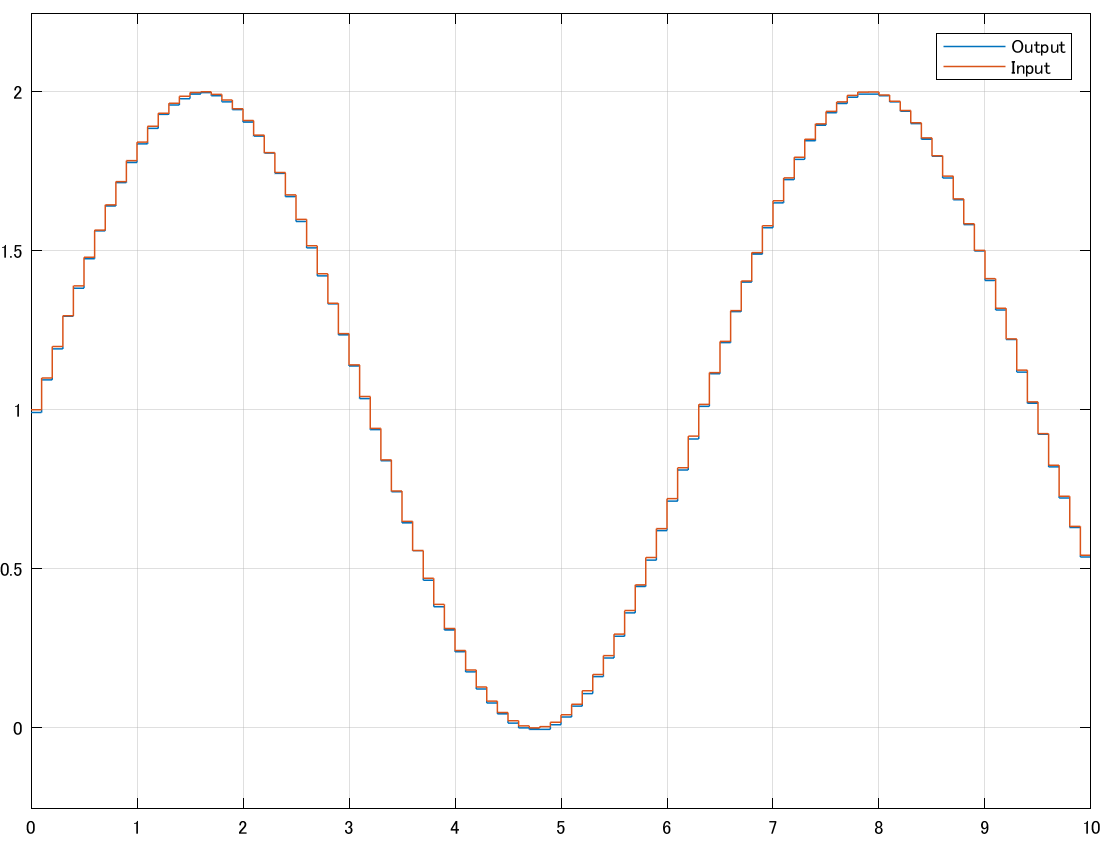
まずはこの装置構成での動作確認のため、DAQのアナログ出力とアナログ入力を接続し、1 rad/sの正弦波をループバックして観測します。アナログ入出力のサンプリング周期は0.1 sを設定しました。
Scopeの出力結果を下図に示します。ほぼ同振幅の正弦波が観測でき、最低限の入出力機能は確認できました。
リアルタイム性テスト
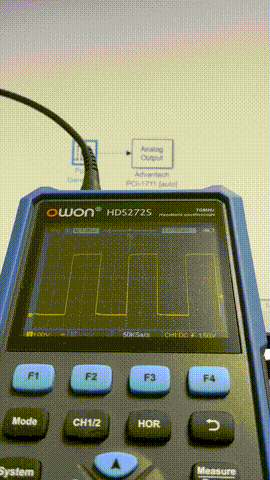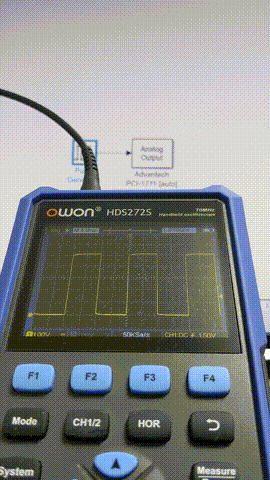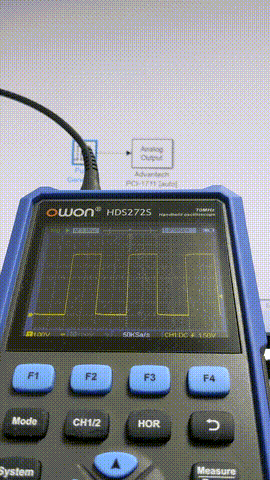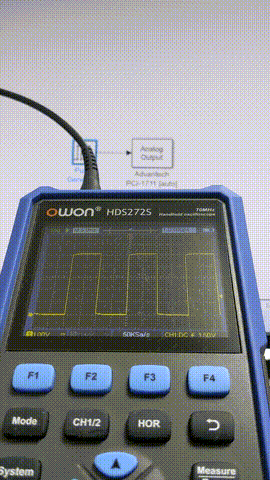
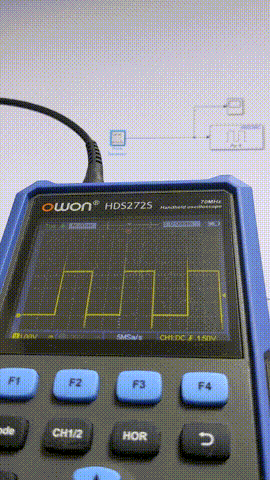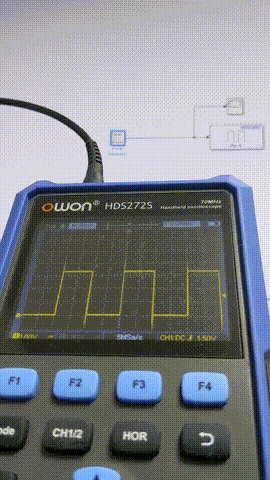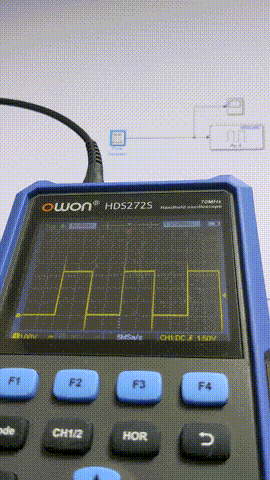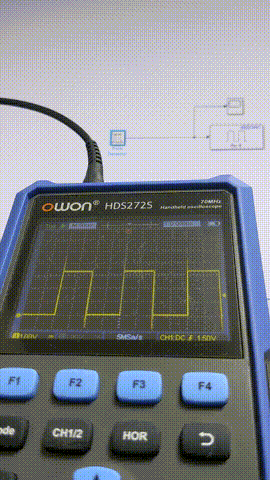
以下ではPulse Generatorにより1サンプル幅のパルスを生成しAnalog Outputから出力、出力された信号を観測することで、ジッタやフレーム飛びがないかをサンプリング周期を変えながら確認します。
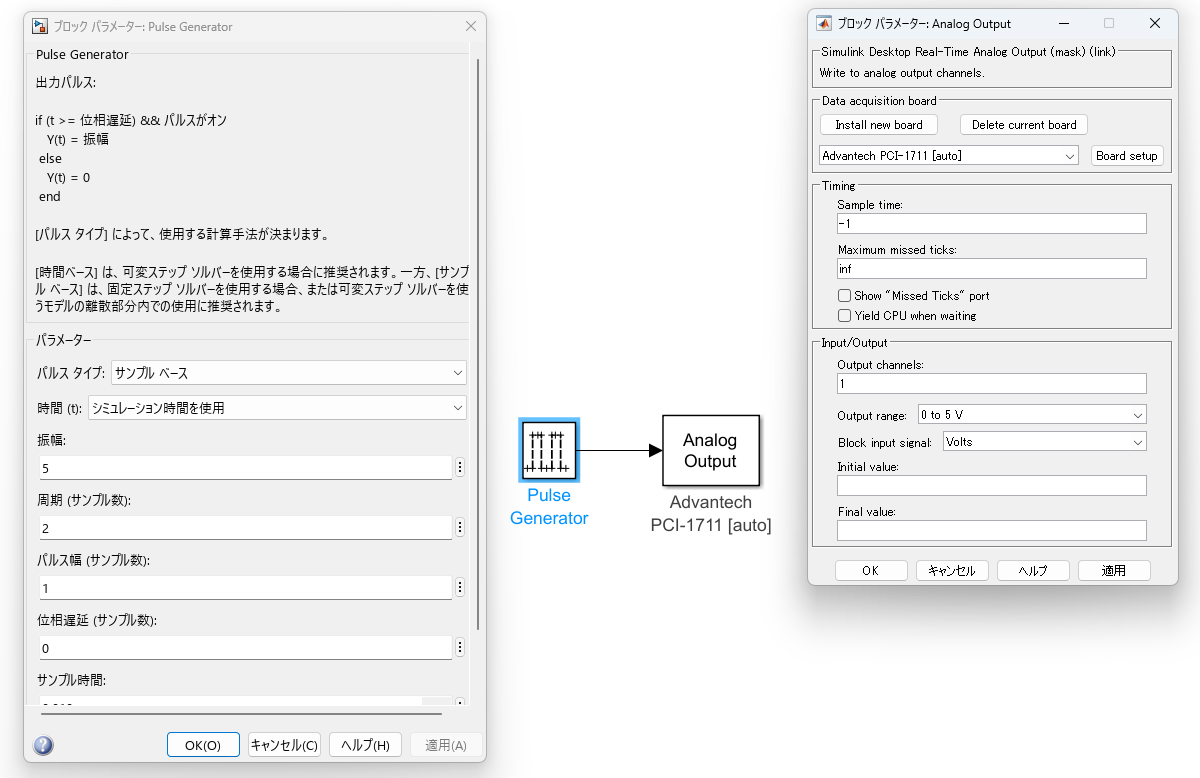
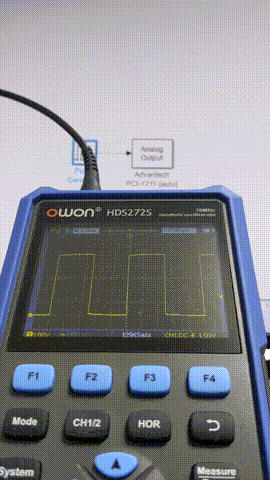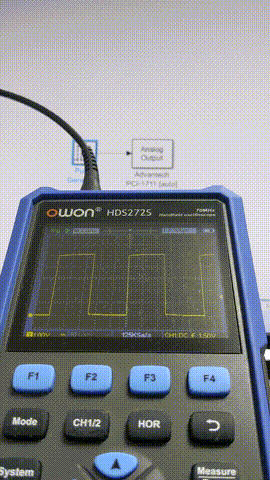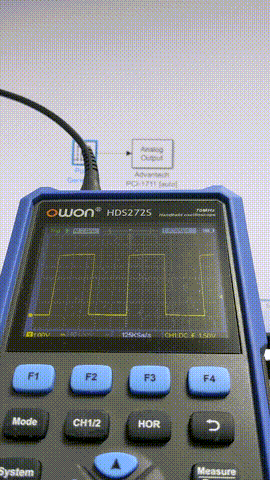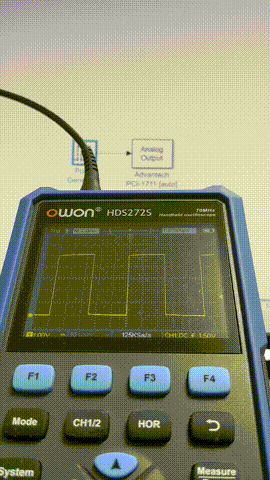
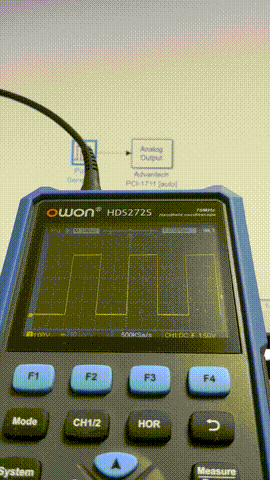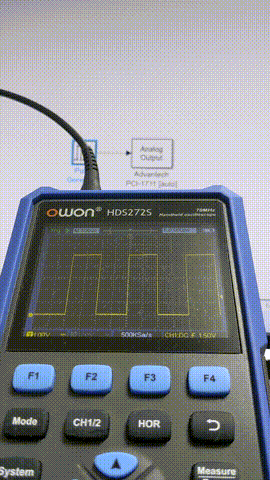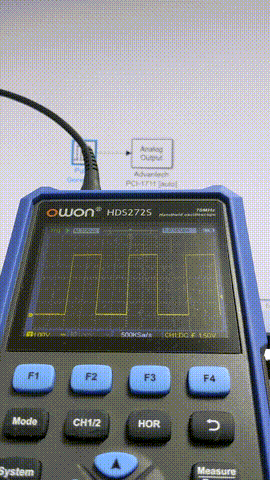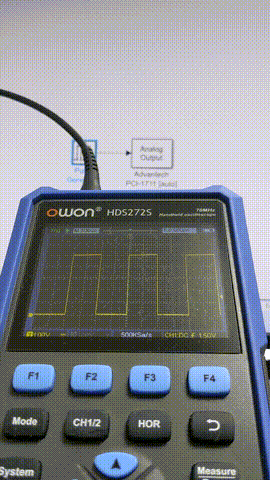
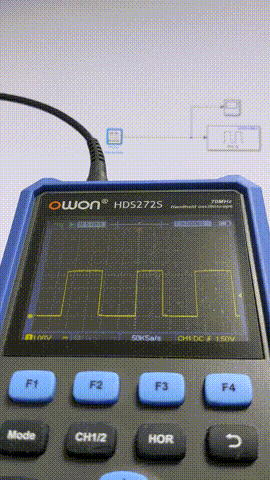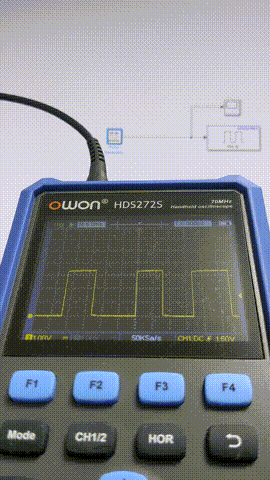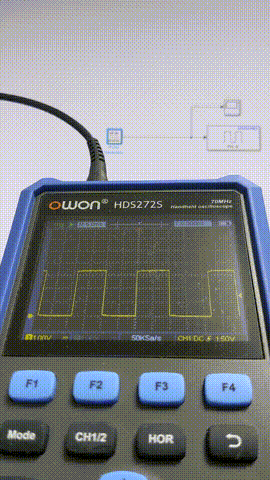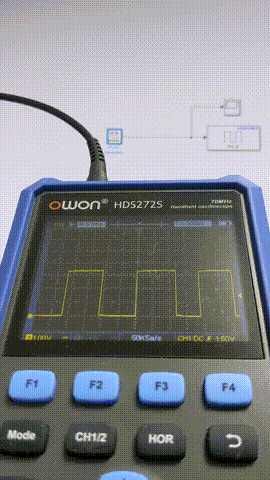
出力波形の確認はOWONのポケットオシロHDS272Sで観測することにしました。DAQより先に据え置きのオシロ買うだろ普通・・・というロジハラ兄貴には「Teamsの日本語変換の第一候補がひらがなになるやつ」が毎回起こる呪いをかけておきます。
10 ms
止まって見えますがGIFアニメです。
5 ms
同上
1 ms
同上
0.5 ms
このあたりからちらほらフレーム欠けが出るようになってきました。
実際にリアルタイム制御などを行う場合、ほかの処理も組み込む必要があるので1 ms～10 msあたりが限界になるでしょうか。
参考：Arduino Due Connected I/O Mode 10 ms
Arduino Dueと比較した場合、Connected I/O Modeだと10 msでもジッタが出ています。
参考：Arduino Due Kernel Mode 0.1 ms
まぁこんなもんKernelモード一強に決まってるんですが。
以上。
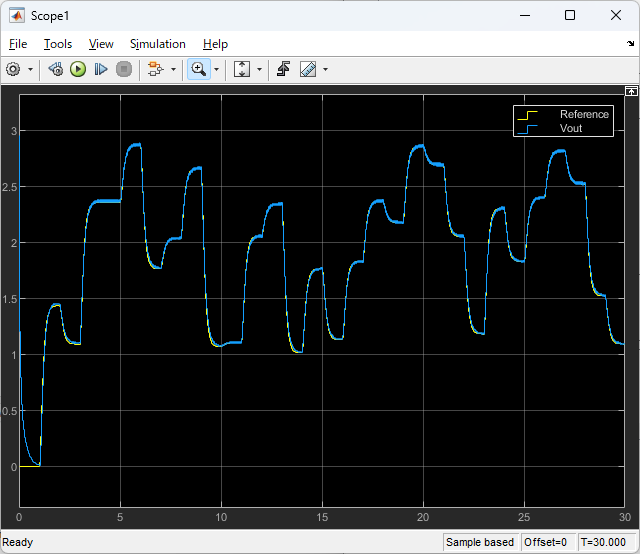
(おまけ)まぁそういうのは置いといて制御がしたいんだよな。
せっかくSimulink側にモデルがあるので、ちょっと複雑な機能を使った制御がしたいです。ここではSystem Identification ToolboxのRecursive Least Square Estimator(逐次最小二乗推定器)を用いてモデル規範型適応制御(MRAC)を試してみましょう。
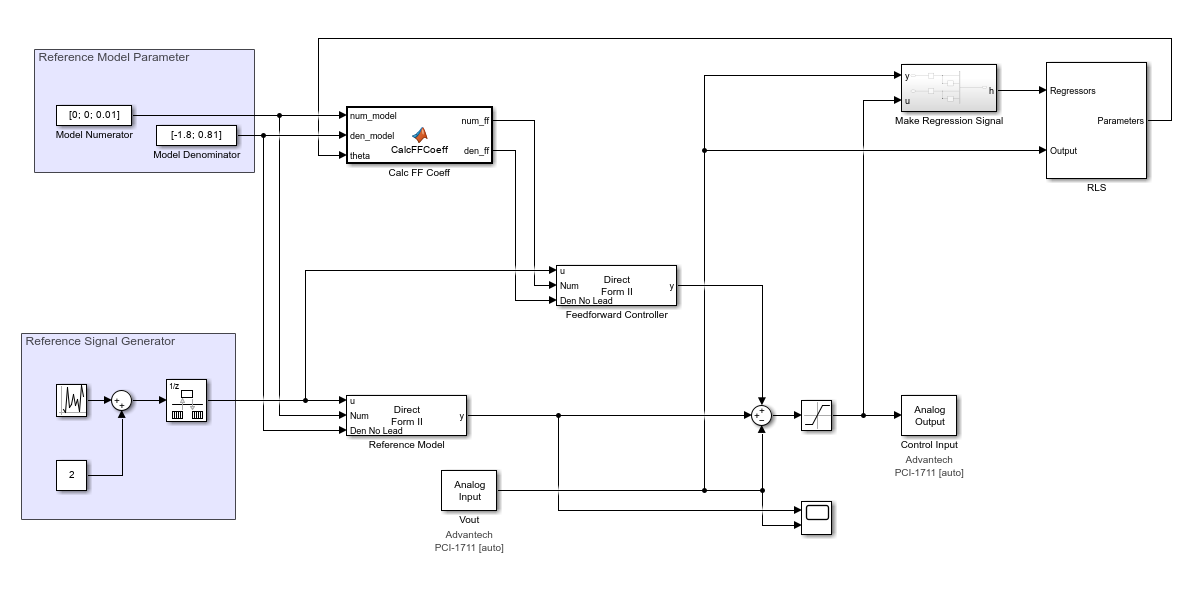
詳細は省きますがこの制御系では制御対象の未知パラメータ最小二乗法で推定し、推定結果に応じて制御器を適応的にチューニングすることで、制御対象の出力を理想応答モデルに追従させます。
- 制御対象
飽きもせず以下の構成の電気回路を使用しています。
Vin-Vout間の伝達関数は2次なので、10 msで離散化した制御対象の構造とパラメータを以下のように定義しました。
$$
P(z)=\frac{b_1 z^{-1}+b_2 z^{-2}}{1+a_1 z^{-1}+a_2 z^{-2}}
$$
- モデル
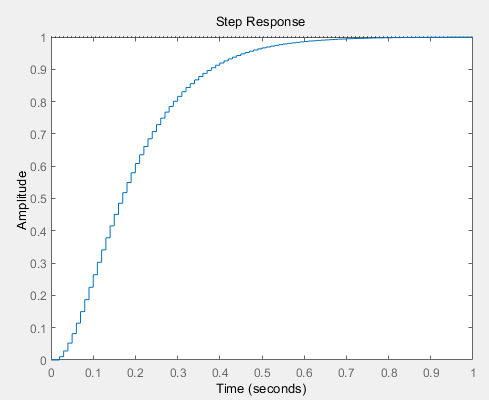
理想応答のモデルは以下の通りです。
$$
W(z)=\frac{0.01 z^{-2}}{1-1.8z^{-1}+0.81 z^{-2}}
$$
- 射影アルゴリズム
$b_{1} < b_{2}$のときには得られる制御器自体が不安定になります。この制御対象では常に$b_{1} > b_{2}$なので線形系で考えればパラメータ推定が進むまで放っておいていいのですが、出力リミットによる非線形性がある場合には上下限張り付きのまま推移してしまう可能性があります。ここでは、図中のMATLAB Functionブロックで制御器のチューニングを行う際に以下の射影アルゴリズムで安定性を担保しています。
\begin{bmatrix}
b_{1}\\
b_{2}
\end{bmatrix}
\leftarrow\frac{b_{1}+b_{2}}{2}\begin{bmatrix}
1\\
1
\end{bmatrix}
% theta = [a1; a2; b1; b2]
function [num_ff, den_ff] = CalcFFCoeff(num_model, den_model, theta)
num_plant = theta(3:4);
% 射影アルゴリズム
if num_plant(1) < num_plant(2)
num_plant = sum(num_plant)*[1; 1]/2;
end
den_plant = [1; -theta(1:2)];
den_ff_temp = conv([1; den_model], num_plant);
% 制御器の伝達関数の分母多項式をモニックにする。
num_ff = [0; conv(den_plant, num_model(end)) / den_ff_temp(1)];
den_ff = den_ff_temp(2:end) / den_ff_temp(1);
end
- 結果
