どうも、待望のエアドロップがベレー帽だった幸福の制御工学です。
概要
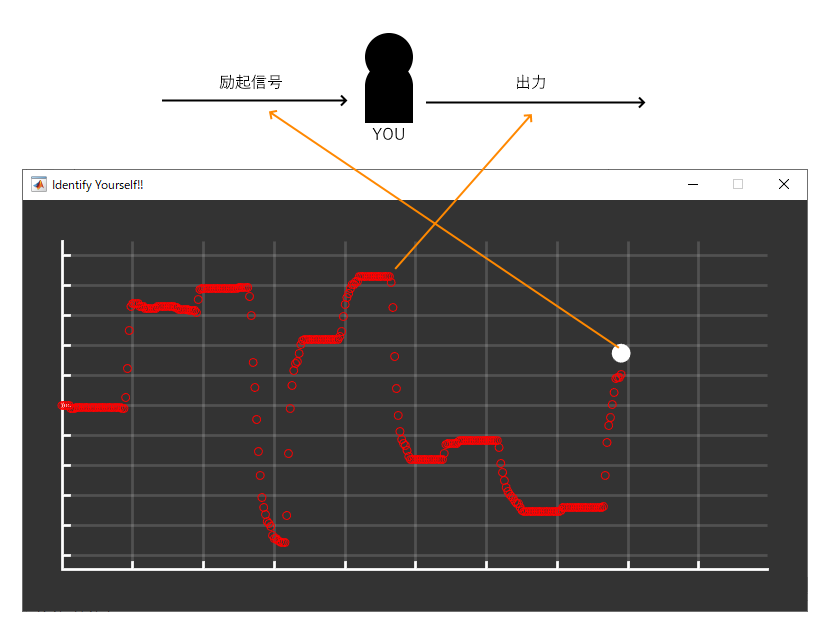
表題の文言を最近知りました。ので、YouをIdentifyするゲーム(?)をMATLABで作りました。
MATLABのプロットウィンドウ上で同定用励起信号をマウス等でトラックすると、あなたの動特性が計算されます。
ダウンロード先
以下のファイルをダウンロードして"ident_you"を実行してください。
ダウンロードリンク
なお、以下の環境を前提としております。
- ご家庭のMATLAB
- PC
- ポインティングデバイス
- System Identification Toolbox(あれば)
コード解説
ここで取ってつけたような解説を書いておきます(Qiitaなので)。今回使用したボタンやらマウス位置取得はすべてMATLABグラフィックスオブジェクトのコールバック機能を用いて実装されています(参考 by @macht氏, MathWorks公式ドキュメント)。
GUIボタン
タイトル画面で励振信号をM系列/ランダムステップで切り替えるボタンはrectangleオブジェクトで実装しています。以下のサンプルコードの通り、rectangleオブジェクトはクリック時にButtonDownFcnで指定されたコールバック関数を呼び出すため、ここにボタンの動作を指定します。なお、デフォルトではPickablePartsプロパティが'visible'に設定されているため、FaceColorプロパティを指定して色を付けるか、PickablePartsプロパティを'all'に指定しないとエッジの部分にのみ「当たり判定」が発生します。
% ボタンの外見指定
pos_x = 0;
pos_y = 0;
width = 5;
height = 2;
color = [0.9, 0.1 0.1];
% クリック時のコールバック関数
OnBtnClicked = @(~,~) disp('Clicked!');
% rectangleを作成
rectangle('Position', [pos_x-width/2, pos_y-height/2, width, height], 'FaceColor', color, 'ButtonDownFcn', OnBtnClicked);
% 表示調整
xlim([-10, 10]);
ylim([-10, 10]);
axes上のマウスポインタ位置の取得
同定実験中にユーザのマウス操作をキャプチャするのにも、figureオブジェクトのWindowButtonMotionFcnコールバックを使用しています。以下のサンプルではさらにコールバック中にaxesオブジェクトのCurrentPointプロパティを参照して、タイトルにポインタ位置を表示しています。
% マウス移動時のコールバック
% 第1引数oは呼び出し元のオブジェクト(hf)
% Childrenで子オブジェクトのhaを参照
OnMouseMove = @(o,~) title(o.Children, string(o.Children.CurrentPoint(1,1:2)));
% figureオブジェクト
hf = figure('WindowButtonMotionFcn', OnMouseMove);
% axesオブジェクト
ha = axes(hf);
% 飾り
scatter(ha, rand(10, 1), rand(10, 1));
補遺
- System Identificaton Toolboxが導入されている環境では入力むだ時間推定付きのarx、導入されていなければ自前の最小二乗法で同定を行います。
- Toolboxの導入状況によらず、モデル次数はともに3としています。これは事前実験でN4SIDによる次数推定結果が概ね3となったためです。
- 実応用上でも、Human in the loopな制御系においてはユーザのモデルを考えることは有用です。(Hidden Oscillations In The Closed-Loop Aircraft-Pilot System And Their Prevention)