離散時間代数Riccati方程式

概要

何年か前にRiccatiソルバを書いたときのメモです。

元論文

• Alan J. Laub, "A SCHUR METHOD FOR SOLVING ALGEBRAIC RICCATI EQUATIONS" (1978)
• T. Pappas, A. J. Laub, N. R. Sandell, Jr., "On the Numerical Solution of the Discrete Time Algebraic Riccati Equation" (1979)

離散時間代数Riccati方程式

行列$P\in\mathbb{R}^{n\times n}$を未知数とする行列方程式(1)を離散時間代数Riccati方程式(DARE: Discrete-time Algebraic Riccati Equation)といいます。

    P = A^\mathsf{T}PA-A^\mathsf{T}PB\left(R+B^\mathsf{T}PB\right)^{-1}B^\mathsf{T}PA+Q \tag{1}

    A\in\mathbb{R}^{n\times n}, B\in\mathbb{R}^{n\times m}, Q\in\mathbb{R}^{n\times n}, R\in\mathbb{R}^{m\times m}

ただし、各行列について以下の仮定をおきます。

• $Q$は半正定対称行列$\left(Q=Q^\mathsf{T}\succeq0\right)$
• $R$は正定対称行列$\left(R=R^\mathsf{T}\succ0\right)$
• 対$(A,B)$は可安定
• 対$(Q^{1/2},A)$は可検出

解法

離散時間動的Riccati方程式の反復による解法

離散時間Riccati方程式のバリエーションとして、離散時間動的Riccati方程式(DDRE: Discrete-time Dynamic Riccati Equation)があります。

    P_{k-1} = A^\mathsf{T}P_{k}A-A^\mathsf{T}P_{k}B\left(R+B^\mathsf{T}P_{k}B\right)^{-1}B^\mathsf{T}P_{k}A+Q \tag{2}

$P_{k-1}=P_{k}=P$とすればDDREはDARE(1)に一致するため、適当な行列$P_0$を初期解としてDDRE(2)を更新し続けることで、定常状態$P_{k-1}\approx P_{k}$においてDARE(1)の解$P\approx P_k$を得ることができます。

しかしこの方法は、収束度合いが(2)のダイナミクスに支配されており、係数行列によっては収束が遅くなります。

行列分解による解法

そこで本稿では、より効率的なアルゴリズムとして、実Schur分解/実QZ分解に基づく解法を解説します。まず、DDRE(2)が適当な変換により線形な漸化式へ帰着できることを示します。次に、係数行列$A$の可逆性を仮定した実Schur分解による解法、さらにその仮定を除いた実QZ分解による解法を解説します。

DDREの線形漸化式への変換

反復計算によらずDDREを解くため、仮に適当な行列$H$を用いてDDREを

    P_{k-1}=HP_{k}

と表せたとすると、$H$の固有値に注目することで極限値

\lim_{k\to-\infty}P_k

を求められそうです。しかしDDREは非線形であるためこのような表現ができません。そこで、次の変数変換

    P_k=:N_kM_k^{-1}, N_k\in\mathbb{R}^{n\times n}, M_k\in\mathbb{R}^{n\times n}

を考えます。この変数変換により、

DDREは以下の漸化式

\left[\begin{array}{cc}I_{n}&G\O&A^\mathsf{T}\end{array}\right]\left[\begin{array}{cc}M_k\N_k\end{array}\right]=\left[\begin{array}{cc}A&O\-Q&I_n\end{array}\right]\left[\begin{array}{cc}M_{k-1}\N_{k-1}\end{array}\right]\tag{3}

>
> へと変換されます。ただし、$G:=BR^{-1}B^\mathsf{T}$で、$I_n$は$n$次の単位行列です。
>
> **証明**
> (3)より以下の2本の連立方程式を考える。

> ``` math
    \left\{
    \begin{array}{rcl}
        M_k+GN_k&=&AM_{k-1}\\
        A^\mathsf{T}N_k&=&-QM_{k-1}+N_{k-1}
    \end{array}
    \right.

第1式より

\begin{aligned}
    M_k+GN_k&=AM_{k-1}\\
    \Rightarrow \left(I_n+GN_kM_k^{-1}\right)M_k&=AM_{k-1}\\
    \Rightarrow M_{k-1}^{-1}&=M_k^{-1}\left(I_n+BR^{-1}B^\mathsf{T}P_k\right)^{-1}A
\end{aligned}

> であり、括弧内を逆行列補題を用いて整理すると
> 
> ``` math
    \begin{aligned}
        \left(I_n+BR^{-1}B^\mathsf{T}P_k\right)^{-1} &= I_n^{-1}-I_n^{-1}B\left(R+B^\mathsf{T}P_kI_n^{-1}B\right)^{-1}B^\mathsf{T}P_kI_n^{-1}\\
        &= I_n-B\left(R+B^\mathsf{T}P_kB\right)^{-1}B^\mathsf{T}P_k\\
        \Rightarrow M_{k-1}^{-1}&=M_k^{-1}\left(I_n-B\left(R+B^\mathsf{T}P_kB\right)^{-1}B^\mathsf{T}P_k\right)A
    \end{aligned}

を得る。第2式より

\begin{aligned}
    A^\mathsf{T}N_k&=-QM_{k-1}+N_{k-1}\\
    \Rightarrow A^\mathsf{T}N_kM_{k-1}^{-1}+Q&=N_{k-1}M_{k-1}^{-1}\\
    &=P_{k-1}
\end{aligned}

> であるため、第1式の結果と併せてDDRE(2)が得られる。
>
> ``` math
    \begin{aligned}
        P_{k-1} &= A^\mathsf{T}N_kM_{k-1}^{-1}+Q\\
        &= A^\mathsf{T}N_kM_k^{-1}\left(I_n-B\left(R+B^\mathsf{T}P_kB\right)^{-1}B^\mathsf{T}P_k\right)A+Q\\
        &= A^\mathsf{T}P_k\left(I_n-B\left(R+B^\mathsf{T}P_kB\right)^{-1}B^\mathsf{T}P_k\right)A+Q\\
        &= A^\mathsf{T}P_{k}A-A^\mathsf{T}P_{k}B\left(R+B^\mathsf{T}P_{k}B\right)^{-1}B^\mathsf{T}P_{k}A+Q
    \end{aligned}

実Schur分解による解法

漸化式(3)において、さらに行列$A$の可逆性を仮定した場合、左辺の係数行列には逆行列が存在し、以下の漸化式(4)が得られます。

\begin{aligned}
\left[\begin{array}{cc}M_k\\N_k\end{array}\right]&=\left[\begin{array}{cc}I_{n}&G\\O&A^\mathsf{T}\end{array}\right]^{-1}\left[\begin{array}{cc}A&O\\-Q&I_n\end{array}\right]\left[\begin{array}{cc}M_{k-1}\\N_{k-1}\end{array}\right]\\
&=\left[\begin{array}{cc}I_{n}&G\\O&A^\mathsf{T}\end{array}\right]\left[\begin{array}{cc}A&O\\-Q&I_n\end{array}\right]\left[\begin{array}{cc}M_{k-1}\\N_{k-1}\end{array}\right]\\
&=\left[\begin{array}{cc}A+GA^{-\mathsf{T}}Q&-GA^{-\mathsf{T}}\\-A^{-\mathsf{T}}Q&A^{-\mathsf{T}}\end{array}\right]\left[\begin{array}{cc}M_{k-1}\\N_{k-1}\end{array}\right]
\end{aligned}\tag{4}

ここで、$A^{-\mathsf{T}}=\left(A^\mathsf{T}\right)^{-1}$です。(4)の係数行列を新たに

    H:=\left[\begin{array}{cc}A+GA^{-\mathsf{T}}Q&-GA^{-\mathsf{T}}\\-A^{-\mathsf{T}}Q&A^{-\mathsf{T}}\end{array}\right]\in\mathbb{R}^{2n\times 2n}

とおき、この漸化式の極限値を求めるために$H$の固有値に注目すると、

$H$の$2n$個の固有値のうち、$n$個は絶対値が1未満、残る$n$個は絶対値が1より大きいことが示せます。

証明
行列

J:=\left[
    \begin{array}{cc}
        O&I_n\\
        -I_n&O
    \end{array}
    \right] \in \mathbb{R}^{2n\times 2n}

> に対し、$H$は
> 
> ``` math
    H^{-1}=J^{-1}H^\mathsf{T}J

を満たす(このような行列をシンプレクティック行列という)。いま、$H$の固有値の集合を$\sigma(H)$とするとき、転置により固有値は不変のため、

\lambda \in \sigma(H) \Leftrightarrow\lambda\in\sigma\left(H^\mathsf{T}\right)

> である。$H^\mathsf{T}$の固有方程式を考えると、
> 
> ``` math
    \begin{aligned}
        \det\left(\lambda I_{2n}-H^\mathsf{T}\right) &= \det\left(\lambda JJ^{-1}-H^\mathsf{T}\right)\\
        &= \det\left(J\left(\lambda I_{2n}-J^{-1}H^\mathsf{T}J\right)J^{-1}\right)\\
        &= \det\left(J\right)\det\left(\lambda I_{2n}-J^{-1}H^\mathsf{T}J\right)\det\left(J^{-1}\right)\\
        &= \det\left(J\right)\det\left(\lambda I_{2n}-H~^{-1}\right)\det\left(J^{-1}\right)\\
        &=0
    \end{aligned}

を得るが、$J$が正則であるため上式は

\det\left(\lambda I_{2n}-H~^{-1}\right) = 0

> を意味する。これは$H^{-1}$の固有方程式であり、従って
> 
> ``` math
    \lambda\in\sigma\left(H\right) \Rightarrow \lambda\in\sigma\left(H^{-1}\right)

がいえる。任意の正則行列に対し、逆行列の固有値はもとの行列の固有値の逆数であるため、

\lambda\in\sigma\left(H^{-1}\right) \Leftrightarrow \lambda^{-1}\in\sigma\left(H\right)

> がいえ、
> 
> ``` math
    \lambda\in\sigma\left(H\right) \Rightarrow \lambda^{-1}\in\sigma\left(H\right)

である。上式は$H$の固有値は絶対値が1未満のものと1より大きいものの対になっているか、あるいは絶対値が1で重複しているかのいずれかであることを意味する。しかし、各係数行列に関する仮定により絶対値が1の固有値は存在しないことが以下の通り示される。

背理法により絶対値が1の固有値が存在すると仮定し矛盾を導く。つまり、ある$\lambda\in\sigma(H)$について、

\lambda\bar{\lambda}=1

> とする。$\lambda$に対応する固有ベクトルを$v\in\mathbb{C}^{2n}$とおき、
> 
> ``` math
    v = \left[
            \begin{array}{c}
                v_1\\v_2
            \end{array}
        \right],v_1\in\mathbb{C}^n,v_2\in\mathbb{C}^n

とする。従って、

\begin{aligned}
    Hv &= \lambda v\\
    \left[\begin{array}{cc}A+GA^{-\mathsf{T}}Q&-GA^{-\mathsf{T}}\\-A^{-\mathsf{T}}Q&A^{-\mathsf{T}}\end{array}\right]\left[
        \begin{array}{c}
            v_1\\v_2
        \end{array}
    \right]&=\lambda\left[
        \begin{array}{c}
            v_1\\v_2
        \end{array}
    \right]
\end{aligned}

> である。第2行に左から$G$を掛けて第1行に加えることで
> 
> ``` math
    Av_1=\lambda v_1 + \lambda Gv_2

が、第2行を$Qv_1$について解いて

Qv_1=v_2-\lambda A^\mathsf{T}v_2

> がそれぞれ得られる。これらより、
> 
> ``` math
    \left\{
        \begin{array}{rcl}
            \bar{\lambda}v_2^*Av_1&=&\lambda\bar{\lambda}v_2^*v_1+\lambda\bar{\lambda}v_2^*Gv_2\\
            v_1^*Qv_1&=&v_2^*v_1-\bar{\lambda}v_2^*Av_1
        \end{array}
    \right.\\
    \Rightarrow v_1^*Qv_1=-v_2^*Gv_2

である。$Q,G=BR^{-1}B^\mathsf{T}$は共に半正定、$R$は正定であるため、これは

Q^{1/2}v_1=B^\mathsf{T}v_2=0

> を意味する。以上より、
> 
> ``` math
    \begin{aligned}
        \left[
            \begin{array}{c}
                A-\lambda I \\ Q^{1/2}
            \end{array}
        \right]v_1 &= 0\\
        v_2^*\left[
            \begin{array}{cc}
                A^\mathsf{T}-\lambda^{-1} I & B
            \end{array}
        \right] &= 0\\
    \end{aligned}

が得られるが、$v$は固有ベクトルであるため$v_1,v_2$の少なくとも一方は非零ベクトルである。すなわち

    \left[
        \begin{array}{c}
            A-\lambda I \\ Q^{1/2}
        \end{array}
    \right],\left[
        \begin{array}{cc}
            A^\mathsf{T}-\lambda^{-1} I & B
        \end{array}
    \right]

> の片方または両方が、$\lvert\lambda\rvert= \lvert\lambda^{-1}\rvert=1$に対しランク落ちすることを意味し、可安定性または可検出性の仮定に反する(PBHテスト)。
> 
> 以上より、$H$の固有値のうち、$n$個の絶対値は1より大きく、残る$n$個の絶対値は1未満である。

### 実Schur分解によるDAREの解法
まず実Schur分解について説明します。任意の実正方行列$X\in\mathbb{R}^{n\times n}$に対して、以下を満足する直交行列$U\in\mathbb{R}^{n\times n}$が存在します。
 - $U^\mathsf{T}XU$がブロック上三角行列となる
 - $U^\mathsf{T}XU$のブロック対角要素には、$X$の実固有値、または$X$の複素共役な2つの固有値をもつ$2\times 2$行列を任意の順序で並べられる

たとえば、行列

``` math
    X=\left[
        \begin{array}{cccc}
            2&2&0&-1\\
            3&3&0&5\\
            3&2&1&4\\
            0&-2&0&3
        \end{array}
        \right]

は固有値$1,3\pm j2,2$を持ち、直交行列

    U=\left[
        \begin{array}{cccc}
            0&1/\sqrt{2}&0&1/\sqrt{2}\\
            0&0&1&0\\
            1&0&0&0\\
            0&-1/\sqrt{2}&0&1/\sqrt{2}
        \end{array}
        \right]

により

    U^\mathsf{T}XU = \left[
        \begin{array}{c|cc|c}
            1&-1/\sqrt{2}&2&7/\sqrt{2}\\\hline
            0&3&2\sqrt{2}&-1\\
            0&-\sqrt{2}&3&4\sqrt{2}\\\hline
            0&0&0&2
        \end{array}
        \right]

と分解されます。ブロック対角要素の固有値はそれぞれ$1,3\pm j2,2$です。この分解を実Schur分解と呼びます。

$H$に対し実Schur分解を適用すると、

    U^\mathsf{T}HU=\left[\begin{array}{cc}H_{11}&H_{12}\\O&H_{22}\end{array}\right]

において$H_{11}$のブロック対角要素の固有値が$H$の固有値のうち絶対値が1未満の$n$個、$H_{22}$のブロック対角要素の固有値が1より大きい$n$個となるように分解することができます。

    H=U\left[\begin{array}{cc}H_{11}&H_{12}\\O&H_{22}\end{array}\right]U^\mathsf{T}

を漸化式(4)に代入すると、

\begin{aligned}
\left[\begin{array}{cc}M_k\\N_k\end{array}\right]&=H\left[\begin{array}{cc}M_{k-1}\\N_{k-1}\end{array}\right]\\
&= U\left[\begin{array}{cc}H_{11}&H_{12}\\O&H_{22}\end{array}\right]U^\mathsf{T}\left[\begin{array}{cc}M_{k-1}\\N_{k-1}\end{array}\right]\\
\Rightarrow U^\mathsf{T}\left[\begin{array}{cc}M_k\\N_k\end{array}\right]&= \left[\begin{array}{cc}H_{11}&H_{12}\\O&H_{22}\end{array}\right]U^\mathsf{T}\left[\begin{array}{cc}M_{k-1}\\N_{k-1}\end{array}\right]
\end{aligned}

となります。簡単のため、$U$を$n\times n$のブロックに分割し

    U=\left[\begin{array}{cc}U_{11}&U_{12}\\U_{21}&U_{22}\end{array}\right]

とおき、変数変換

    \begin{aligned}
        \left[\begin{array}{c}\tilde{M}\\\tilde{N}\end{array}\right] &:= U^\mathsf{T}\left[\begin{array}{c}M\\N\end{array}\right]\\
        &:= \left[
            \begin{array}{c}
                U_{11}^\mathsf{T}M+U_{21}^\mathsf{T}N\\U_{12}^\mathsf{T}M+U_{22}^\mathsf{T}N
            \end{array}
            \right]
    \end{aligned}

を施すと、

\begin{aligned}
\left[\begin{array}{c}\tilde{M}_k\\\tilde{N}_k\end{array}\right]&= \left[\begin{array}{cc}H_{11}&H_{12}\\O&H_{22}\end{array}\right]\left[\begin{array}{c}\tilde{M}_{k-1}\\\tilde{N}_{k-1}\end{array}\right]
\end{aligned}

が得られます。ここで、ブロック行列の第2行目に着目すると

    \tilde{N}_{k}=H_{22}\tilde{N}_{k-1}

です。$H_{22}$のブロック対角要素の固有値は1より大きく、ブロック上三角行列の固有値はブロック対角要素の固有値に等しいため$H_{22}$は正則かつ$H_{22}^{-1}$はSchur安定です。以上より漸化式

    \tilde{N}_{k-1}=H_{22}^{-1}\tilde{N}_{k}

について

    \tilde{N}_{-\infty}:=\lim_{k\to-\infty}\tilde{N}_k=O

が成立し。変数をもとに戻すと、

    \tilde{N}_{-\infty}=U_{12}^\mathsf{T}M_{-\infty}+U_{22}^\mathsf{T}N_{-\infty}=O

となります。これにより、DARE(1)の解が

    \begin{aligned}
        P&=\lim_{k\to-\infty}P_{-k}\\
        &=N_{-\infty}M_{-\infty}^{-1}\\
        &=-U_{22}^{-\mathsf{T}}U_{12}^\mathsf{T}
    \end{aligned}

で構成されます。

実QZ分解による解法

前項では係数行列$A$の正則性を仮定しましたが、$A$が特異な場合、

    \left[\begin{array}{cc}I_{n}&G\\O&A^\mathsf{T}\end{array}\right]^{-1}

が定義できず、行列$H$を構成できません。そこで、両辺の係数行列を維持したまま漸化式(3)を解きます。このために用いられるのが一般化固有値と実QZ分解です。

一般化固有値

与えられた正方行列$E,F$に対し、スカラ$\lambda$および非零ベクトル$v$が存在し、

    Ev=\lambda Fv

なる関係が成り立つとき、$\lambda$を一般化固有値、$v$を一般化固有ベクトルといいます。いま、

    \begin{aligned}
        E &:= \left[\begin{array}{cc}A&O\\-Q&I_n\end{array}\right]\\
        F &:= \left[\begin{array}{cc}I_n&G\\O&A^\mathsf{T}\end{array}\right]
    \end{aligned}

とおくとき、$E,F$の一般化固有値について

$E,F$の$2n$個の一般化固有値のうち、$n$個は絶対値が1未満、残る$n$個は絶対値が1より大きいことが示せます。

証明
$\lambda$を$E,F$の一般化固有値とする。

\det(E-\lambda F)=\det\left(E^\mathsf{T}-\lambda F^\mathsf{T}\right)

>より、通常の固有値と同様、一般化固有値も転置により不変である。従って、$E^\mathsf{T},F^\mathsf{T}$に対して一般化固有値$\lambda$に属する適当な一般化固有ベクトル$w\neq0$が存在し、
>
>``` math
    E^\mathsf{T}w=\lambda F^\mathsf{T}w

が成り立つ。両辺に左から$FJ$を掛けると、$E,F$の定義より、$FJF^\mathsf{T}=EJE^\mathsf{T}$なので、

\begin{aligned}
FJE^\mathsf{T}w&=\lambda FJF^\mathsf{T}w\\
&=\lambda EJE^\mathsf{T}w
\end{aligned}

>を得る。$JE^\mathsf{T}w$を新たな一般化固有ベクトルとみなせば
>
>``` math
\begin{aligned}
    F\left(JE^\mathsf{T}w\right)&=\lambda E\left(JE^\mathsf{T}w\right)\\
    \Rightarrow E\left(JE^\mathsf{T}w\right)&=\lambda^{-1} F\left(JE^\mathsf{T}w\right)
\end{aligned}

より$\lambda^{-1}$も$E,F$の一般化固有値であることがわかる。さらに$\lambda$の絶対値が1ではないことは$H$の固有値の場合と同様に証明できる。

実QZ分解によるDAREの解

次に実QZ分解(一般化実Schur分解)について説明します。任意の実正方行列$E,F$に対して、以下を満足する直交行列$Q,Z$が存在します。

• $Q^\mathsf{T}EZ,Q^\mathsf{T}FZ$がともにブロック上三角行列となる。
• $Q^\mathsf{T}EZ,Q^\mathsf{T}FZ$の$i$番目のブロック対角要素$\left(Q^\mathsf{T}EZ\right)_i,\left(Q^\mathsf{T}FZ\right)_i$には、比
  $\left(Q^\mathsf{T}EZ\right)_i\left(Q^\mathsf{T}FZ\right)_i^{-1}$が$E,F$の実一般化固有値または複素共役な一般化固有値対を持つ$2\times 2$行列を任意の順序で並べたものとなるように設定できる。

$E,F$に実QZ分解を施すことで、

    \begin{aligned}
        Q^\mathsf{T}EZ&=\left[
                \begin{array}{cc}
                    E_{11}&E_{12}\\
                    O&E_{22}
                \end{array}
            \right]\\
        Q^\mathsf{T}FZ&=\left[
                \begin{array}{cc}
                    F_{11}&F_{12}\\
                    O&F_{22}
                \end{array}
            \right]
    \end{aligned}

において$E_{22}F_{22}^\mathsf{-1}$の固有値が$E,F$の一般化固有値のうち絶対値が1より大きな$n$個となるように分解できます。

    \begin{aligned}
        E&=Q\left[
                \begin{array}{cc}
                    E_{11}&E_{12}\\
                    O&E_{22}
                \end{array}
            \right]Z^\mathsf{T}\\
        F&=Q\left[
                \begin{array}{cc}
                    F_{11}&F_{12}\\
                    O&F_{22}
                \end{array}
            \right]Z^\mathsf{T}
    \end{aligned}

をもとの漸化式に代入し、変数変換

    Z^\mathsf{T}\left[\begin{array}{c}M\\N\end{array}\right]=\left[\begin{array}{c}\tilde{M}\\\tilde{N}\end{array}\right]

を導入することで、

    \begin{aligned}
        F\left[\begin{array}{c}M_k\\N_k\end{array}\right]&=E\left[\begin{array}{c}M_{k-1}\\N_{k-1}\end{array}\right]\\
        \Rightarrow Q\left[
                \begin{array}{cc}
                    F_{11}&F_{12}\\
                    O&F_{22}
                \end{array}
            \right]Z^\mathsf{T}\left[\begin{array}{c}M_k\\N_k\end{array}\right]&=Q\left[
                \begin{array}{cc}
                    E_{11}&E_{12}\\
                    O&E_{22}
                \end{array}
            \right]Z^\mathsf{T}\left[\begin{array}{c}M_{k-1}\\N_{k-1}\end{array}\right]\\
            \Rightarrow \left[
                \begin{array}{cc}
                    F_{11}&F_{12}\\
                    O&F_{22}
                \end{array}
            \right]Z^\mathsf{T}\left[\begin{array}{c}M_k\\N_k\end{array}\right]&=\left[
                \begin{array}{cc}
                    E_{11}&E_{12}\\
                    O&E_{22}
                \end{array}
            \right]Z^\mathsf{T}\left[\begin{array}{c}M_{k-1}\\N_{k-1}\end{array}\right]\\
            \Rightarrow \left[
                \begin{array}{cc}
                    F_{11}&F_{12}\\
                    O&F_{22}
                \end{array}
            \right]\left[\begin{array}{c}\tilde{M}_k\\\tilde{N}_k\end{array}\right]&=\left[
                \begin{array}{cc}
                    E_{11}&E_{12}\\
                    O&E_{22}
                \end{array}
            \right]\left[\begin{array}{c}\tilde{M}_{k-1}\\\tilde{N}_{k-1}\end{array}\right]
    \end{aligned}

を得ます。実Schur分解の場合と同様に、$\tilde{N}$に関して

    \tilde{N}_{k-1}=E_{22}^{-1}F_{22}\tilde{N}_{k}

のため、仮定より$E_{22}^{-1}F_{22}$の固有値は1未満なので、

    \tilde{N}_{-\infty}=\lim_{k\to-\infty}\tilde{N}_k=Z_{12}^\mathsf{T}M_{-\infty}+Z_{22}^\mathsf{T}N_{-\infty}=O

であり、DAREの解が

    P=N_{-\infty}M_{-\infty}^{-1}=-Z_{22}^{-\mathsf{T}}Z_{12}^\mathsf{T}

で構成されます。

実装例

JuliaにてDDREの反復による方法と、実QZ分解を用いた方法を実装してみます。環境はMicrosoft Surface Notebook2/Ubuntu 20.04.1 LTS上のJulia1.5.2です。

DDRE(2)を実装すると以下のようになります。ただし高速化のため右辺の行列$A$に関する乗算をくくりだしています。

DDREの反復

function dare_ddre(A,B,Q,R,itar)
    P = Q;

    for i in 1:itar
        P = transpose(A)*(P-P*B/(R+transpose(B)*P*B)*transpose(B)*P)A+Q;
    end

    return P;
end

次に実QZ分解を用いたコードは以下の通りです。JuliaではLinearAlgebra.jlのschur関数が実Schur分解、実QZ分解双方をサポートしています。ただしschur関数は絶対値が1未満の固有値を右下ブロックに集めるように分解を行うため、ordschur関数で並べ替えを行います。

実QZ分解

function dare_qz(A, B, Q, R)
    n = size(A, 1);

    E = [
        Matrix{Float64}(I, n, n) B*(R\B');
        zeros(size(A)) A'
    ];
    F = [
        A zeros(size(A));
        -Q Matrix{Float64}(I, n, n)
    ];

    QZ = schur(F, E);
    QZ = ordschur(QZ, abs.(QZ.alpha./QZ.beta) .< 1);

    return QZ.Z[(n+1):end, 1:n]/QZ.Z[1:n, 1:n];
end

以下、

\begin{aligned}
   A&=\begin{bmatrix}0&1&0\\
1&0&0\\
0&1&1
\end{bmatrix}\\
B&=\begin{bmatrix}
0\\
1\\
0
\end{bmatrix}\\
Q&=I_3\\
R&=1000
\end{aligned}

についてDARE(1)を解きます。次のコードを作成しました。

数値例

using Plots;
using LinearAlgebra;

## 残差を求める無名関数
res(A,B,Q,R,P) = transpose(A)*(P-P*B/(R+transpose(B)*P*B)*transpose(B)*P)A+Q-P;

## DDREの反復による解
function dare_ddre(A,B,Q,R, itar)
    P = Q;

    for i in 1:itar
        P = transpose(A)*(P-P*B/(R+transpose(B)*P*B)*transpose(B)*P)A+Q;
    end

    return P;
end

## 上記の1反復ごとの残差を出力するバージョン
function dare_ddre_err(A,B,Q,R, itar)
    P = Q;

    err = zeros(itar, 1);

    for i in 1:itar
        P = transpose(A)*(P-P*B/(R+transpose(B)*P*B)*transpose(B)*P)A+Q;
        err[i] = norm(res(A,B,Q,R,P));
    end

    return P, err;
end

## 実QZ分解による解
function dare_qz(A, B, Q, R)
    n = size(A, 1);

    E = [
        Matrix{Float64}(I, n, n) B*(R\B');
        zeros(size(A)) A'
    ];
    F = [
        A zeros(size(A));
        -Q Matrix{Float64}(I, n, n)
    ];

    QZ = schur(F, E);

    ## 左上ブロックの一般化固有値が絶対値1未満となるように並べ替え
    QZ = ordschur(QZ, abs.(QZ.alpha./QZ.beta) .< 1);

    return QZ.Z[(n+1):end, 1:n]/QZ.Z[1:n, 1:n];
end

## 係数行列
A = [0 1 0;1 0 0; 0 1 1]
B = [0; 1; 0]
Q = diagm(0 => [1,1,1])
R = 1000

# 時間計測用の繰り返し回数
itar = 1000;
## DDREの反復回数
itar_ddre = 500;

## 実QZ分解の所要時間を記録
buf_time = @elapsed for i in 1:itar
    dare_qz(A,B,Q,R);
end
t_qz = buf_time / itar;

## DDREの1反復あたりの所要時間を計測
buf_time = @elapsed for i in 1:itar
    dare_ddre(A,B,Q,R,itar_ddre);
end
t_dr = buf_time / itar / itar_ddre;

## 実QZ分解による解とその残差
P_qz = dare_qz(A,B,Q,R);
er_qz = norm(res(A,B,Q,R,P_qz));

## DDREの反復による解と各反復における残差
P_dr, er_dr = dare_ddre_err(A,B,Q,R,itar_ddre);

plot((1:length(er_dr))*t_dr, er_dr, yscale=:log10, label=:"DDRE");
scatter!([t_qz], [er_qz], label=:"QZ");
xlabel!("time [s]");
ylabel!("error(2-norm)");

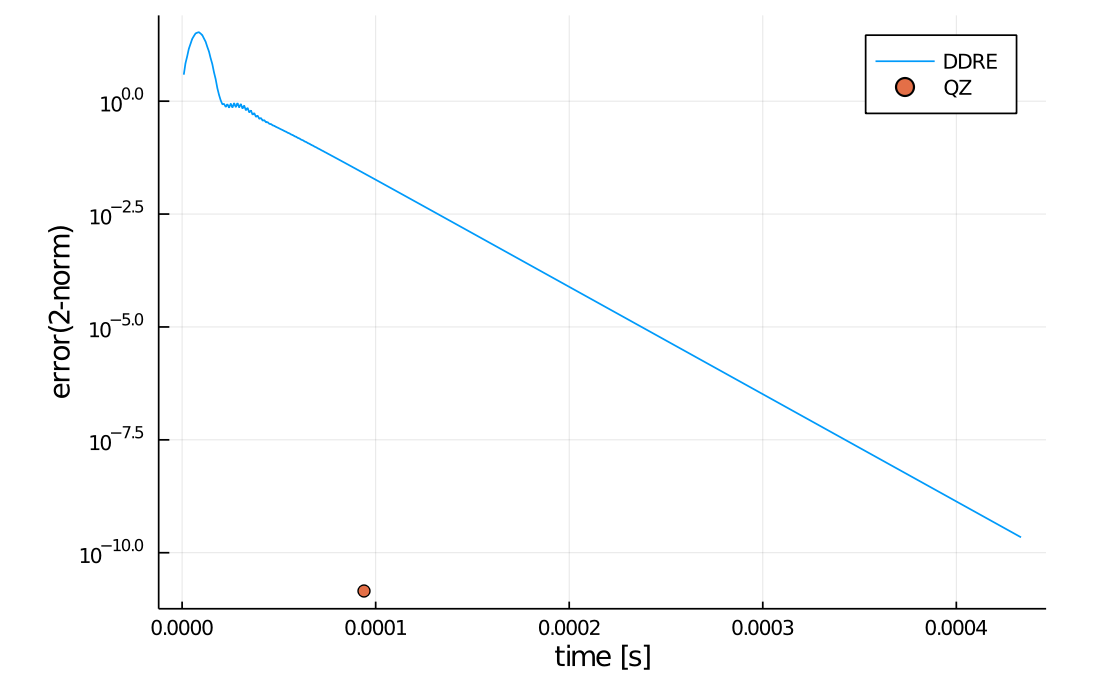
DDRE、実QZ分解ともに1000回の平均を処理時間とし、DDREはさらに反復計算の回数で割って1反復あたりの時間を算出しています。DDREの反復ごとの残差ノルムと、実QZ分解の残差ノルムは以下の図のようになり、DDREの収束が遅い問題に関しては実QZ分解のほうが高速に解を求められることを確認しました。

ちな

飲み屋にイタリア人のおっちゃんがいたので"Riccati"を発音してもらった。
｢リッカーティ｣だった。

— LQGレギュレータの保証された安定余裕 (@HppyCtrlEngnrng) April 10, 2018