動機
KeresでSeq2Seqの実装を進めるうちに、Attention機構を使ってみたいなと思うようになりました。しかし、一筋縄ではいかないようで、その調査と解決に取り組んでみました。
概要
○現状
・Kerasの仕様上、時間軸方向に優先して計算が展開されるので、ある時刻の出力を次の時刻の入力に用いることは(デフォルトでは)できない
・Teacher Forcingを使えば、各時刻の(理想的な)出力を次の時刻の入力に与えられる
・しかしAttentionとなると、Bahdanau et.al(2015)のようなAttentionの実装は難しい
・以下のようなことは、まだ自分にはできなかった
ー自作RNNセルを定義
ー在野の賢人のモジュールの改良
○方針
・自分の手の届く範囲で、うまく実装できないか?
・Luong et.al(2015)の手法ならば、実装できる気がするので、やってみた
課題1 - 時刻tの出力を時刻t+1の入力とできるか
以前自分で書いた記事で、Kerasの実装例に見られる簡単なEncoder-Decoderネットワークの概略を図示したのですが、よくよく考えてみると、Encoder-Decoderネットワーク、Seq2Seqといった界隈で一般的に行われている、
”時刻tのDecoder出力を時刻t+1のDecoder入力に用いる”
ということは行われていないのでした。
上記のことをやりたくて調べていた結果、出会ったのはGithubでの議論です。
ページを半分ほどスクロールしたところにあるmbollmannさんの投稿によると、
”The reason is that to use the output of the current timestep as input for the next one, you would basically need to go "depth-first", i.e., calculate one timestep for ALL layers, then the next timestep, and so on. What Keras does, however, is calculate ALL timesteps of ONE layer, before feeding the output into the next one."
はしょりつつ要点を挙げると、
・現在の時刻の出力を次の時刻の入力に使いたい場合は、”深さ優先”計算、つまり、ある時刻で全ての層について計算を行って、その後に次の時刻に進むことが必要
・しかしながら、Kerasは一つの層について全ての時刻を(先に)計算する
ということです。
残念...と思っていたのですが、RNNの学習を促進させるための手法として、Teacher Forcingというものが知られています。これは、時刻tの出力を時刻t+1の入力にするのではなく、時刻tのGround Truthを時刻t+1の入力にしてしまおう、という手法です。
学習途中では、各時刻の出力と教師出力に差が大きいため、それを毎時刻入力してしまうとどんどん誤差が蓄積しますが、この手法なら少なくとも入力はいつも理想的なので、収束は進みそうですよね。
さらに実装面でも、教師出力を入力すればいいだけなので、ありがたいです。
とりあえず、学習時に時刻tの出力を時刻t+1の入力にしたい問題は擬似的に解決できました。
ただ一点注意として、学習後の推論ではGround Truthが存在しないので、結局時刻tの出力を時刻t+1の入力とすることになります。
この時、学習時と推論時で与えられていた入力の質に差が生まれ、推論時にまともな出力が得られないことがあります。これをExposure Biasというようです。
上記のようなTeacher Forcingを含む基本的なSeq2Seqについては、Keras Blogの記事として紹介されています。
課題2 -Attentionを実装できるか
RNN Encoder-DecoderにおいてAttention機構が初めて提案されたのは、Bahdanau et.al(2015)です。
 図は[Bahdanau et.al(2015)](https://arxiv.org/abs/1409.0473)より抜粋
図は[Bahdanau et.al(2015)](https://arxiv.org/abs/1409.0473)より抜粋
図は、Encoder(Bi-directional LSTM)の各時刻の出力$h_i$を重み$α_t,_i$で足し合わせ、Decoderの LSTMに入力することを意味しています。これだけなら簡単かと思ったのですが、Decoder時刻tにおける$α_i$の算出には、時刻t-1のDecoder LSTMの出力が用いられるので、ここでも”時刻tの出力を時刻t+1で用いる”必要が出ました。
しかも、Ground Truthはありません。
Seq2Seqのライブラリを公開しているfarizrahman4uさんはこの構造でAttentionを実装したようですが、モデル構造を細かくいじって試してみたいな、という思いがあり、別の方法を模索し始めました。
Luong Global Attentionならいけるかも?
続けて読んだLuong et.al(2015)では、2つのAttentionが提唱されています。
Global Attention:
Bahdanau et.al(2015)と類似しているが、よりシンプルな構造
Local Attention:
Hard AttentionとSoft Attentionの混合
(Hard Attentionとは、どの時刻のEncoder出力に注目するか0か1で決めてしまうような手法で、Soft Attentionとは、全時刻のEncoder出力を重み付けして足し合わせる手法です。)
 図は[Luong et.al(2015)](https://arxiv.org/abs/1508.04025)より抜粋
図は[Luong et.al(2015)](https://arxiv.org/abs/1508.04025)より抜粋
上の図はGlobal Attentionの模式図です。
Bahdanau et.al(2015)との差異としてLuong et.al(2015)では、Decoder LSTMの時刻tの出力$h_t$と、Encoderの各時刻の出力$h_s$を用いて重み$a_t$を計算しています(図中白い四角形)。
その重みで$h_s$を足し合わせて文脈ベクトル$c_t$を生成し(図中上の青い四角形)、$h_t$と$c_t$を連結したものを用いてSoftmaxの計算を行います(図中右上の灰色四角形)。
この構造ならば、Decoderの時刻tにおける計算は、Encoder各時刻の出力$h_s$と、Decoder LSTMの時刻tの出力$h_t$で完結するので、Attentionの計算が時刻をまたぐことはありません。
これならばできるかな、と思いました。
実装
前置きが長くなりましたが、以下のように実装してみました。
from keras import backend as K
from keras.models import Sequential, Model
from keras.activations import softmax
from keras.layers.core import Dense, Activation, RepeatVector, Permute
from keras.layers import Input, Embedding, Multiply, Concatenate, Lambda
from keras.layers.recurrent import GRU
from keras.layers.wrappers import TimeDistributed
input_length = 10
output_length = 8
embedding_dim = 100
num_vocab = 10000
num_units = 512
# encoder
# convert word_index into embedded vector
# fig1
enc_in = Input(shape=(input_length,), dtype='int32', name='enc_input')
enc_embedding = Embedding(input_dim=num_vocab,
output_dim=embedding_dim,
input_length = input_length,
trainable = True,
name='enc_embedding')
enc_embedded = enc_embedding(enc_in)
encoded, state = GRU(units=num_units,
return_sequences=True,
return_state=True,
name='enc_GRU')(enc_embedded)
# \fig1
# decoder
# fig2
dec_in = Input(shape=(output_length,), dtype='int32', name='dec_input')
dec_embedding = Embedding(input_dim=num_vocab,
output_dim=embedding_dim,
input_length =output_length,
trainable = True,
name='dec_embedding')
# share weights with encoder embedding layer
dec_embedding.embeddings = enc_embedding.embeddings
dec_embedded = dec_embedding(dec_in)
decoded = GRU(units=num_units,
return_sequences=True,
name='dec_GRU')(dec_embedded, initial_state=state)
# Luong's global attention
repeat_dec = TimeDistributed(RepeatVector(input_length),
name='repeat_dec')
rep_decoded = repeat_dec(decoded)
# /fig2
# fig3
annotation_layer = TimeDistributed(Dense(units=num_units),
name='annotation_layer')
annotation = annotation_layer(encoded)
repeat_enc = TimeDistributed(RepeatVector(output_length),
name='repeat_enc')
rep_annotation = repeat_enc(annotation)
rep_annotation = Permute((2,1,3),
input_shape=(input_length, output_length, num_units),
name='permute_rep_annotation')(rep_annotation)
# fig4
attention_mul = Multiply(name='attention_mul')
elem_score = attention_mul([rep_decoded, rep_annotation])
score = Lambda(lambda x: K.sum(x, axis=3, keepdims = True), name='score')(elem_score)
attention_weight = Lambda(lambda x: softmax(x, axis=2),name='attention_weight')(score)
context_mul = Multiply(name='context_mul')
# \fig4
# fig5
rep_encoded = repeat_enc(encoded)
rep_encoded = Permute((2,1,3),
input_shape=(input_length, output_length, num_units),
name='permute_rep_encoded')(rep_encoded)
elem_context = context_mul([rep_encoded, attention_weight])
context = Lambda(lambda x: K.sum(x, axis=2), name='context')(elem_context)
concat = Concatenate(axis=-1)
dec_and_att = Lambda(lambda x: K.concatenate([x[0],x[1]], axis=-1), name='dec_att_concat')([decoded, context])
# \fig5
# full_connection and output
# fig6
fc1 = TimeDistributed(Dense(units=num_units*2), name='fc1')(dec_and_att)
fc1_activated = Activation('tanh')(fc1)
fc2 = TimeDistributed(Dense(units=num_vocab), name='fc2')(fc1_activated)
preds = Activation('softmax', name='softmax')(fc2)
# \fig6
model = Model([enc_in, dec_in], preds)
model.summary()
実装内容の説明
教師データについて:
ニューラル機械翻訳の分野などでは一般的ですが、文章中の単語を語彙のインデックス番号に置き換えた、各要素がint型であるようなシーケンスを入力としています。Encoder入力、Decoder入力ともに同じです。Decoder入力はTeacher Forcingなので、時刻が1つずれたものになります。
このあたりは、上述の[Keras Blogの記事](https://blog.keras.io/a-ten-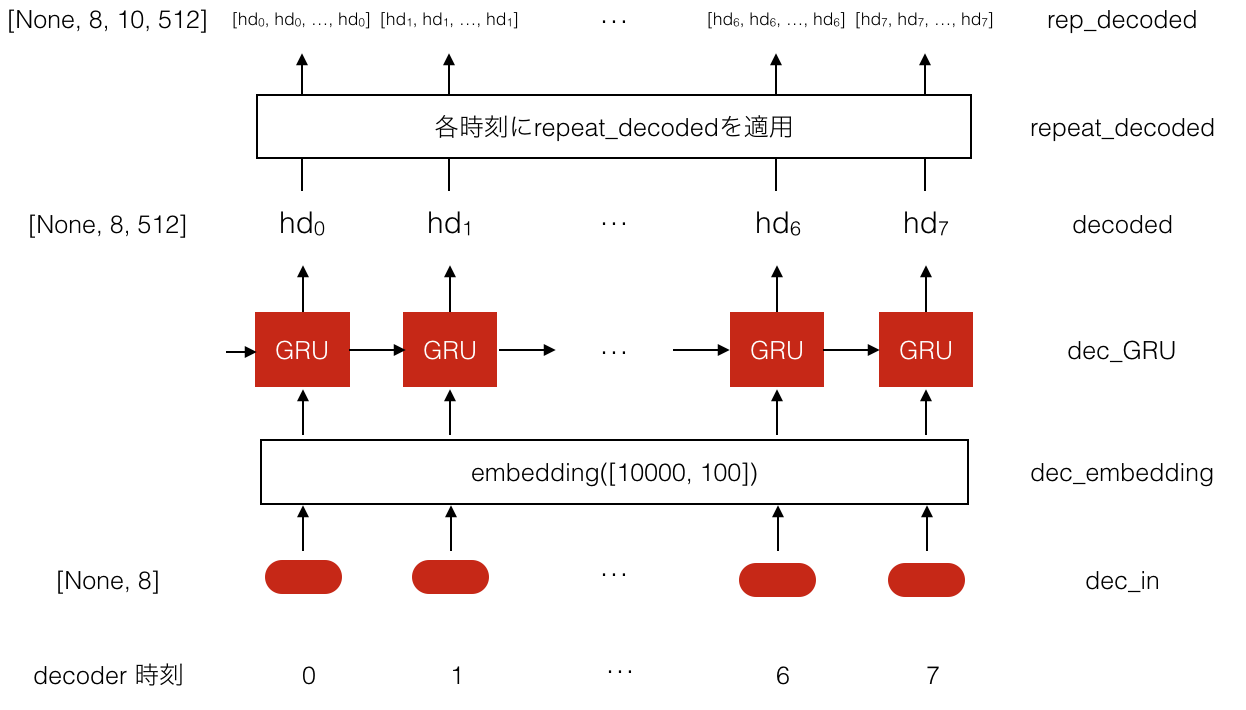
minute-introduction-to-sequence-to-sequence-learning-in-keras.html)を参考にしましたので、ご参照ください。
モデル構造の図示:
ソースコードに、対応するコードの範囲をfig, /figのように囲んであります。
また、図の右に変数名、またはレイヤーの名前を書いてあります。
図の左にデータの次元が書いてあり、0次元目のNoneはミニバッチ用の次元です。
ところどころスペルを指摘されて赤線が引かれていますが、気にしないでください。
煩雑になり苦しいですが、なるべく分かりやすく説明しようと思います。
根本的には、時間方向優先に計算されてしまうのならば、うまくデータを複製して一気に計算が行えるようにすれば良い、という考え方です。
ここは、特別なところはありません。入力されたインデックスのシーケンスを入力(enc_in)として受け取り、embedding layerを通して、ベクトル表現にします。
次に、GRUに順に入力して、各時刻のEncoder出力$he$を得ます。なお、Luong et.al(2015)ではLSTMが用いられていますが、今回はGRUを用いました。
この図の下半分も特別なことはありません。Teacher Forcingとして入力されたインデックスのシーケンスについて、embedding layerを通してベクトル表現にした後、GRUに順に入力して、各時刻のDecoder出力$hd$を得ます。
上半分がポイントです。
Timedistributed(RepeatVector())によって、各時刻のDecoder出力を、入力シーケンスの長さ分複製します。入力シーケンスの長さを10としたので、Decoder8回分の出力それぞれが、長さ10に複製されることになります。
fig3では、Encoder出力の処理に戻ります。ここもポイントです。
原論文のAttention計算方法のうち、generalに従います。各時刻のEncoder出力$he$を一度Denseレイヤーで線形変換し、$ha$とします。
次に、各時刻の$ha$を出力シーケンスの長さ分(ここでは長さ8)複製した後、テンソルの1次元目と2次元目を入れ替えます。図にあるように、各時刻の$ha$が一並びになったものが、出力シーケンスの長さ分だけできました。
fig4の下に、Encoder出力を線形変換し、複製し、次元を入れ替えたもの(rep_annotation)と、Decoder出力を複製したもの(rep_decoded)が並んでいます。次元は揃っています。
これらを要素ごとに掛け合わせ、要素ごとのスコア(elem_score)を算出します。
次に、3次元目の方向に要素ごとのスコアを足し合わせます。これにより、長さが8(出力シーケンス長)で、その各要素の長さが10(入力シーケンス長)であるベクトル(attention_weight)が生成されました。これが、Decoder各時刻における、Encoder出力の重み$a$になります。
fig5の下半分では、fig3と同じような処理がなされます。
各時刻のEncoder出力$he$を出力シーケンスの長さ分複製した後、テンソルの1次元目と2次元目を入れ替えます(rep_encoded)。
これと、fig4で算出した重み$a$を掛け合わせます。
できたベクトルを2次元目の方向に足し合わせることで、Decoderの各時刻についての文脈ベクトル$c$が算出されます。
fig6は特別なことはありません。
Dense(全結合層)によって出力語彙の次元に変換し、Softmaxで正規化します。
以上です。
誤りなどありましたら、ぜひご指摘いただきたく。
最後に(Githubの始め方指南求む)
コード管理ツールを使っていない、かなりプリミティブな開発スタイルなので、
Githubを使いたいのですが、腰が上がらず。
ケツを叩いてくれる背中を押してくれる方、募集中。






