最近、状態空間モデルを使用したDifference in Differenceの分析であるCausalImpactを見かける機会がちらほらあったので、とりあえずパッケージを使用してみようと思います。具体的にはWikipediaのページ「陰謀論」の閲覧数が2021年1月6日の連邦議会議事堂襲撃事件によって増加したかどうか見ていきます。
Wikipedia「陰謀論」のページ
ウィキペディアのページ閲覧数は、Rの場合pageviewsパッケージ によって取得可能です。まず、article_pageviews()によってページの閲覧数を収集します。
library(tidyverse)
library(pageviews)
library(WikipediR)
library(CausalImpact)
conspiracy_trend <- article_pageviews(project = "ja.wikipedia",
article = "陰謀論",
start = "2020010100", #取り込み開始時期
end = "2021053100") #取り込み終了時期
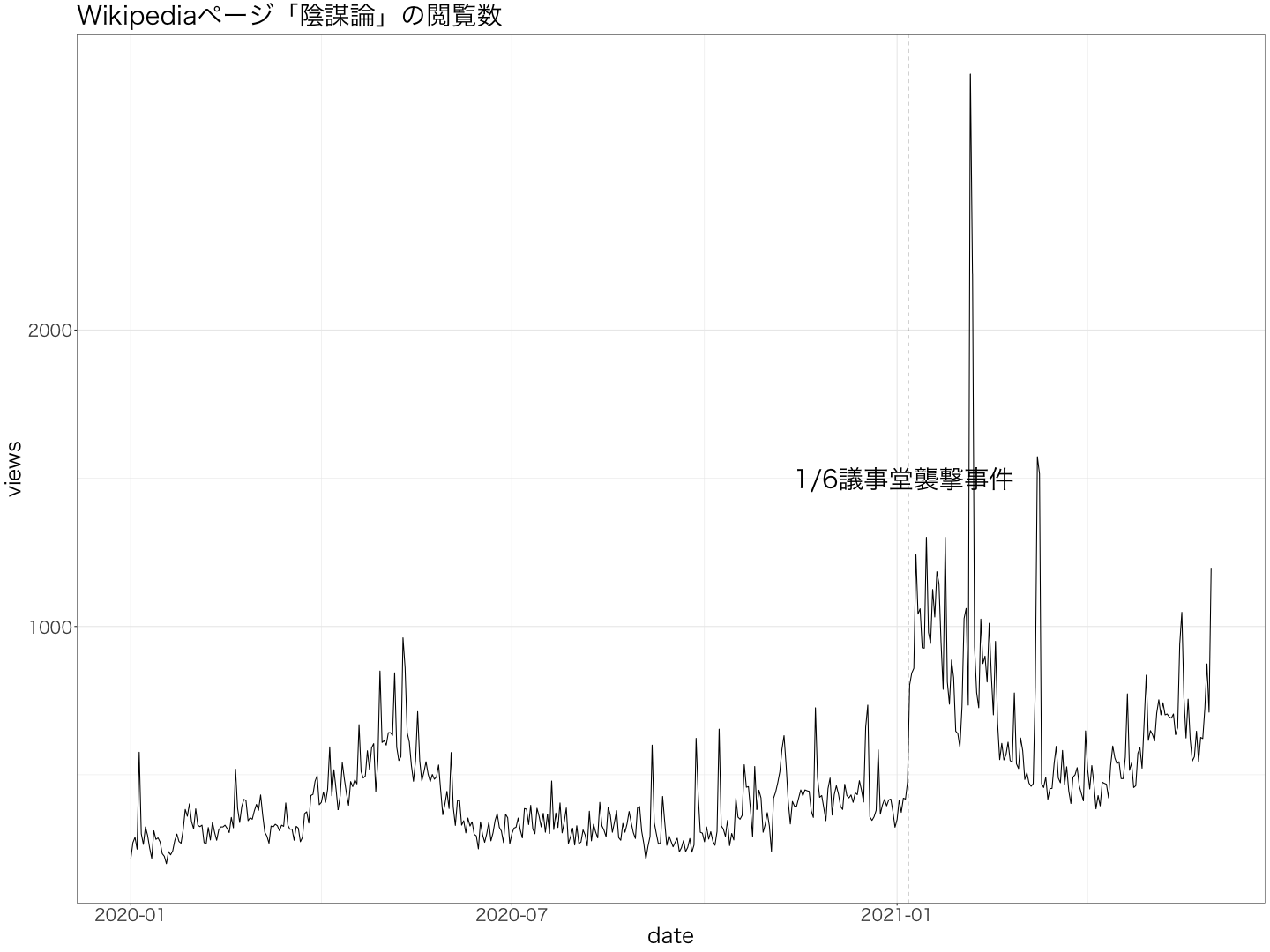
とりあえず閲覧数の動向を図示してみます。
conspiracy_trend %>%
ggplot() +
geom_line(aes(x = date, y = views)) + #viewsは閲覧数
geom_vline(xintercept = as.POSIXct("2021-01-06 15:00:00"), linetype = "dashed") +
annotate("text",x = as.POSIXct("2021-01-04 15:00:00"), y = 1500,
label = "1/6議事堂襲撃事件",family = "HiraKakuProN-W3" ) +
theme_bw(base_family = "HiraKakuProN-W3") +
labs(title = "Wikipediaページ「陰謀論」の閲覧数") +
theme(legend.position = "none")
図はこんな感じです。やや見えにくいですが、1/6の議事堂襲撃事件後に閲覧数が増えていることが見て取れます。
CausalImpact
実際に1/6の議事堂襲撃事件が閲覧数を増加させたのか、CausalImpactを使用して見ていこうと思います。CausalImpactについてはこちらを参考にして見て見ました。
まず、CausalImpactをするためのデータを作成します。
# 分析データ作成
data_wiki <- conspiracy_trend %>%
dplyr::select(date, views) %>%
mutate(date = as.Date(date))
次に、どの期間を訓練データにし、どの期間をテストデータにするか決めます。今回はとりあえず2020/7/1~ 2021/1/6までを訓練データ期間、2021/1/7~2021/1/31をテストデータ期間としています。
pre.period <- as.Date(c("2020-07-01", "2021-01-06"))
post.period <- as.Date(c("2021-01-07", "2021-01-31"))
最後にCausalImpactの分析を行います。
impact <- CausalImpact(data_wiki, pre.period, post.period)
plot(impact)
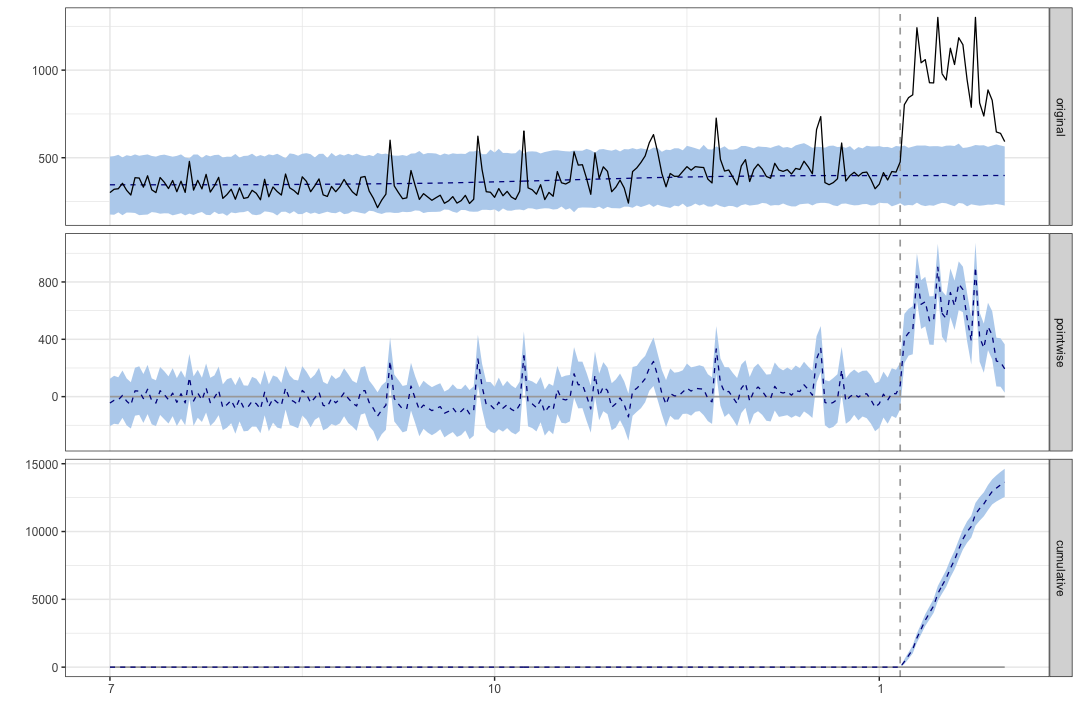
結果はこうなっています。一番上の図は実測値(実線)と予測値(点線)の比較です。(青いエリアは95%CI)1/6時点までのデータを学習して生み出された予測と比較すると、1/7以後の閲覧数はかなり上振れしていることがわかります。
2番目の図は実測値と予測値の差を表しています。
3番目の図は実測値と予測値の差の累積です。
具体的にどの程度閲覧数を増加させたのか見てみます。
summary(impact)
Average Cumulative
Actual 944 23593
Prediction (s.d.) 398 (21) 9959 (525)
95% CI [359, 441] [8964, 11037]
Absolute effect (s.d.) 545 (21) 13634 (525)
95% CI [502, 585] [12556, 14629]
Relative effect (s.d.) 137% (5.3%) 137% (5.3%)
95% CI [126%, 147%] [126%, 147%]
Posterior tail-area probability p: 0.00105
Posterior prob. of a causal effect: 99.89496%
For more details, type: summary(impact, "report")
Averageは1/7~1/31までの平均値、Cumulativeは1/7~1/31までの合計(累積)値を意味しています。最初の段落では実測値(Actual)、予測値(Prediction)が記載されています。次の段落では実測値と予測値の差が記載されています。最後の段落では予測値とし比較した実測値の増加割合を意味しています。
平均して1日あたり546回閲覧数を増加させていることがわかります。また、1月末までの間で計1364回閲覧数を増加させたことがわかります。
この分析は適当にやっていますが、実際なんらかの分析をする際には共変量などを含めて計算したり時系列モデルを修正したりしないといけないと思われます。