C#で特殊ElGamal暗号アルゴリズムを実装してみた

はじめに

今回、ElGamal暗号について学習も兼ねて、C#でアルゴリズムを実装してみました．

作るにあたり、以下を参考にさせて頂きました．

IPUSIRON様
- 暗号技術のすべて

stackoverflow様
- Calculate square root of a BigInteger (System.Numerics.BigInteger)

Wikipedia様
-ElGamal暗号

ElGamal暗号とは

ElGamal暗号とは、1984年にエルガマルによって提案された暗号です．
- 暗号文は平文の約2倍の大きさ
- 暗号化の際に乱数でマスクをする
- 暗号の一方向性は CDH問題 の困難性と等価

暗号の詳しい内容は省略

実装

環境

• Windows 10
• Visual Studio 2019 Community
• C#
• .NET Framework 4.7.2

基本

ElGamalクラスを作成します

using System;
using System.Numerics;

class ElGamal
{
    // セキュリティパラメータ（バイト数）
    public int K { get; private set; }

    // デバッグ以外ならprivateに設定
    public BigInteger p;
    public BigInteger g;
    public BigInteger y;
    public BigInteger x;

    // 公開鍵
    public (BigInteger p, BigInteger g, BigInteger y) Pk
    {
        get => (this.p, this.g, this.y);
        set
        {
            this.p = value.p;
            this.g = value.g;
            this.y = value.y;
        }
    }
    // 秘密鍵
    // デバッグ以外ならprivateに設定
    public BigInteger Sk
    {
        get => this.x;
        set => this.x = value;
    }

    private Random random;
}

また、

min<=x<=maxのmaxByteの正整数を生成する

private BigInteger GenerateRandom(int maxByte, BigInteger min, BigInteger max)

と、
maxByteの奇数の素数を生成する

private BigInteger GenerateRandomPrime(int maxByte)

があります．

鍵の生成

素数p、原始元g、ランダムな整数x、整数yを作ります

また原始元gは、満たす原始元を2から1ずつ探しています

// 鍵を生成する
public void GenerateKeys(int k)
{
    p = GenerateRandomPrime(k);
    Console.WriteLine("ランダムな素数p = {0}", p);

    g = GenerateGroupGen(k, p);
    Console.WriteLine("原始元g = {0}", g);

    x = GenerateRandom(k, 0, p - 2);
    Console.WriteLine("ランダムな非負整数x = {0}", x);

    y = BigInteger.ModPow(g, x, p);
    Console.WriteLine("y = g^x mod p = {0}", y);
}

// 原始元を生成する
public static int GenerateGroupGen(int k, BigInteger p)
{
    for (int g = 2; ; g++)
    {
        bool isGen = true;
        BigInteger a = 1;
        for (int i = 1; i <= p - 2; i++)
        {
            a *= g;
            if (a >= p) a %= p;
            if (a == 1)
            {
                isGen = false;
                break;
            }
        }

        if (isGen)
        {
            return g;
        }
    }
}

暗号化

平文mから暗号文cを生成します

// 暗号化する
public (BigInteger c1, BigInteger c2) Encrypt(BigInteger m)
{
    var r = GenerateRandom(K, 0, p - 2);
    Console.WriteLine("ランダムな数r = {0}", r);

    var c1 = BigInteger.ModPow(g, r, p);
    var c2 = (m * BigInteger.ModPow(y, r, p)) % p;

    return (c1, c2);
}

復号

暗号文cから平文m'を生成します

// 復号する
public BigInteger Decrypt((BigInteger c1, BigInteger c2) c)
{
    return (c.c2 * BigInteger.ModPow(c.c1, p - 1 - x, p)) % p;
}

結果

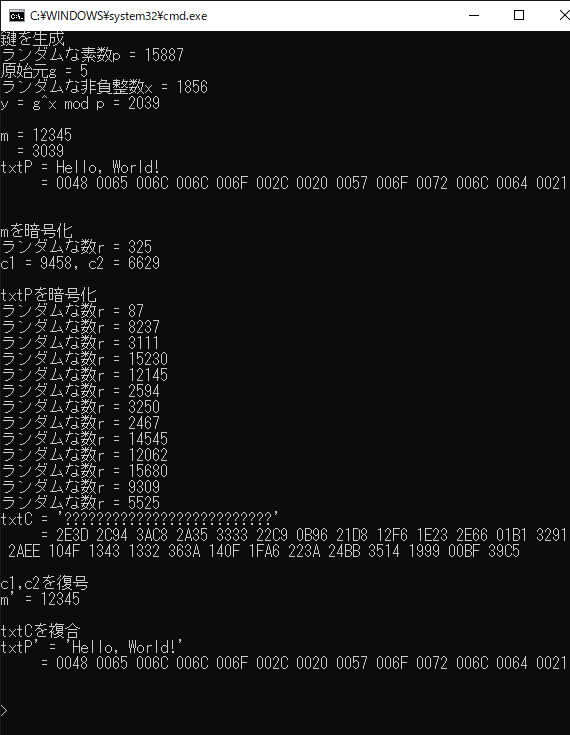
実際に任意の数字m（今回は12345）と任意の文字列（今回は"Hello, World!"）を暗号化・復号してみます．
なお、文字列ですが、UTF-16として用い、ECBモードで行います．

以上の画像のように無事に暗号化・復号できました．

最後に

実際に実装してみました．
素数 p ですが、本来ならば p-1 が大きな素因数を含むのが望ましいのですが、今回はランダムな素数にしました．次は p-1 が含むような素数を作りたいです．
また今回は位相が素数である巡回群でしたが、次はあらゆる巡回群を扱えるようにもしたいです．

ソースコード

当記事に間違い等ありましたら、お手数ですがコメント欄よりご指摘頂けますと幸いです。