表題の通り、変数を対数化した場合のモデルの解釈についてはさまざまに良い記事があるのですが、人に説明するときに以下のポイントを考えて説明するので、整理してみました。
- どんなデータの時に対数化がよく当てはまるのか?
- %近似する解説が多いので、近似しない解説
以下記事のまとめ方が美しかったので参考にさせていただきました。
まとめ
データの傾向
| x | log(x)すると良い | |
|---|---|---|
| y | 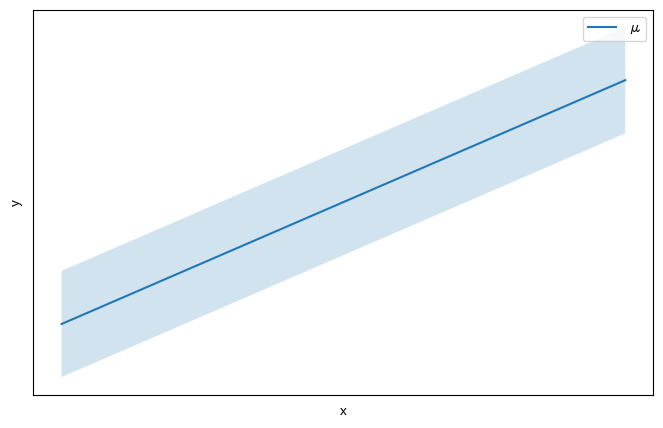 |
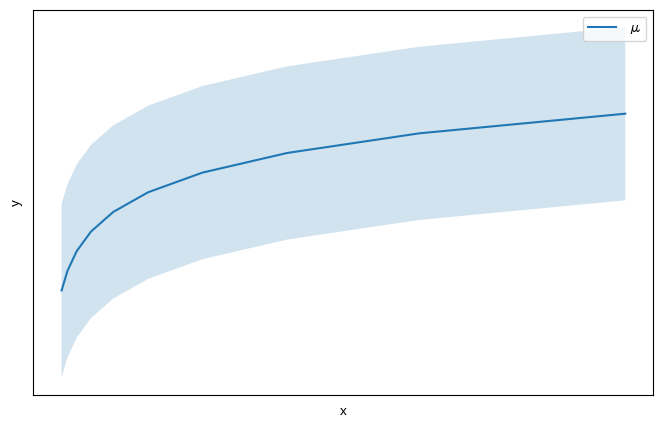 |
| log(y)すると良い | 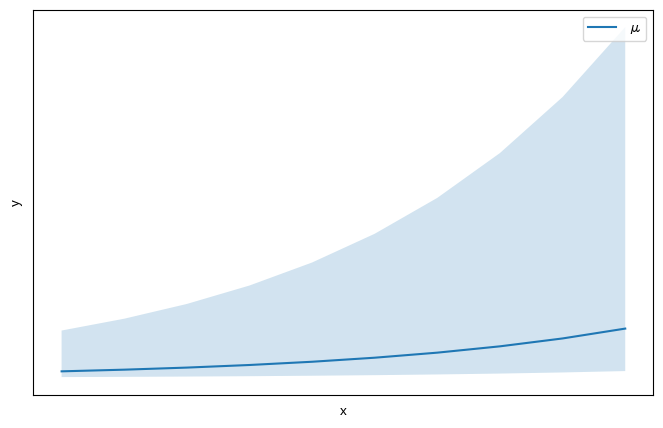 |
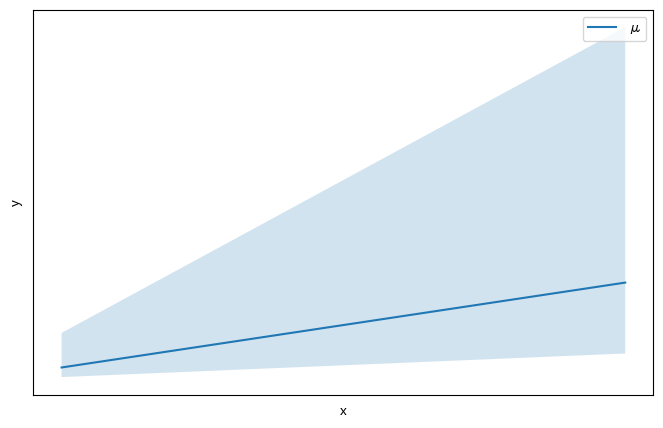 |
解釈
| x | log(x) | |
|---|---|---|
| y | xが1増加するとyがβ増加 | nを任意の値でxをn倍するとyがβlog(n)増加 |
| log(y) | xが1増加するとyがexp(β)倍 | nを任意の値でxをn倍するとyがn^β倍 |
log(x)とする場合
$x$ だけを対数化して $y = \alpha + \beta\log(x)$ と仮定する場合です。
データの傾向
以下のようなデータの傾向の場合は $x$ を対数化するとよく当てはまります。
以降の図で共通ですが, 変数変換すると $y$ は $\mu$ を中心とした等分散の正規分布を仮定したことになります。

回帰係数の解釈
$y = \alpha + \beta\log(x)$なので、
$y_0 = \alpha + \beta\log(x)$,
$y_1 = \alpha + \beta\log(x\times n)$, $n$は任意の値として
$y_1-y_0$を解いていきます。
\begin{align}
y_1-y_0 &= \alpha + \beta\log(x\times n) -(\alpha + \beta\log(x)) \\
&= \beta\log(x\times n) - \beta\log(x)\\
&= \beta\log\left(\frac{x\times n}{x}\right)\\
&= \beta\log(n)
\end{align}
よって、$x$ を $n$ 倍すると $y$ が $\beta\log(n)$ 増加する。と解釈できます。
例えば、$\beta=5, n=2$の場合は, $log(n)\risingdotseq 0.693$なので、
$x$ を2倍すると $y$ が $5×0.693\risingdotseq3.466$増加する。と解釈できます。
log(y)とする場合
$y$ だけを対数化して $ \log(y) = \alpha + \beta x$ と仮定する場合です。
データの傾向
以下のようなデータの傾向の場合は $y$ を対数化するとよく当てはまります。

回帰係数の解釈
$\log(y) = \alpha + \beta x$なので、
$\log(y_0) = \alpha + \beta x$,
$\log(y_1) = \alpha + \beta (x+1)$として
$\log(y_1)-\log(y_0)$ を解いていきます。
\begin{align}
\log(y_1)-\log(y_0) &= \alpha + \beta (x+1) - (\alpha + \beta x) \\
\log(y_1)-\log(y_0) &= \beta\\
\log\left(\frac{y_1}{y_0}\right) &=\beta,\\
\frac{y_1}{y_0} &= exp(\beta)
\end{align}
つまり、$x$ が1増加すると、$y$ が $exp(\beta)$ 倍になる。と解釈できます。
log(x), log(y)とする場合
どちらも対数化して $ \log(y) = \alpha + \beta \log(x)$ と仮定する場合です。
データの傾向
以下のようなデータの傾向の場合は $x, y$ を対数化するとよく当てはまります。

回帰係数の解釈
$\log(y) = \alpha + \beta\log(x)$なので、
$\log(y_0) = \alpha + \beta\log(x)$,
$\log(y_1) = \alpha + \beta\log(x\times n)$, $n$は任意の値として
$\log(y_1)-\log(y_0)$を解いていきます。
\begin{align}
\log(y_1)-\log(y_0)&= \alpha + \beta\log(x\times n) -(\alpha + \beta\log(x)) \\
&= \beta\log(x\times n) - \beta\log(x)\\
&= \beta\log\left(\frac{x\times n}{x}\right)\\
&= \beta\log(n)\\
&= \log(n^\beta)\\
\log\left(\frac{y_1}{y_0}\right)&= \log(n^\beta)\\
\frac{y_1}{y_0}&= n^\beta
\end{align}
よって、$x$ を $n$ 倍すると $y$ が $n^\beta$倍になる。と解釈できます。
以上