LoginSignup
1
1

More than 5 years have passed since last update.

@HiroshiATakano(Hiroshi Takano)

Pystanで単回帰分析

Posted at

「StanとRでベイズ統計モデリング」 Chapter7より

交互作用

回帰分析において説明変数同士の掛け算の項を考慮すること

対数をとるか否か

モデル式７－１

$ \mu[n]= b_1+b_2Area[n] $
$ Y[n] \sim Normal(\mu[n],\sigma_Y) $

関東近郊の架空の賃貸物件データ

d = pd.read_csv("input/data-rental.txt")
sns.set_style("whitegrid")
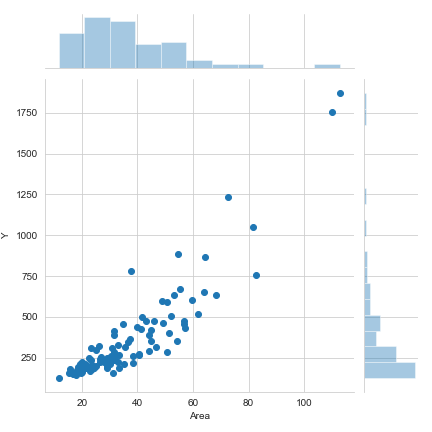
sns.jointplot(x="Area",y="Y",data=d)

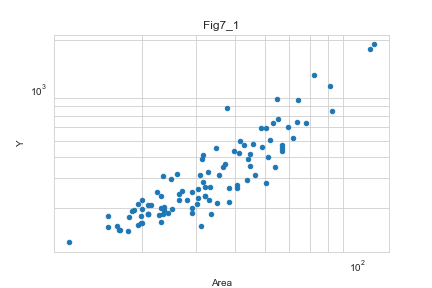
d.plot.scatter(x='Area',y='Y')
plt.yscale('log')
plt.xscale('log')
plt.grid(which="both")

plt.xlabel("Area")
plt.ylabel("Y")
sns.set_style('whitegrid')
plt.title('Fig7_1')

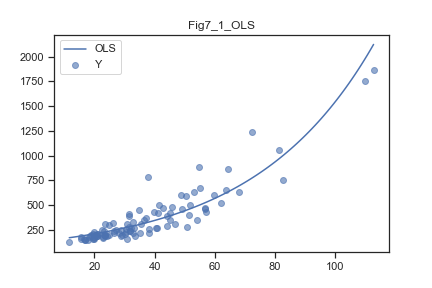
散布図：
横軸に説明変数、縦軸に応答変数
fig_7_1_left.png
両対数軸でプロット
fig_7_1_right.png

mdl = glm("Y~Area",data=d,family=sm.families.Poisson()).fit()

plt.scatter(d['Area'], d['Y'], alpha=0.6)
xx = np.linspace(min(d['Area']),max(d['Area']),100)
plt.plot(xx, np.exp(mdl.params[0]+mdl.params[1]*xx), 'b-', label='OLS')
plt.legend()
plt.title('Fig7_1_OLS')

fig_7_1_OLS.png

stanmodel = StanModel(file="model/model7-1.stan")
Area_new = np.linspace(10,120,50)
data_ = {'N':len(d),'Area':d['Area'],'Y':d['Y'],'N_new':50,'Area_new':Area_new}
fit1 = stanmodel.sampling(data=data_,n_jobs=-1,seed=1234)
ms1 = fit1.extract()

col = np.linspace(10,120,50)
df2 = pd.DataFrame(fit1['y_new'])
df2.columns = col


qua = [0.1, 0.25, 0.50, 0.75, 0.9]
d_est = pd.DataFrame()

for i in np.arange(len(df2.columns)):
    for qu in qua:
        d_est[qu] = df2.quantile(qu)

x = d_est.index
y1 = d_est[0.1].values
y2 = d_est[0.25].values
y3 = d_est[0.5].values
y4 = d_est[0.75].values
y5 = d_est[0.9].values


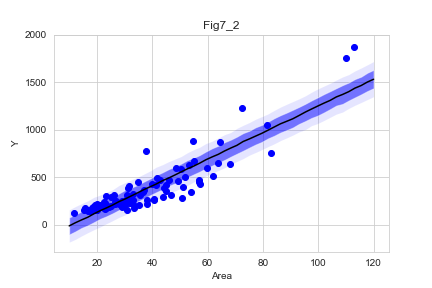
plt.fill_between(x,y1,y5,facecolor='blue',alpha=0.1)
plt.fill_between(x,y2,y4,facecolor='blue',alpha=0.5)
plt.plot(x,y3,'k-')
plt.scatter(d["Area"],d["Y"],c='b')
plt.xlabel("Area")
plt.ylabel("Y")
sns.set_style('whitegrid')
plt.title('Fig7_2')

予測分布：
80%ベイズ予測区間が負の値を含む
fig_7_2_left.png

d_ori = d

quantile = [10,50,90]
colname = ['p'+str(x) for x in quantile]
d_qua = pd.DataFrame(np.percentile(ms1["y_pred"],q=quantile,axis=0).T,columns=colname)
d_ = pd.concat([d_ori,d_qua],axis=1)
d0 = d_


palette = sns.color_palette()
fig = plt.figure(figsize=(10,8))

ax = fig.add_subplot(1,1,1)
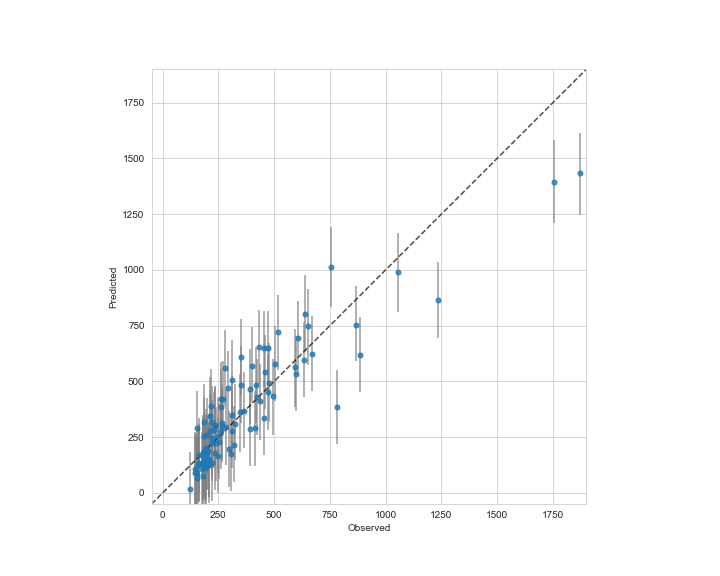
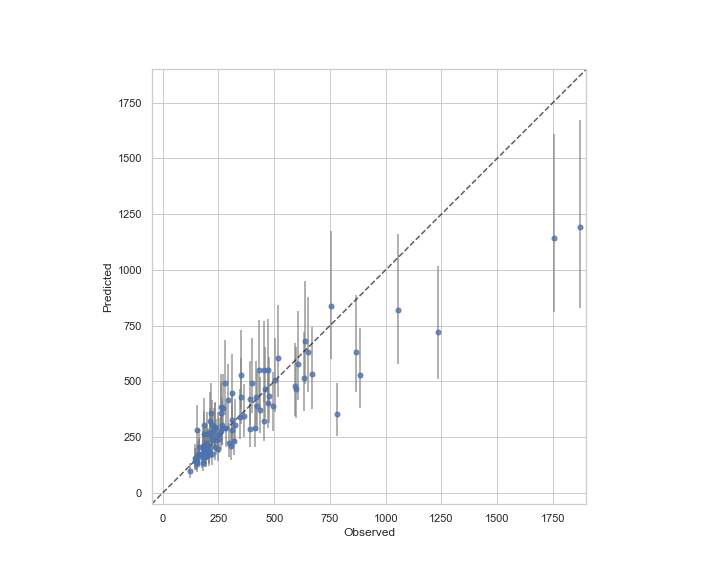
ax.plot([-50,1900],[-50,1900],'k--',alpha=0.7)
ax.errorbar(d0.Y,d0.p50,yerr=[d0.p50-d0.p10,d0.p90-d0.p50],
                             fmt='o',ecolor='gray',ms=5,mfc=palette[0],alpha=0.8,marker='o')

ax.set_aspect('equal')
ax.set_xlim(-50,1900)
ax.set_ylim(-50,1900)
ax.set_xlabel("Observed")
ax.set_ylabel("Predicted")

実測値と予測値のプロット

fig_7_3_left.png

N_mcmc = len(ms1['lp__'])
d_noise = pd.DataFrame(-ms1['mu']+np.array(d_ori['Y']))
col = d_noise.columns
d_noise.columns = ["noise" + str(col[i]+1) for i in np.arange(len(col))] 

data = d.copy()
data = data.sort_values(by="Area")

d_est = pd.concat([pd.DataFrame({"mcmc":np.arange(1,N_mcmc+1)}),d_noise],axis=1)

col = d_est.columns
est = []

fig = plt.figure(figsize=(10,8))
sns.set_style('whitegrid')
sns.set(font_scale=1)


for i in np.arange(1,len(d_est.columns)):
    data = d_est[col[i]]
    density = gaussian_kde(data)
    xs = np.linspace(min(data),max(data),100)
    plt.plot(xs,density(xs),'k-',lw=0.5)
    xx = xs[np.argmax(density(xs))]
    plt.vlines(xx,0,max(density(xs)),colors='k',linestyle="-.",alpha=0.5,linewidth=0.5)

    est.append(xs[np.argmax(density(xs))])

plt.xlabel("Value")
plt.ylabel("density")

s_dens = gaussian_kde(ms1['s_Y'])

xs = np.linspace(min(ms1['s_Y']),max(ms1['s_Y']),100)
s_MPA = xs[np.argmax(s_dens(xs))]
print(s_MPA)
rv = norm(loc=0,scale=s_MPA)

bw = 25
bins = np.arange(min(est),max(est),bw)

fig = plt.figure(figsize=(10,8))
sns.set_style('whitegrid')
sns.set(font_scale=1)

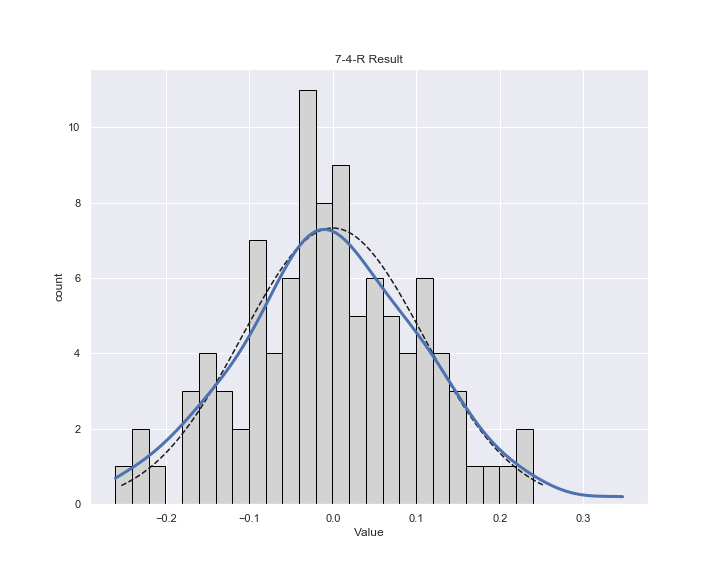
res = plt.hist(est,bins=bins,color='lightgray',edgecolor='black')
x = np.linspace(rv.ppf(0.01),rv.ppf(0.99), 100)

plt.plot(x,rv.pdf(x)*len(d)*bw,'k--')

data = est
density = gaussian_kde(data)
print(max(data))
xs = np.linspace(min(data),max(data),100)
plt.plot(xs,density(xs)*len(d)*bw,lw=3)

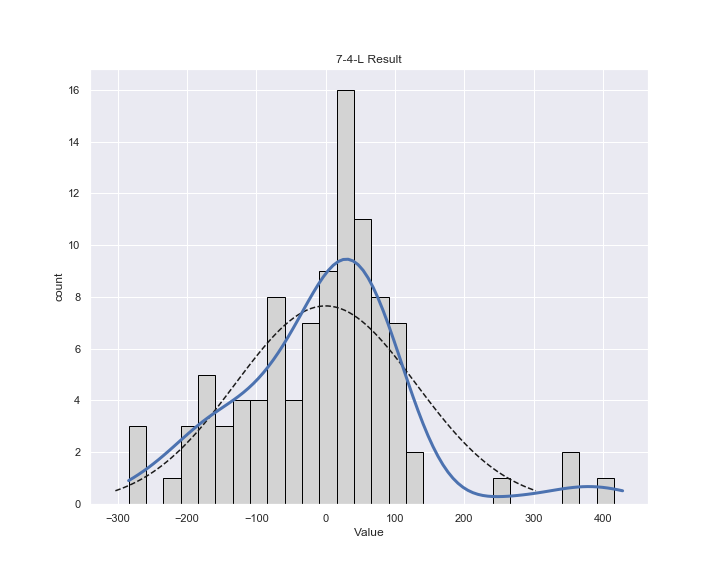
plt.title("7-4-L Result")
plt.xlabel("Value")
plt.ylabel("count")

測定されたノイズの分布
広くて費用が高い物件（Areaがおよそ70m2以上の物件）に結果がひきずられてノイズの分布が歪んでいて、正規分布との乖離がある
fig_7-4-L.png

モデル式７－２

YおよびAreaの対数をとって単回帰に使う
$ \mu[n]= b_1+b_2 log10(Area[n]) $
$ log10(Y[n]) \sim Normal(\mu[n],\sigma_Y) $

Area_new = np.linspace(10,120,50)
data_ = {'N':len(d),'Area':np.log10(d['Area']),'Y':np.log10(d['Y']),'N_new':50,'Area_new':np.log10(Area_new)}
fit2 = stanmodel.sampling(data=data_,n_jobs=-1,seed=1234)
ms2 = fit2.extract()

col = np.linspace(10,120,50)
df2 = pd.DataFrame(10**fit2['y_new'])
df2.columns = col


qua = [0.1, 0.25, 0.50, 0.75, 0.9]
d_est = pd.DataFrame()

for i in np.arange(len(df2.columns)):
    for qu in qua:
        d_est[qu] = df2.quantile(qu)

x = d_est.index
y1 = d_est[0.1].values
y2 = d_est[0.25].values
y3 = d_est[0.5].values
y4 = d_est[0.75].values
y5 = d_est[0.9].values


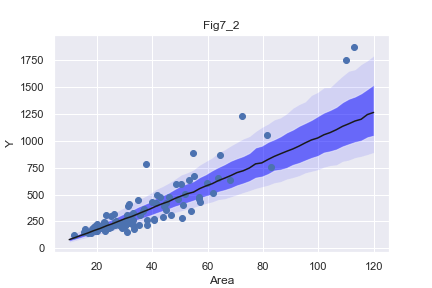
plt.fill_between(x,y1,y5,facecolor='blue',alpha=0.1)
plt.fill_between(x,y2,y4,facecolor='blue',alpha=0.5)
plt.plot(x,y3,'k-')
plt.scatter(d["Area"],d["Y"],c='b')

plt.xlabel("Area")
plt.ylabel("Y")
sns.set_style('whitegrid')
plt.title('Fig7_2')

fig_7_2_right.png


d_ori = d

quantile = [10,50,90]
colname = ['p'+str(x) for x in quantile]
d_qua = pd.DataFrame(np.percentile(10**ms2["y_pred"],q=quantile,axis=0).T,columns=colname)
d_ = pd.concat([d_ori,d_qua],axis=1)
d0 = d_


palette = sns.color_palette()
fig = plt.figure(figsize=(10,8))

ax = fig.add_subplot(1,1,1)
ax.plot([-50,1900],[-50,1900],'k--',alpha=0.7)
ax.errorbar(d0.Y,d0.p50,yerr=[d0.p50-d0.p10,d0.p90-d0.p50],
                             fmt='o',ecolor='gray',ms=5,mfc=palette[0],alpha=0.8,marker='o')

ax.set_aspect('equal')
ax.set_xlim(-50,1900)
ax.set_ylim(-50,1900)
ax.set_xlabel("Observed")
ax.set_ylabel("Predicted")

Areaが1000m2より大きい物件のベイズ予測区間は広くなっている

fig_7_3_right.png


N_mcmc = len(ms2['lp__'])
d_noise = pd.DataFrame(-ms2['mu']+np.array(np.log10(d_ori['Y'])))
col = d_noise.columns
d_noise.columns = ["noise" + str(col[i]+1) for i in np.arange(len(col))] 

data = d.copy()
data = data.sort_values(by="Area")

d_est = pd.concat([pd.DataFrame({"mcmc":np.arange(1,N_mcmc+1)}),d_noise],axis=1)

col = d_est.columns
est = []

fig = plt.figure(figsize=(10,8))
sns.set_style('whitegrid')
sns.set(font_scale=1)


for i in np.arange(1,len(d_est.columns)):
    data = d_est[col[i]]
    density = gaussian_kde(data)
    xs = np.linspace(min(data),max(data),100)
    plt.plot(xs,density(xs),'k-',lw=0.5)
    xx = xs[np.argmax(density(xs))]
    plt.vlines(xx,0,max(density(xs)),colors='k',linestyle="-.",alpha=0.5,linewidth=0.5)

    est.append(xs[np.argmax(density(xs))])

plt.xlabel("Value")
plt.ylabel("density")

s_dens = gaussian_kde(ms2['s_Y'])

xs = np.linspace(min(ms2['s_Y']),max(ms2['s_Y']),100)
s_MPA = xs[np.argmax(s_dens(xs))]
print(s_MPA)
rv = norm(loc=0,scale=s_MPA)

bw = 0.02
bins = np.arange(min(est),max(est),bw)

fig = plt.figure(figsize=(10,8))
sns.set_style('whitegrid')
sns.set(font_scale=1)

res = plt.hist(est,bins=bins,color='lightgray',edgecolor='black')
x = np.linspace(rv.ppf(0.01),rv.ppf(0.99), 100)

plt.plot(x,rv.pdf(x)*len(d)*bw,'k--')

data = est
density = gaussian_kde(data)
print(max(data))
xs = np.linspace(min(data),max(data),100)
plt.plot(xs,density(xs)*len(d)*bw,lw=3)

plt.title("7-4-R Result")
plt.xlabel("Value")
plt.ylabel("count")

fig_7-4-R.png

1
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
1