Abstract
円形物体を撮影すると、画像上では楕円となって、その形状から物体の3次元位置を解析することができます。そのため、画像から抽出した点群に対して楕円を当てはめることは、カメラのキャリブレーションやロボットの制御などに使われています。こちらの本をもとに、楕円当てはめを実装してみたので、その時のコードや結果を共有します。
Elliptic Formula
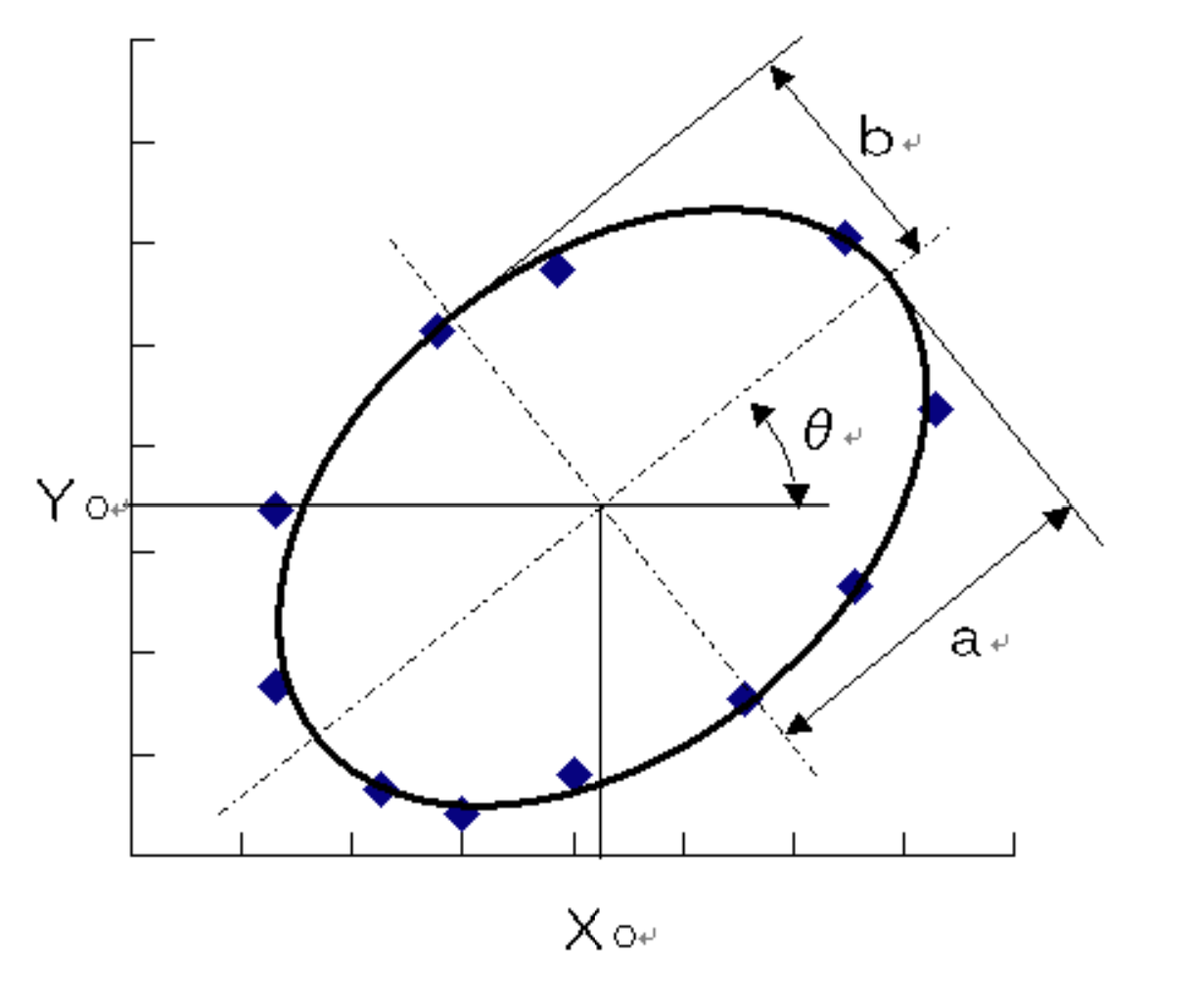
まず、楕円の式を共有します。楕円の中心を(Xc,Yc)、X軸の長さをa、Y軸の長さをb、楕円の傾きをθとすると以下の様になります。
\frac{((X-X_c)cos\theta+(Y-Y_c)sin\theta)^2}{a^2}+\frac{(-(X-X_c)sin\theta+(Y-Y_c)cos\theta)^2}{b^2}=1
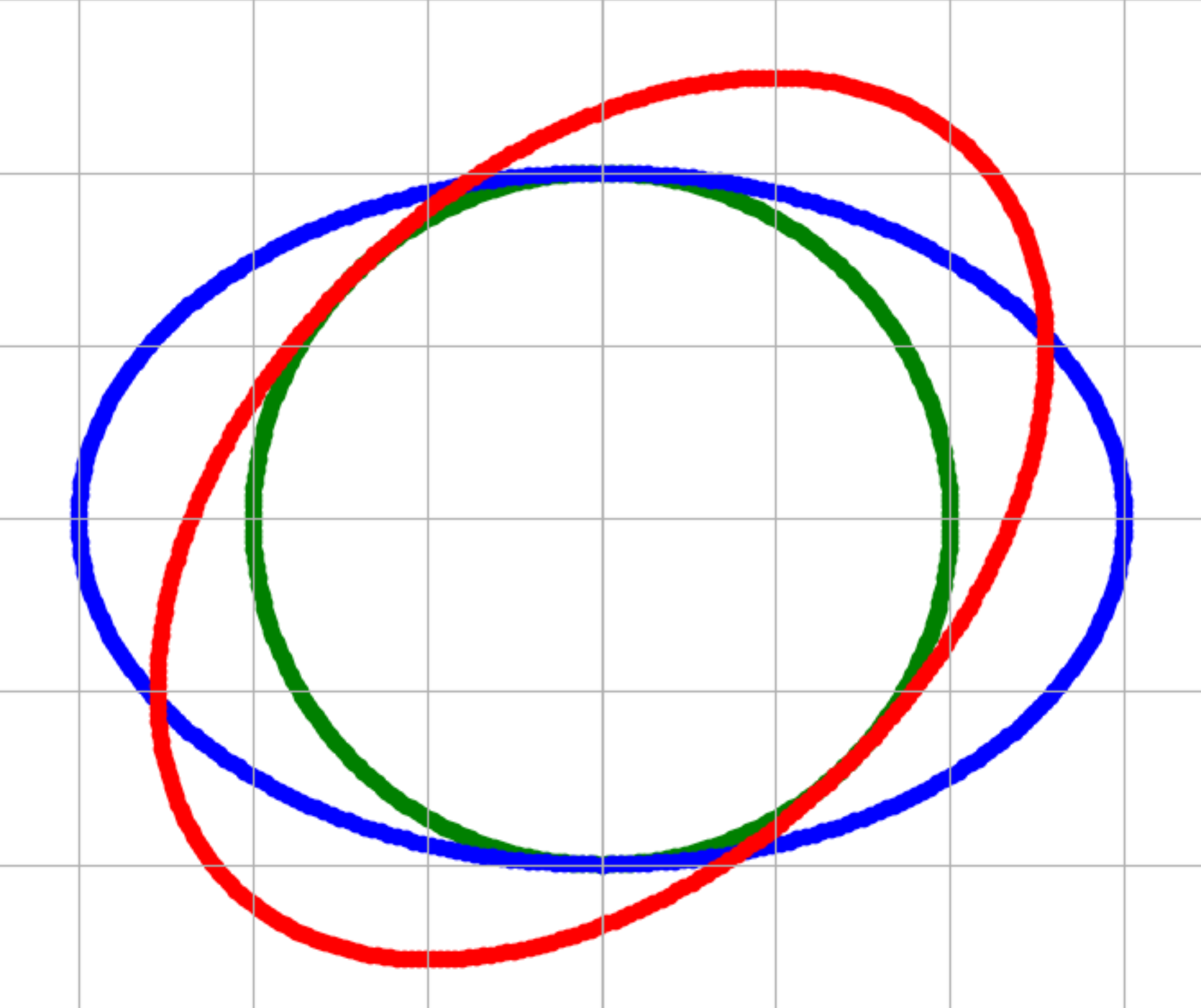
円や楕円に慣れるために楕円の式を描いてみましょう。こちらにpythonで実装したコードがあります。
Ellipse representation
画像上の楕円は、以下の式のように書くことができます。
Ax^2+2Bxy+Cy^2+2f_0(Dx+Ey)+f_0^2F=0...(1)
f0はスケールを調整する定数です。次の6次元ベクトルを定義し、
\xi=\begin{pmatrix}
x^2 \\
2xy \\
y^2 \\
2f_0x \\
2f_0y \\
f_0^2 \\
\end{pmatrix},
\theta=\begin{pmatrix}
A \\
B \\
C \\
D \\
E \\
F \\
\end{pmatrix}...(2)
ベクトルaとbの内積を(a, b)とすると、式(1)は次のように書けます。
(\xi,\theta)=0...(3)
楕円を当てはめることは、θを解くことと同義なので、その方法をまとめていきます。
Solution1: Least squares method
式(1)の形の楕円を、誤差をもつ点群(x_1,y_1),...,(x_N,y_N)(x1,y1),...,(xN,yN)に当てはめるには、次の式のA,B,C,D,E,Fを計算することになります。
Ax_\alpha^2+2Bx_\alpha y_\alpha+Cy_\alpha^2+2f_0(Dx_\alpha+Ey_\alpha)+f_0^2F\approx0, \alpha=1,..,N...(4)
式(3)を用いると、式(4)は次のように書けます。
(\xi_\alpha,\theta)\approx0, \alpha=1,..,N...(5)
最小二乗法を用いてθを計算する手順を紹介します。
1. 次の6x6行列Mを計算する
M=\frac{1}{N}\sum_{\alpha=1}^N\xi_\alpha\xi_\alpha^\intercal...(6)
2. 固有値問題を解き、最小固有値λに対する単位固有ベクトルθを求める
M\theta=\lambda\theta...(7)
これは条件∣θ∣=1 のもとで以下の2乗和を最小化します。
J=\frac{1}{N}\sum_{\alpha=1}^N(\xi_\alpha,\theta)^2=\frac{1}{N}\sum_{\alpha=1}^N\theta^\intercal\xi_\alpha\xi_\alpha^\intercal\theta=(\theta,M\theta)...(8)
これを最小化する単位ベクトルθは、行列Mの最小固有値の単位ベクトルです。一連の処理をPythonで実装したコードはこちらです。
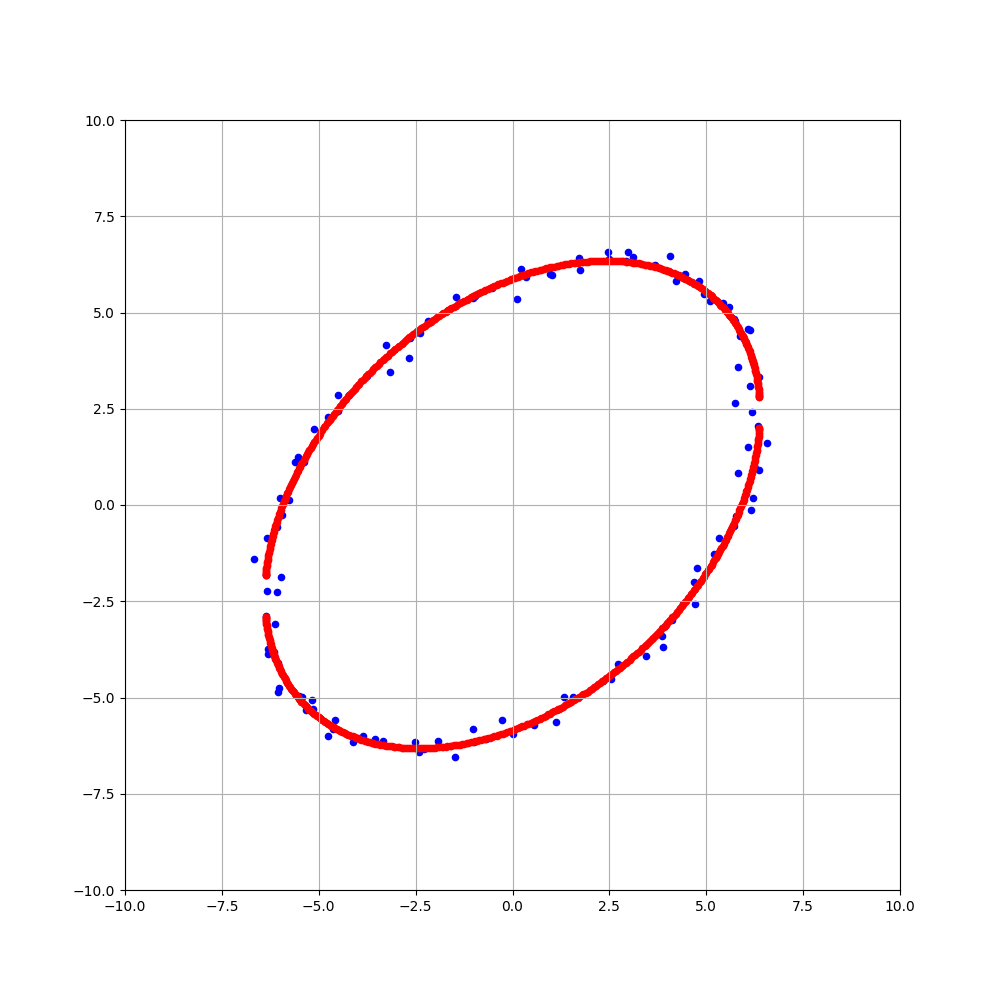
誤差を含んだ青点からθが計算されて、下の画像のように楕円が描かれます。
最小二乗法はシンプルですが精度が低く、点群が楕円の一部しかカバーしていない場合、想定の形状より小さくて平坦な楕円になりやすいです。
Error and covariance matrix
最小二乗法の精度が低い理由は、データの誤差について全く考慮していないからです。そこで、誤差について書いていきます。データxα, yαは、その真値xαˉ,yαˉに誤差△x, △yを加えたものとして、次のように書くことができます。
x_\alpha=\bar{x_\alpha}+\triangle x,y_\alpha=\bar{y_\alpha}+\triangle y...(9)
これらをξαに代入すると、次のようになります。
\xi_\alpha=\bar{\xi_\alpha}+\triangle_1\xi_\alpha+\triangle_2\xi_\alpha...(10)
ここでξαˉは真の値、△1ξαと△2ξαはそれぞれ1次と2次の誤差項です。これを展開すると次のようになります。
\triangle_1\xi_\alpha=\begin{pmatrix}
2\bar{x_\alpha}\triangle x_\alpha \\
2\triangle x_\alpha\bar{y_\alpha}+2\bar{x_\alpha}\triangle y_\alpha \\
2\bar{y_\alpha}\triangle y_\alpha \\
2f_0\triangle x_\alpha \\
2f_0\triangle y_\alpha \\
0 \\
\end{pmatrix},
\triangle_2\xi_\alpha=\begin{pmatrix}
\triangle x_\alpha^2 \\
2\triangle x_\alpha y_\alpha \\
\triangle y_\alpha^2 \\
0 \\
0 \\
0 \\
\end{pmatrix}...(11)
誤差△xαと△yαを確率変数と考えると、ξαの共分散行列は次のように定義されます。
V[\xi_\alpha]=E[\triangle_1\xi_\alpha\triangle_1\xi_\alpha^T]...(12)
Eは分布の期待値を表します。もし△xαと△yαが期待値0、標準偏差σの正規分布に従うとすれば、互いに独立で次の式が成り立ちます。
E[\triangle x_\alpha]=E[\triangle y_\alpha]=0, E[\triangle x_\alpha^2]=E[\triangle y_\alpha^2]=\sigma^2, E[\triangle x_\alpha\triangle y_\alpha]=0...(13)
式(11)を用いると、式(12)は以下のように書けます。
V[\xi_\alpha]=\sigma^2V_0[\xi_\alpha], V_0[\xi_\alpha]=4\begin{pmatrix}
\bar{x_\alpha}^2 & \bar{x_\alpha}\bar{y_\alpha} & 0 & f_0\bar{x_\alpha} & 0 & 0 \\
\bar{x_\alpha}\bar{y_\alpha} & \bar{x_\alpha}^2+\bar{y_\alpha}^2 & \bar{x_\alpha}\bar{y_\alpha} & f_0\bar{y_\alpha} & f_0\bar{x_\alpha} & 0\\
0 & \bar{x_\alpha}\bar{y_\alpha} & \bar{y_\alpha}^2 & 0 & f_0\bar{y_\alpha} & 0 \\
f_0\bar{x_\alpha} & f_0\bar{y_\alpha} & 0 & f_0^2 & 0 & 0 \\
0 & f_0\bar{x_\alpha} & f_0\bar{y_\alpha} & 0 & f_0^2 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 \\
\end{pmatrix}...(14)
すべての要素にσ² が掛けられているので、それを除いてV0[ξα]と書き、正規化共分散行列と呼びます。共分散行列V[ξα]の対角要素は、式(2)の各要素がどれだけ誤差を起こしやすいかを表し、非対角要素は2つの要素間の相関を表します。式(12)の共分散行列は△1ξαのみを用いていますが、△2ξαを加えても、その後の結果にほとんど影響を与えないことが知られています。これは△2ξαが△1ξαに比べて極めて小さいためです。また、式(14)のV0[ξα]は真の値x,yを用いていますが、実際の計算では観測値xαˉ,yαˉに置き換えられています。これも結果にはほとんど影響しません。
以下では、誤差の統計的性質を考慮して、最小二乗法の精度を向上させる様々な方法を示します。
Solution2: Iterative reweight
1. θ0=0,Wα=1(α=1,…,N)と定義する
2. 次の6x6行列Mを計算する
M=\frac{1}{N}\sum_{\alpha=1}^NW_\alpha\xi_\alpha\xi_\alpha^\intercal...(15)
3. 固有値問題を解き、最小固有値λの単位固有ベクトルθを計算する
M\theta=\lambda\theta...(16)
4. 符号を除いてθ≒θ0ならθを返す。そうでなければ、Wαとθ0を更新した後、再度step2を行う。
W_\alpha\leftarrow\frac{1}{(\theta,V_0[\xi_\alpha]\theta)},\theta_0\leftarrow\theta...(17)
統計学によれば、重みWαを各項の分散の逆数に比例させるのが最適であることが知られています(誤差の小さい項ほど大きく、誤差の大きい項ほど小さくなる)。
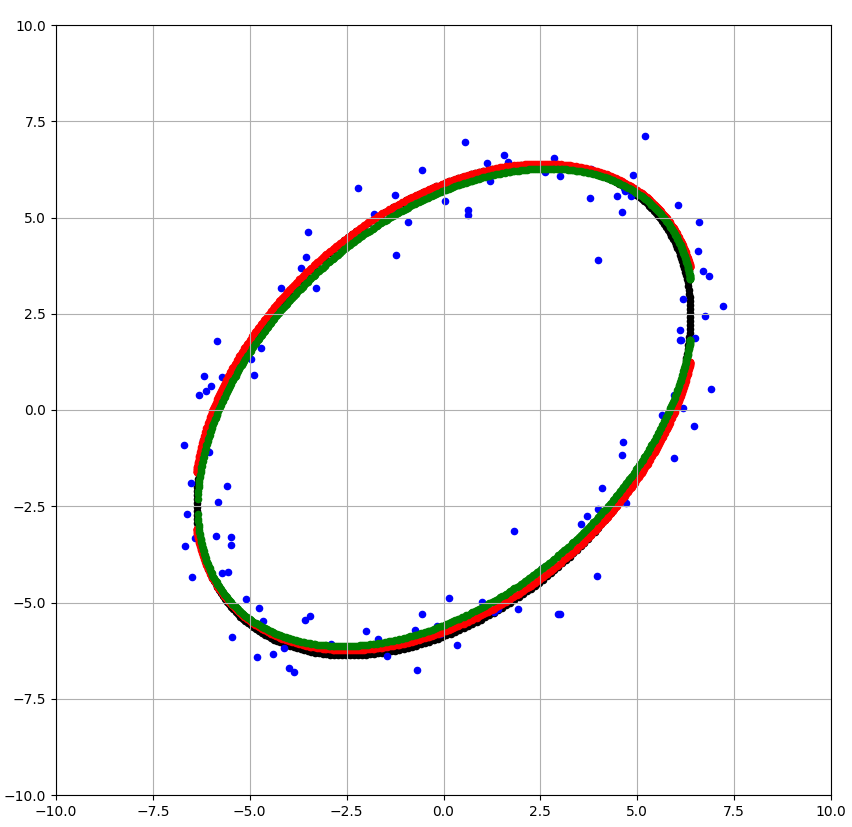
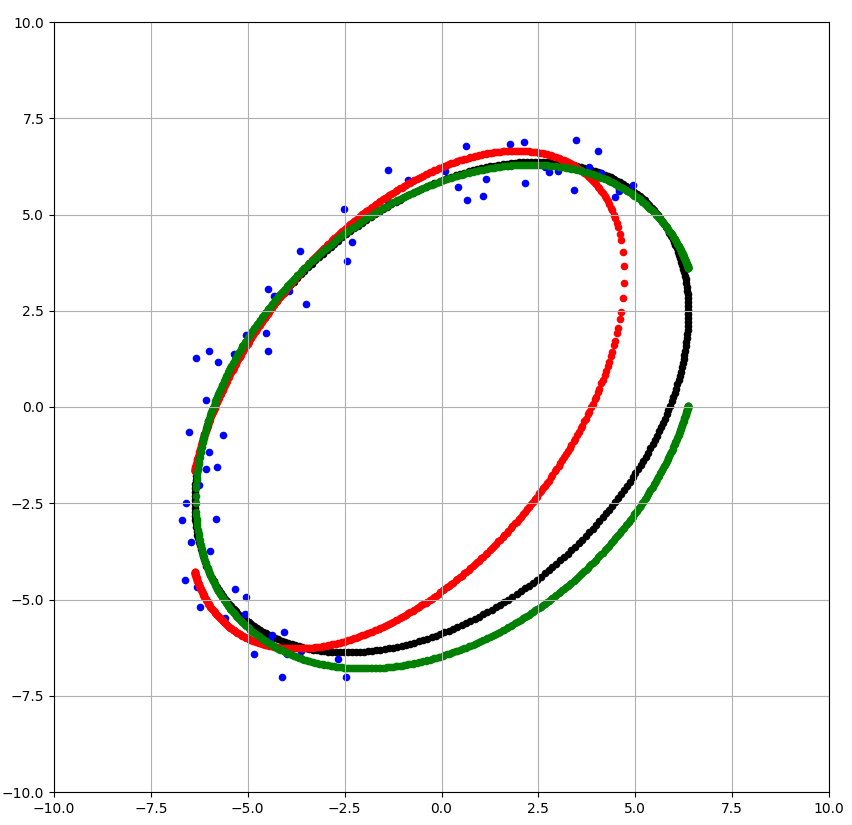
一連の処理を試せるpythonコードはこちらです。実行結果である下画像の各点について説明します。
- 青点は誤差を含んだ点
- 黒点は真値
- 赤点は最小二乗法による推定楕円
- 緑点は重み反復法による推定楕円
Solution3: Renormalization
1. θ0=0,Wα=1(α=1,…,N)と定義する
2. 次の6x6行列Mを計算する
M=\frac{1}{N}\sum_{\alpha=1}^NW_\alpha\xi_\alpha\xi_\alpha^\intercal, N=\frac{1}{N}\sum_{\alpha=1}^NW_\alpha V_0[\xi_\alpha]...(18)
3. 固有値問題を解き、最小固有値λの単位固有ベクトルθを計算する
M\theta=\lambda N\theta...(19)
4. 符号を除いてθ≒θ0ならθを返す。そうでなければ、Wαとθ0を更新した後、再度step2を行う。
W_\alpha\leftarrow\frac{1}{(\theta,V_0[\xi_\alpha]\theta)},\theta_0\leftarrow\theta...(20)
くりこみ法は、当てはめる楕円弧が短い場合の精度の悪さを改善する方法です。
式(19)の形の一般的な固有値問題を解くプログラムツールは通常、Nが正値の対称行列であることを仮定していますが、式(14)からわかるように、V0[ξα]は正値ではないので、Nは正値ではありません。しかし、式(19)は次のように書き換えることができます。
N\theta=\frac{1}{\lambda}M\theta...(21)
データに誤差があってもMは正値対称行列なので、プログラムツールを適用できます。よって、最大の一般固有値1/λに対する単位一般固有ベクトルθが計算できます。
一連の処理を試せるpythonコードはこちらです。実行結果である下画像の各点について説明します。
- 青点は誤差を含んだ点。途中で楕円弧が欠けている。
- 黒点は真値
- 赤点は重み反復法による推定楕円
- 緑点はくりこみ法による推定楕円
Solution4: FNS(Fundamental Numerical Scheme) method
1. θ0=0,Wα=1(α=1,…,N)と定義する
2. 次の6x6行列M,Lを計算する
M=\frac{1}{N}\sum_{\alpha=1}^NW_\alpha\xi_\alpha\xi_\alpha^\intercal, L=\frac{1}{N}\sum_{\alpha=1}^NW_\alpha^2(\xi_\alpha,\theta)^2 V_0[\xi_\alpha]...(22)
3. M−Lを行列Xとして定義する
X=M-L...(23)
4. 固有値問題を解き、最小固有値λの単位固有ベクトルθを計算する
X\theta=\lambda\theta...(24)
5. 符号を除いてθ≒θ0ならθを返す。そうでなければ、Wαとθ0を更新した後、再度step2を行う。
W_\alpha\leftarrow\frac{1}{(\theta,V_0[\xi_\alpha]\theta)},\theta_0\leftarrow\theta...(25)
FNS法は、幾何学的距離を表すサンプソン誤差Jに対して勾配が0となるθを計算します。
J=\frac{1}{N}\sum_{\alpha=1}^N\frac{(\xi_\alpha,\theta)^2}{(\theta,V_0[\xi_\alpha]\theta)}...(26)
\triangledown_\theta J=2(M-L)\theta=2X\theta...(27)
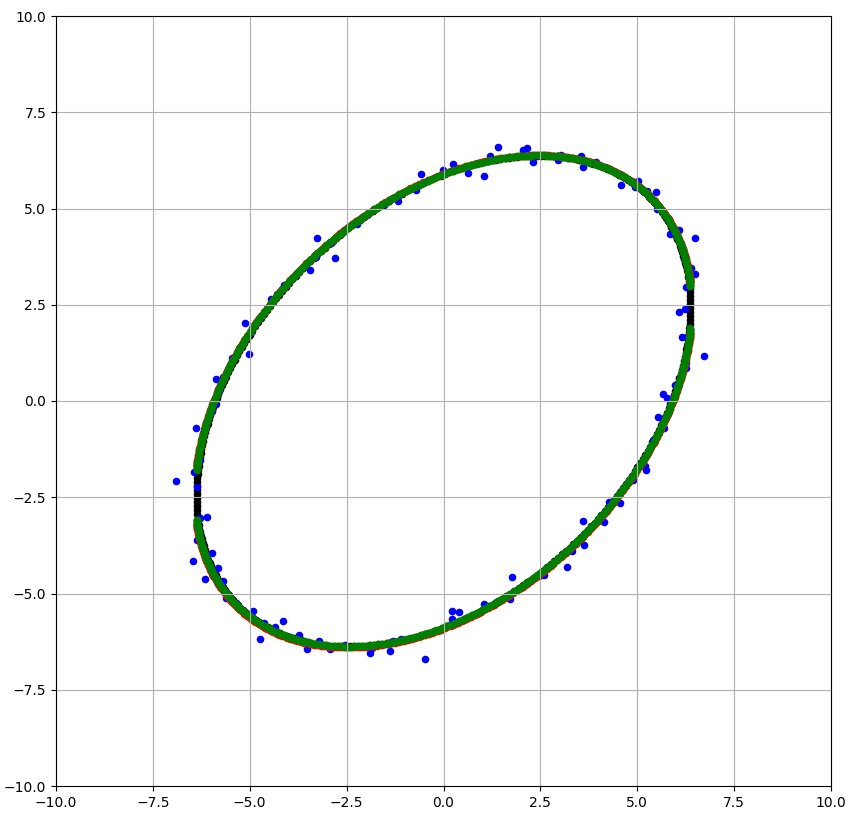
一連の処理を試せるpythonコードはこちらです。実行結果である下画像の各点について説明します。
- 青点は誤差を含んだ点
- 黒点は真値
- 緑点はFNS法による推定楕円
Solution5: Robust fitting by RANSAC
実際の画像は、必ずしも楕円上の点だけで構成されているとは限らず、他の物体の境界が含まれている場合もあります。このような楕円を形成しない点をアウトライア(外れ値)と呼びます。一方、楕円を形成する点をインライアと呼びます。アウトライアの影響を受けにくい当てはめをRobust fittingと呼びます。代表的な手法にRANSAC(Random Sample Consensus)があります。RANSACは楕円当てはめに限らず、様々なタスクでデータの外れ値を除去したい時に使えるので、かなり有用です。
1. 入力点群からランダムに5点を選択し、ξ1,...,ξ5を式(2)のベクトルとする
2. 固有値問題を解き、最小固有値λの単位固有ベクトルθを計算する
M_5=\sum_{\alpha=1}^5\xi_\alpha\xi_\alpha^\intercal...(28)
3. 求めた楕円θについて、以下の式を満たす入力点群の数(n)を数える
dは閾値として決めておきます。
\frac{(\xi_\alpha,\theta)^2}{(\theta,V_0[\xi_\alpha]\theta)} < d^2...(29)
4. 入力点群から別の5点をランダムに選択し、同じ操作を行う。これを何度も繰り返し、楕円の候補の中からnが最大のものを選ぶ。
5. 最終的に選択された楕円について、式(29)を満たさない点はアウトライアとみなし、除去する
一連の処理を試せるpythonコードはこちらです。実行結果である下画像の各点について説明します。
- 青点はアウトライアとみなされた点
- 赤点はインライアとみなされた点
- 黒点は真値
- 緑点はRANSACでアウトライアが除かれた点群でFNS法を用いた推定楕円