Python数学シリーズ③ 行列式(置換)

このシリーズについて

数学の理解を深めるためにpythonで実装しながら、理解を進めてます。当分は線形代数やろうと思います。数学はそんなに好きではありませんでしたが、最近好きになってきたかもしれません。シリーズの目次はこちら。

行列式と置換

行列式は以下の式で定義されます。参照元

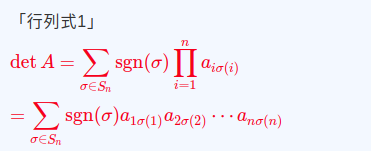
いきなり、行列式を実装しようとしても色々と知識が足りなかったので、とりあえず置換をまずやっていこうと思います。
置換は以下のように定義されます。参照元

(1, 2, 3)とかだと(3, 1, 2)とかが置換されたものの例になります。n文字の置換は全部でn!通りあることになります。今回は置換の積を実装していこうと思います。
置換の積は以下のように表されます。参照元

こちらの記事いわく、2つの置換の対応関係（「A→B」と「B→C」）を3段論法的な感じで1つにギュッとまとめる(「A→C」)感じだそうです。詳しく突き詰めると、自分の場合沼にはまりそうなのでこのイメージでとどめておきます。今回はこの置換の積を実装していこうと思います。

置換の積

置換の積ができるpythonのライブラリが見つからなかったので、自分の実装が合っているか不安です。もしライブラリがあれば教えてください。下のような感じで実装してみました。シンプルに定義どおりにやってみました。

def permutation(list1, list2):
	list_len = len(list2[1])
	final_list = []
	first_list = []
	ans_list = []
	for i in range(list_len):
		a = list2[1][i]
		ans = list1[1][a - 1]
		if list1[0][i] != ans:
			first_list.append(list1[0][i])
			ans_list.append(ans)
	final_list.append(first_list)
	final_list.append(ans_list)
	return final_list

def main():
	print("~~permutation_test~~")
	pm1 = [[1, 2, 3], [2, 3, 1]]
	pm2 = [[1, 2, 3], [3, 2, 1]]
	print("my_answer:", permutation(pm1, pm2))
    # 出力結果
    # ~~permutation_test~~
    # my_answer: [[2, 3], [3, 2]]

これは改善の余地が大いにありそうですが、とりあえずこんな感じで今回はやってみました。

まとめ

大学の数学の授業、予備のりたくみの動画でいい説。

間違いや質問、ご意見等ありましたらお気軽にコメントください。頑張って答えますので(笑)。