Abstract
360度カメラでよく使われているEquirectangular画像上の座標を、球面上の3次元座標に変換することは、カメラと対象物の位置関係を知る上でかなり重要です。ここではその方法をまとめます。
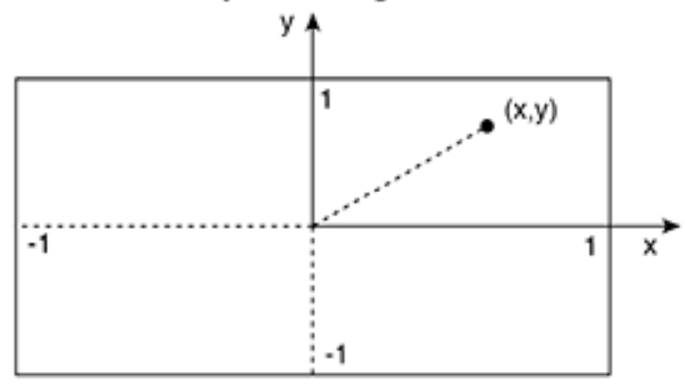
イメージとしては、下画像のようなEquirectangular画像上の座標から

球面座標に変換します。
Algorithm
1. Equirectangular画像座標を正規化する
座標の原点が左上にある場合は次のような変換で、正規化を行うことができます。
\begin{align}
center_x &= equi_x-width/2 + 0.5 \\
center_y &= (-1)\times equi_y+height/2+0.5 \\
norm_x &= center_x/(width/2-0.5) \\
norm_y &= center_y/(height/2-0.5)
\end{align}
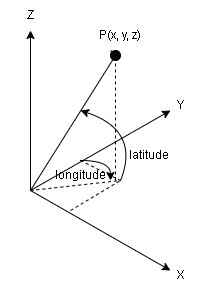
2. 経度と緯度を計算する
ここでは経度と緯度と言っていますが、ヨーとピッチのことです。正規化されたx, yの値は-1~1をとるので、経度の場合は$π$、緯度の場合は$π/2$ をx,yに掛けることで求めることができます。
\begin{align}
longitude &= norm_x\times\pi \\
latitude &= norm_y\times\frac{\pi}{2}
\end{align}
3次元ベクトルを計算する
経度と緯度を用いて、半径1の球面座標を計算します。
\begin{align}
x &= cos(latitude)\times sin(longitude) \\
y &= cos(latitude)\times cos(longitude) \\
z &= sin(latitude)
\end{align}
Code
全体のコードはこちらです。 equirectangular_to_sphere.py を実行すれば試すことができます。
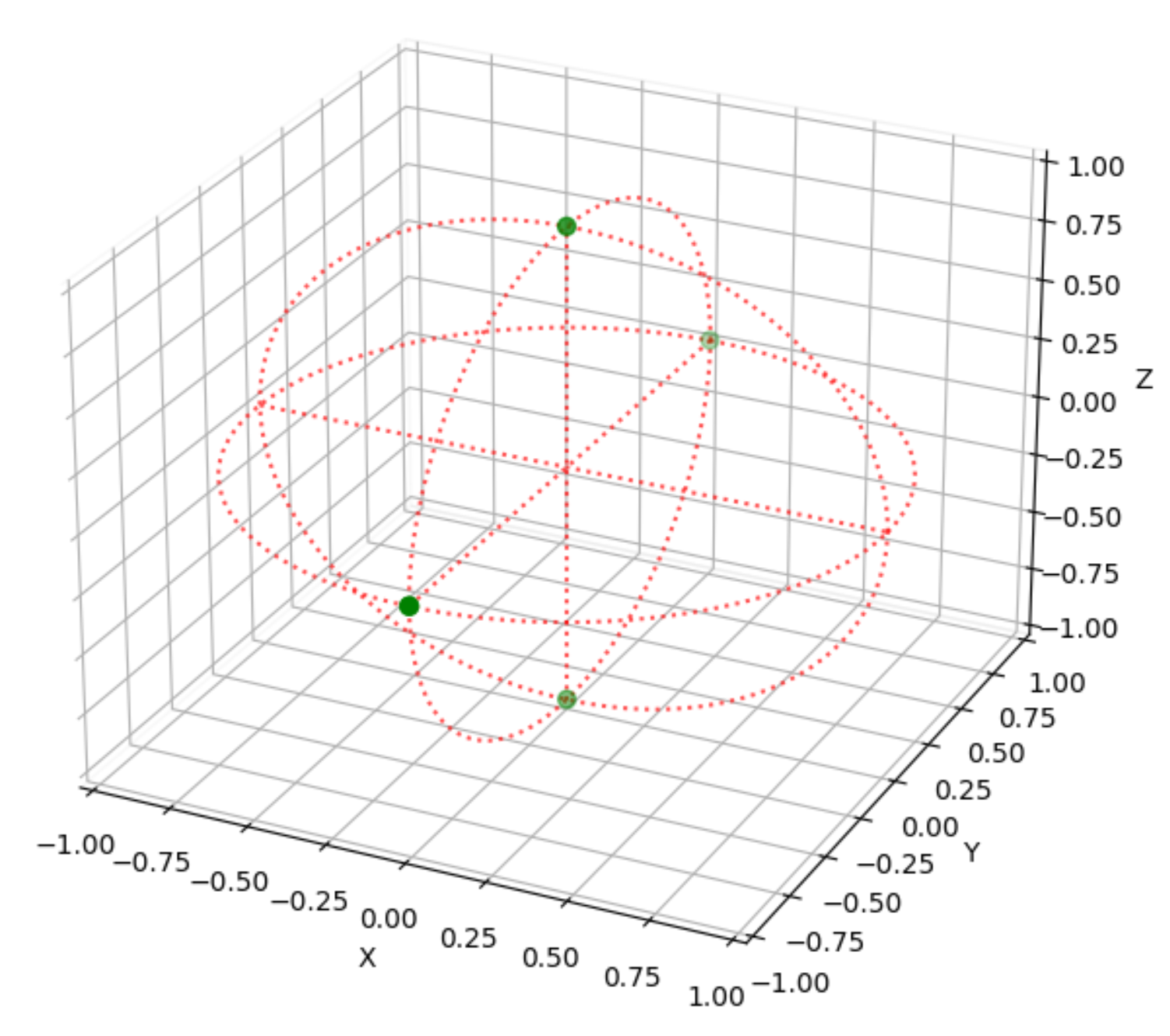
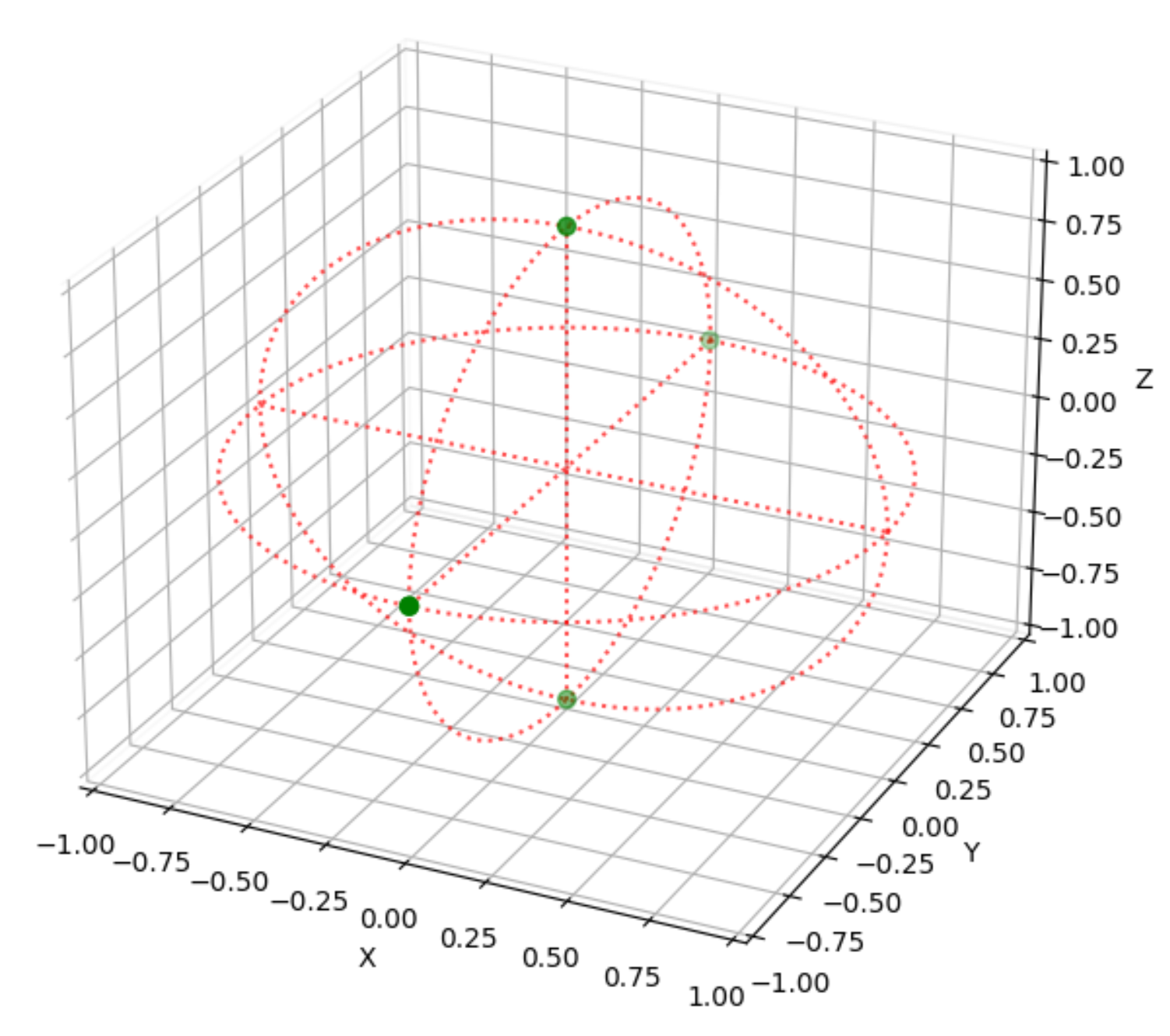
Equirectaungular画像座標での各点([0, height/2–1], [width/2–1, 0], [width/2–1, height/2–1], [width/2–1, height-1], [width-1, height/2–1]) は、下画像のような球面座標(緑点)に変換されます。