概要
3次元点群を扱う際、主成分分析を使うと色々便利なんだ、と最近知りました。今回は主成分分析を使った3次元点群の方向の解析についてまとめていきます。ちなみに、主成分分析して得た情報は、点群データの特徴量としても利用されます。詳しくはこちら。
主成分分析について
主成分分析によって、N次元のデータについて、それぞれの次元の散らばりの大きさや、その方向性を得ることができます。機械学習などでは、そのデータの特徴をより表している次元だけを残す次元圧縮などに使われています。
手順
それでは、3次元データを主成分分析する手順を示します。
1. 点群の平均を求めて、元の点群から平均を引いた行列を求める
c=\frac{1}{n}\sum_{i=1}^{n}p_i
M=[p1 − c, . . . , pn − c]
2. Mの共分散行列を求める
C=M^\intercal M
3. 共分散行列Cを固有値分解する
C=P\Lambda P^{-1} (\Lambda=diag(\lambda_1,\lambda_2,\lambda_3))
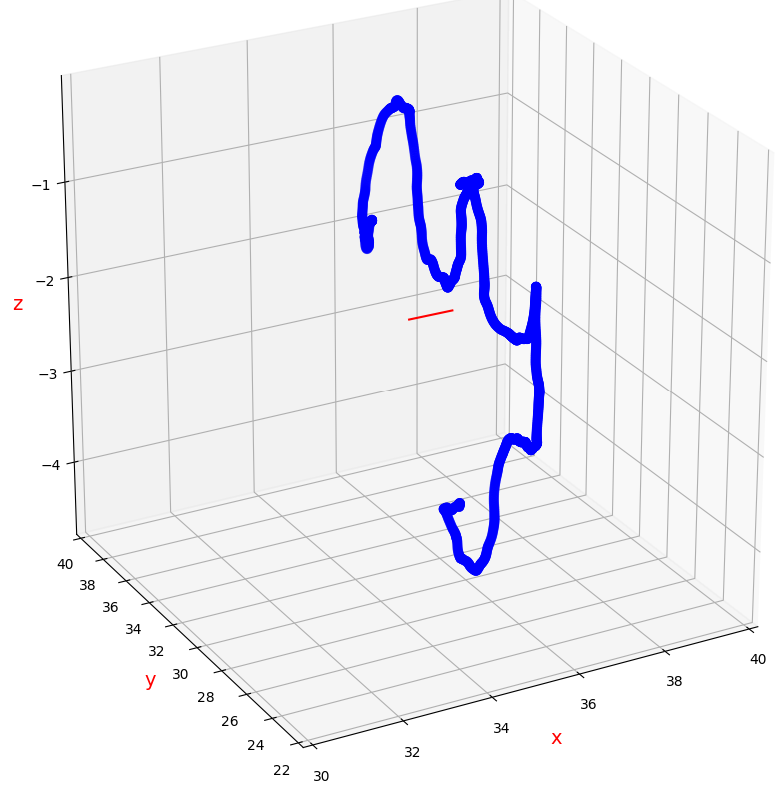
固有値が大きいほど、その固有値に対する固有ベクトルの方向への散らばりも大きくなります。一番小さい固有値に対する固有ベクトルは、点群データの法線ベクトルになります。以下の画像での赤線が青色の点群の法線ベクトルです。
おまけ
上で求めた固有値の大きさを比較することで、点群データがどのような形状をしているのか(次元特徴)を把握することができます。σを以下のように置いて、
\sigma_1=\lambda_1-\lambda_2,\sigma_2=\lambda_2-\lambda_3,\sigma_3=\lambda_3
その中の最大値を求めます。
d=argmax(\sigma_k)(k=1,2,3)
dの値によって、その点群が線状か面状か、3次元まんべんなく広がっているのかが判定できます。
以下の画像は、点群の点iの近傍点集合N(i)に対する主成分分析を行った後、次元特徴を求めています。線を形成している点は赤色で、面を形成している点は緑色で、3次元まんべんなく広がっている点は青色になっています。

(参照元)
まとめ
共分散行列、何かと出てくる。