はじめに
一般的なECサイトを運営していると、何か施策を打ったらCVRがどうなったとか、クーポンを配布したら売り上げがどう変わったかをチェックすると思います。ですが、「CVR上がったけど偶然じゃない?」とか、「有意でしょ!(なんとなく)」で終わらせてしまうこともあるかもしれません。
この記事では、統計を用いた有意性のチェックについての説明と、jupyter notebookにコピペして使える簡単なツールを載せます。
説明はあまり厳密なものではないです。
対象者
- 統計よく分からない
- python, jupyter notebookは使ったことある
- 理論とか良いからとりあえず有意性調べたい(随所にコピペしてそのまま使えるツールあります。)
CVRのブレ
Aさんの会社では、ウェブサイトでりんごを売っています。Aさんは上司に言われ、CVRを計算することになりました。CVRは売れた数をPVで割ったものです。
その日は1,000PVで30個売れたので、CVRは3.0%でした。
次の日は1,000PVで28個売れたので、CVRは2.8%になってしまい、嘘をついたと上司に怒られてしまいました。
CVRはぶれる物なので、大体合ってるという範囲で伝える必要があります。
とりあえず勘で2.5% ~ 3.5%ということもできますが、もうちょっと統計的に考えたいです。
ここで、ウェブサイトに訪れた人が「買う」か「買わない」かの2択になるような現象を表したものとして、ベルヌーイ分布や二項分布と呼ばれるものがあります。
下のグラフは、横軸に売れた個数、縦軸にそのときの確率を表示しています。30個が一番売れる確率が高くて、20個以下になることはほとんど無さそうですね。
import numpy as np
from scipy.stats import binom, norm
import pandas as pd
p = 0.03
N = 1000
k = np.arange(100)
pd.Series(binom.pmf(k, N, p), name='binom').plot(figsize=(12,6), legend=True)
これがあれば、値が大きめのところをピックアップして、大体合っている範囲を出せそうです。ちなみに、この範囲のことを信頼区間、信頼区間に入る確率のことを信頼係数と呼びます。下のツールを使って、95%の確率で正しくなる範囲を出してみます。(サンプル数がPV数となります。)
# 母比率の信頼区間
import ipywidgets as widgets
import math
from scipy.stats import binom, norm
def calc(v):
input_N = w.value
input_cvr = w2.value
input_conf = w3.value
p = input_cvr / 100
# 二項分布の場合
max_index = binom.isf((100 - input_conf) / 100, input_N, input_cvr / 100)
min_index = binom.isf(input_conf / 100, input_N, input_cvr / 100)
# 正規分布に近似する場合
#max_index = norm.isf((100 - input_conf)/100, loc=input_N*p, scale=np.sqrt(input_N*p*(1-p)))
#min_index = norm.isf(input_conf/100, loc=input_N*p, scale=np.sqrt(input_N*p*(1-p)))
print(f'{math.floor(min_index / input_N * 10000) / 100}(%) <= CVR <= {math.ceil(max_index / input_N * 10000) / 100}(%)')
button = widgets.Button(description="計算")
button.on_click(calc)
w = widgets.IntText(
value=1000,
description='サンプル数:',
disabled=False
)
w2 = widgets.BoundedFloatText(
value=1,
min=0,
max=100.0,
description='CVR(%):',
disabled=False
)
w3 = widgets.BoundedIntText(
value=95,
min=0,
description='信頼係数(%):',
disabled=False
)
output = widgets.Output()
display(w, output)
display(w2, output)
display(w3, output)
display(button, output)
実行すると、下の画像のようになります。自由に入力できるようになっています。
2.11(%) <= CVR <= 3.89(%)となりました!結構広いですね。信頼係数を95->90%にすると、範囲は狭くなります。
「10代~20代、もしくは30代~40代、または50代以上の人物」だと当たる確率が高いのに対し、「10代~20代」なら外れやすくなるような感じです。
サンプル数を大きくしてみると範囲が小さくなったりもします。
ソース中のコメントアウトされている部分は、ベルヌーイ分布を正規分布に近似した場合です。サンプル数が十分大きいとほぼ同じ結果が得られます。
実行してみると、サンプル数が1,000でも十分大きいと言ってよさそうです。
わざわざ近似する必要はないように思えますが、正規分布を仮定すると統計的にやりやすいことが多いです。
CVRの差の検定
商品があまりに売れないので、催眠術の画像をモーダルで出すようにしたところ、CVRが2.0%から3.0%に増加しました。どちらも1,000PVです。
1.5倍に上がったので有意っぽいですが、統計的に検証(=検定)してみます。
検定では、ほとんど起こらないだろうと思ってたのに起こったときに「有意である」と表現します。その確率を有意水準といい、まずこれを先に決めます。
この場合有意水準を5%にすると、2.0->3.0%に上がったということから差があるといえる確率が5%以下なら「有意である」と言えます。
詳細は省きますが、サンプル数が十分に大きいときベルヌーイ分布は正規分布に近似でき、正規分布同士の差も正規分布になることを利用しているので(参考:正規分布の再生性)サンプル数は1,000程度はあったほうが正確な結果になります。
# 母比率の差の検定
import matplotlib.pyplot as plt
import ipywidgets as widgets
import math
from scipy.stats import norm
def calc_plot(v):
input_N1 = w_n1.value
input_cvr1 = w_cvr1.value
input_N2 = w_n2.value
input_cvr2 = w_cvr2.value
input_conf = w3.value
p1 = input_cvr1 / 100
p2 = input_cvr2 / 100
N1 = input_N1
N2 = input_N2
p = (N1 * p1 + N2 * p2) / (N1 + N2)
z = (p2 - p1) / math.sqrt(p * (1 - p) * (1 / N1 + 1 / N2))
min_index = norm.isf(1 - (100 - input_conf)/(2*100), loc=0, scale=1)
max_index = norm.isf((100 - input_conf)/(2*100), loc=0, scale=1)
if min_index <= z and z <= max_index:
print('有意であるとは言えません')
print(f'|{z}| <= {max_index}')
else:
print('有意な差があります!')
print(f'{max_index} <= |{z}|')
xlimit = np.array([math.ceil(abs(z)), 5]).max()
x = np.arange(- xlimit * 100, xlimit * 100)/100
y = norm.pdf(x)
plt.figure(figsize=(15, 7))
plt.vlines([min_index, max_index], y.min(), y.max(), "red", linestyles='dashed', label='rejection')
plt.legend()
plt.vlines([z], y.min(), y.max(), "black", linestyles='dashed', label='statistics')
plt.legend()
plt.plot(x, y,'b-', lw=1, label='norm pdf')
button = widgets.Button(description="計算")
button.on_click(calc_plot)
w_n1 = widgets.IntText(
value=10000,
description='サンプル数:',
disabled=False
)
w_n2 = widgets.IntText(
value=12000,
description='サンプル数:',
disabled=False
)
w_cvr1 = widgets.BoundedFloatText(
value=2,
min=0,
max=100.0,
description='CVR(%):',
disabled=False
)
w_cvr2 = widgets.BoundedFloatText(
value=3,
min=0,
max=100.0,
description='CVR(%):',
disabled=False
)
w3 = widgets.BoundedIntText(
value=95,
min=0,
description='信頼係数(%):',# 100 - 有意水準
disabled=False
)
w_a = widgets.VBox([widgets.Label('A'), w_n1, w_cvr1])
w_b = widgets.VBox([widgets.Label('B'), w_n2, w_cvr2])
whbox = widgets.HBox([w_a, widgets.Label(' '), w_b])
output = widgets.Output()
display(whbox, output)
display(w3, output)
display(button, output)
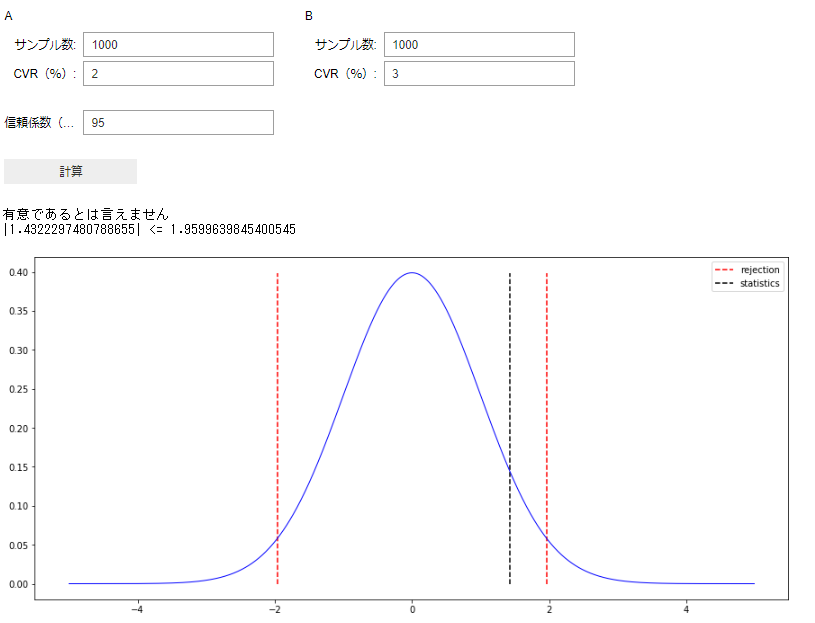
上のコードを実行すると、下の画像のような結果になりました。
二つの赤線の内側に黒線が入っていると「このくらいのブレはありえるよね」とみなされて有意であると言えない結果になります。
逆に外側にあれば有意であると言えます。
しばらくA/Bテストの様子見をしていって、どちらも10,000PVで2.0%->3.0%に増えている場合は有意な差といえるようになります。
サンプル数が増えることでブレが小さくなったのに1.0%も違うのは偶然じゃないということですね。
ここで注意したいのは、「有意であるとは言えない」からといって有意でないと結論付けることはできないということです。
また、黒線と赤線がめちゃくちゃ離れているからといってとても有意、非常に有意とはなりません。有意かどうかの2択です。
そう考えると検定の結果よりも信頼区間の方が多く情報を持っているような気がします。
AよりBのほうが大きいかどうか
上の場合では差があるかどうかを検定していましたが、実際は施策を行ってCVRが上がったかどうかだけを知りたいのが普通だと思います。
その場合は、片側検定を使います。(上の場合は両側検定と呼びます。)
片側検定をする際には、上のpythonコードの中のcalc_plotを下のコードで置き換えます。
input_N1 = w_n1.value
input_cvr1 = w_cvr1.value
input_N2 = w_n2.value
input_cvr2 = w_cvr2.value
input_conf = w3.value
p1 = input_cvr1 / 100
p2 = input_cvr2 / 100
N1 = input_N1
N2 = input_N2
p = (N1 * p1 + N2 * p2) / (N1 + N2)
z = (p2 - p1) / math.sqrt(p * (1 - p) * (1 / N1 + 1 / N2))
max_index = norm.isf((100 - input_conf)/100, loc=0, scale=1)
if z <= max_index:
print('有意であるとは言えません')
print(f'|{z}| <= {max_index}')
else:
print('有意な差があります!')
print(f'{max_index} <= |{z}|')
xlimit = np.array([math.ceil(abs(z)), 5]).max()
x = np.arange(- xlimit * 100, xlimit * 100)/100
y = norm.pdf(x)
plt.figure(figsize=(15, 7))
plt.vlines([max_index], y.min(), y.max(), "red", linestyles='dashed', label='rejection')
plt.legend()
plt.vlines([z], y.min(), y.max(), "black", linestyles='dashed', label='statistics')
plt.legend()
plt.plot(x, y,'b-', lw=1, label='norm pdf')
この場合は、赤線より右側に黒線があれば有意だと言えます。こちらの方が上かどうかしか見ない分、少ないサンプルで有意判定が出やすくなります。
平均購入金額の信頼区間
CVRが上がっていても平均購入金額が下がっている可能性があるかもしれません。(クーポンを配布した際に最低利用金額ギリギリの購入が増えた場合など)
平均購入金額のブレがどのくらいあるのか計算してみます。
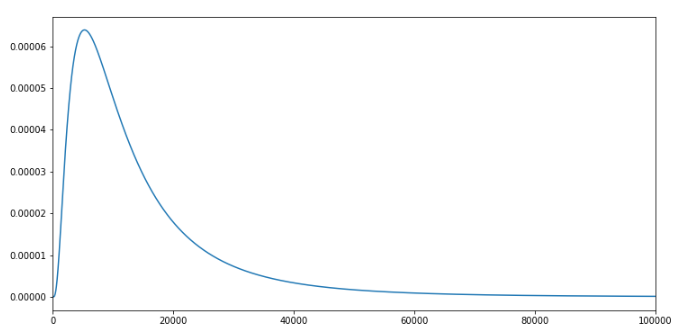
一般的に年収は対数正規分布になっており、年収と購入金額に正の相関があるので、いろんな商品を取り扱うECサイトでは購入金額もそれに近い分布をしていると考えられます。
(参考:対数正規分布の例と平均,分散)
# 対数正規分布
from scipy.stats import lognorm
x = np.arange(1, 100000) / 1
A = 1.5000e+04 # 平均購入金額
B = 1.5000e+04 ** 2 # 分散
s = np.sqrt(np.log(B/(A ** 2) + 1))
mu = np.log(A) - (s ** 2 / 2)
y = pd.Series(lognorm.pdf(x, s, 0, np.exp(mu)))
y.index = x
y.plot(figsize=(12, 6))
これを合わせて平均をとると、また正規分布になります。
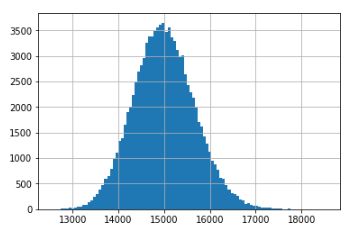
下のコードは500個の平均を計算する、という操作を十万回繰り返した結果のヒストグラムです。
中心極限定理によって、別に対数正規分布じゃなくても十分なサンプルがあれば平均のヒストグラムは似たような形になります。
十分なサンプルがどのくらいかというのは分布によって変わりますが、大体1,000もあれば良さそうです。
means = []
n = 500
for i in range(0, 100000):
means.append(np.array(lognorm.rvs(s, 0, np.exp(mu), size=n)).mean())
pd.Series(means).hist(bins=100)
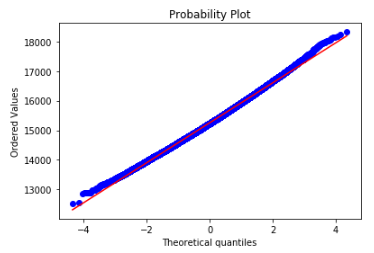
下の画像はQ-Qプロットと呼ばれるもので、青が赤の直線に近ければ正規分布に近いといえるものです。
import pylab
stats.probplot(means, dist="norm", plot=pylab)
下のコードで、正規分布の信頼区間を計算します。今回の「サンプル数」はPVではなく、購入数です。
# 平均購入金額の信頼区間
import ipywidgets as widgets
import math
import numpy as np
import pandas as pd
from scipy.stats import binom, norm
def calc(v):
n = w.value
mu = w2.value
sigma = w3.value
input_conf = w4.value
max_index = norm.isf((100 - input_conf)/100, loc=mu, scale=sigma / np.sqrt(n))
min_index = norm.isf(input_conf/100, loc=mu, scale=sigma / np.sqrt(n))
print(f'{min_index} <= 平均購入金額 <= {max_index}')
button = widgets.Button(description="計算")
button.on_click(calc)
w = widgets.IntText(
value=1000,
description='サンプル数:',
disabled=False
)
w2 = widgets.FloatText(
value=15000,
description='平均購入金額:',
disabled=False
)
w3 = widgets.FloatText(
value=15000,
description='標準偏差:',
disabled=False
)
w4 = widgets.BoundedIntText(
value=95,
min=0,
description='信頼係数(%):',
disabled=False
)
output = widgets.Output()
display(w, output)
display(w2, output)
display(w3, output)
display(w4, output)
display(button, output)
売上の信頼区間
売上=PV数×CVR×平均購入金額
なので、CVR×平均購入金額の信頼区間を掛け合わせて出します。
# 売上の信頼区間
import ipywidgets as widgets
import math
from scipy.stats import binom, norm
def calc(v):
n = w_n.value
cvr = w_cvr.value
mu = w_mu.value
sigma = w_s.value
input_conf = w_conf.value
p = cvr / 100
min_index_sales = norm.isf(1 - (100 - input_conf)/(2*100), loc=mu, scale=sigma / np.sqrt(n*p))
max_index_sales = norm.isf((100 - input_conf)/(2*100), loc=mu, scale=sigma / np.sqrt(n*p))
max_index = norm.isf((100 - input_conf)/100, loc=n*p, scale=np.sqrt(n*p*(1-p))) / n
min_index = norm.isf(input_conf/100, loc=n*p, scale=np.sqrt(n*p*(1-p))) / n
print(f'{n * min_index * min_index_sales} <= 売上 <= {n * max_index * max_index_sales}')
button = widgets.Button(description="計算")
button.on_click(calc)
w_n = widgets.IntText(
value=10000,
description='サンプル数(PV):',
disabled=False
)
w_cvr = widgets.BoundedFloatText(
value=12.4,
min=0,
max=100.0,
description='CVR(%):',
disabled=False
)
w_mu = widgets.FloatText(
value=18303,
description='平均:',
disabled=False
)
w_s = widgets.FloatText(
value=15217,
description='標準偏差:',
disabled=False
)
w_conf = widgets.BoundedIntText(
value=90,
min=0,
description='信頼係数(%):',
disabled=False
)
output = widgets.Output()
display(w_n, output)
display(w_cvr, output)
display(w_mu, output)
display(w_s, output)
display(w_conf, output)
display(button, output)
本当はCVRと平均購入金額が独立であるとは限りません。
平均購入金額が上がるとCVRが下がる関係にあるとすると、信頼区間はもっと狭くなりそうな気もします。
そこまで細かく検証する前に力尽きてしまいました……。