銀行のWebサイトで住宅ローンのシミュレーションを行うと、35年のローンの詳細な内容が一瞬で返ってきます。多くの場合、元利均等方式という、利息と元金を合わせて毎月の支払額が一定になるような方式で返済していくわけですが、なかなか複雑です。
以下は見栄えのために極端に利率を上げて描いたグラフですが、こんなイメージになります。
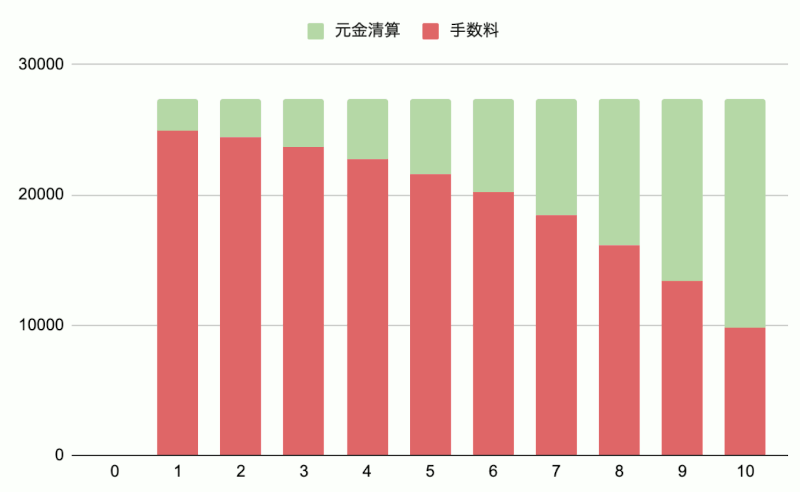
1ヶ月目は、元金全額 * 実質年率 * 1ヶ月分の利息がかかります。利息から優先的に支払うため、月々の支払額のうち残りの枠を元金の清算に充てます。
2ヶ月目は、残りの元金 * 実質年率 * 1ヶ月分の利息がかかります。1ヶ月目に元金が減ったので、利息も少し安くなっています。元金の減るスピードが上がっていきます。
...
nヶ月目に、元金すべてが支払い終わります。
このレベルであれば、銀行等で説明されていることでしょう。
では、月々いくら支払えば元利均等でピッタリn回で支払い終わるのでしょうか? 数字を当てはめながら調整していったのではとても大変です。
いくつか前提がありますが、元利均等方式には数学の公式が存在し、公式に当てはめれば月々の支払額は簡単に計算することができます。
ローンの公式
- 元金$a$
- 月利$s$ (実質年率を12で割ったもの)
- 月々の支払額 $x$
- 支払回数 $n$
こんな関係が成り立ちます。
$$
x = \frac{as}{1-(1+s)^{-n}}
$$
例えば10万円を10回払い、実質年率15%(=月利だと1.25%)だと、おおよそ 10,700円/月 となります。
$$
x = \frac{100000 * 0.0125}{1 - 1.0125^{-10}} = 10700.30...
$$
なお、この公式はExcelやSpreadsheet等の表計算ソフトウェアにはPMTという財務関数として組み込まれています。 =-PMT(0.0125, 10, 100000, 0, 0) みたいな感じで同じ値を求められます。同等の結果を返すOSSライブラリもいくつか見つかったので、コード的な実装方法が知りたい人はお好みのプログラミング言語で探してみるとよいでしょう。
「月利」や「月々の支払額」などと書きましたが、正確には支払い期間ごとの利率にそろえてあれば期間は自由です。年1回払いであればsには実質年率をそのまま与えると良いです。
この公式は、以下の前提を持ちます。
- 月の日数は考慮しない。1ヶ月=1年/12とする
- 月末に購入し、翌月末から毎月末日に返済していくとする
- つまり、最初の返済は元金x1ヶ月分の利息がかかっている状態から始まる
- 元利均等返済とする
- 利息 → 元金の順に充当する (もしくは、複利とみなす)
ローンの公式の導出
導出方法は色々あるようです。高校数学程度の知識で解けます。
- 愚直に展開していき、等比数列の和の公式を適用する方法
- 隣接二項間漸化式にして一般項を求める方法
- 割引現在価値を使う方法
(1)愚直に展開していき、等比数列の和の公式を適用する方法
1ヶ月目に返済した直後の残元金は、aに(1+s)を掛けて、月々の支払額xを引いた値になる。
$$
a_1 = a(1 + s) - x
$$
2ヶ月目に返済した直後の残元金は、a_1に更に(1+s)を掛けて、月々の支払額xを引いた値になる。
$$
a_2 = a_1(1 + s) - x
$$
a_1を代入すると、
$$
\begin{eqnarray}
a_2 &=& (a(1+s) - x)(1+s) - x \\
&=& a(1+s)^2 - x(1+s) - x
\end{eqnarray}
$$
同様にa_3を計算すると
$$
\begin{eqnarray}
a_3 &=& (a(1+s)^2 - x(1+s) - x)(1+s) - x \\
&=& a(1+s)^3 - x(1+s)^2 -x(1+s) - x \\
\end{eqnarray}
$$
同様にa_4を計算すると
$$
\begin{eqnarray}
a_4 &=& (a(1+s)^3 - x(1+s)^2 - x(1+s) -x)(1+s) - x \\
&=& a(1+s)^4 - x(1+s)^3 -x(1+s)^2 -x(1+s) - x \\
\end{eqnarray}
$$
こうしてみると、法則性があることが見えてくる。kヶ月目の返済後の残元金は以下のようになる。
$$
\begin{eqnarray}
a_k &=& a(1+s)^{k} - x((1+s)^{k-1} + (1+s)^{k-2} + ... + (1+s)^1 + 1)
\end{eqnarray}
$$
xにかかっている部分は、初項1、公比(1+s)の等比数列のうち、第k項までの和の形式になっている。
等比数列の和の公式をあてはめると、
$$
S{n}=\frac{a(r^n-1)}{r-1}
$$
$$
1 + (1+s) + (1+s)^2 + ... + (1+s)^{k-1}
= \frac{(1+s)^k - 1}{(1+s) - 1}
= \frac{(1+s)^k - 1}{s}
$$
よってa_kは
$$
a_k = a(1+s)^k - x\frac{(1+s)^k - 1}{s}
$$
nヶ月後の支払い後、残元金が0になればよいので、
$$
a_n = 0 = a(1+s)^n - x\frac{(1+s)^n-1}{s}
$$
これをxについて整理していくと
$$
\begin{eqnarray}
x &=& \frac{as(1+s)^n}{(1+s)^n - 1} \\
x &=& \frac{as}{1 - (1+s)^{-n}}
\end{eqnarray}
$$
これでローンの公式が導出できた。
(2)隣接二項間漸化式にして一般項を求める方法
kヶ月目の支払い直後の残債を $a_k$ とおくと、前月支払い後の残債 $a_{k-1}$ を使って、こんな感じの式で表せる。
$$
a_k = a_{k-1} (1 + s) - x
$$
初項は1ヶ月後の残債。借りた金額 a に利息 as を足して月々の返済額 x を引いたものになるから、
$$
a_1 = a(1 + s) - x
$$
この隣接二項間漸化式を一般項に直す。
等比数列 $a_k-\alpha = (1+s)(a_{k-1}-\alpha)$ の形にすることを考える。
この式を展開して整理していくと、
$$
\begin{eqnarray}
a_k - \alpha &=& (1+s)(a_{k-1}-\alpha) \\
&=& a_{k-1}-\alpha +sa_{k-1}-s\alpha \\
a_k &=& a_{k-1}(1+s) - s\alpha
\end{eqnarray}
$$
漸化式と見比べると、$-s\alpha = -x$ となることがわかる。よって $\alpha = x/s$
元の式 $a_k = a_{k-1} (1 + s) - x$は、 $a_k-x/s = (1+s)(a_{k-1}-x/s)$ と変形できることがわかる。
ここで、$b_k = a_k - x/s$ とおくと、$b_k = (1+s)b_{k-1}$
初項は
$$
\begin{eqnarray}
b_1 &=& a_1 - \frac{x}{s}\\
&=& a(1+s)-x -\frac{x}{s}\\
&=& a(1+s)-\frac{x}{s}(1+s)\\
&=& \left(a-\frac{x}{s}\right)(1+s)
\end{eqnarray}
$$
数列$b_k$は、公比$(1+s)$の等比数列となるから、等比数列の一般項の公式を$a_k = a_1r^{k-1}$を使って
$$
\begin{eqnarray}
b_k &=& \left(a-\frac{x}{s}\right)(1+s)(1+s)^{k-1}\\
&=&\left(a-\frac{x}{s}\right)(1+s)^k
\end{eqnarray}
$$
$b_k=a_k-x/s$ なので、代入すると
$$
\begin{eqnarray}
a_k - \frac{x}{s} &=& \left(a-\frac{x}{s}\right)(1+s)^k\\
a_k &=& \left(a-\frac{x}{s}\right)(1+s)^k + \frac{x}{s}
\end{eqnarray}
$$
これで数列$a_k$の一般項がわかった。
n回目の返済で残債が0になればよいので、$a_n = 0$
$$
\begin{eqnarray}
a_n = 0 &=& \left(a - \frac{x}{s}\right)(1+s)^n + \frac{x}{s}\\
&=& a(1+s)^n - \frac{x}{s}(1+s)^n + \frac{x}{s}\\
x\frac{(1+n)^n-1}{s} &=& a(1+s)^n \\
x &=& \frac{as(1+s)^n}{(1+s)^n-1}\\
x &=& \frac{as}{1-(1+s)^{-n}}
\end{eqnarray}
$$
これで導出ができた。
(3)割引現在価値を使う方法
※こちらは導出と言うよりは、「そういう見方もあるんだな」という感覚で読むのが良いと思います。
投資で出てくる概念に、割引現在価値というものがある。
元金a, 月利s, 複利で毎月元利均等返済していくとする。 (利息から返している限り、単利でも複利でも同じ結果になる)
aを借りてから、仮にそのまま返済しなかったとしたら、
- 1ヶ月後aの価値は利息を含めて $a_1 = a(1+s)$ になる。
- 2ヶ月後aの価値は利息を含めて $a_2 = a(1+s)^2$ になる。
- ...
- nヶ月後aの価値は利息を含めて $a_n = a(1+s)^n$ になる。
これらから逆算してaを求めたものを割引現在価値と呼ぶ。1ヶ月後のa_1は、aと等しいとみなす。
ローンとは、 借りる金額 = 返済それぞれの割引現在価値の合計 となる概念である。
毎月xずつ返済していくとすると、
- 1ヶ月目の返済xは、現在価格aのうちの$x/(1+s)$に対応する。
- 2ヶ月目の返済xは、現在価格aのうちの$x/(1+s)^2$に対応する。
n回払いでaすべてを完済するとしたら、aは以下のように表すことができる。
$$
a = \frac{x}{1+s} + \frac{x}{(1+s)^2} + \frac{x}{(1+s)^3} + ... + \frac{x}{(1+s)^n}
$$
これは、等比数列の和の形式になっている。
初項は$x/(1+s)$で、公比は$1/(1+s)$
等比数列の和は公式があって、初項A,公比rの等比数列の和S_nは以下の形式で表せることがわかっている。
$$
S_n = \frac{A(1-r^n)}{1-r}
$$
それぞれ代入して変形していくと
$$
\begin{eqnarray}
a &=& \frac{\frac{x}{1+s}(1-(\frac{1}{1+s})^n)}{1-\frac{1}{1+s}}\\
a &=& \frac{x(1-(1+s)^{-n})}{(1+s)-1}\\
a &=& \frac{x(1-(1+s)^{-n})}{s}\\
x &=& \frac{as}{1-(1+s)^{-n}}
\end{eqnarray}
$$
ローンの公式が導き出せた。
まとめ
本記事ではローンの公式の導出過程をまとめました。
利息の性質は他にも色々あって、このローンの公式を起点に他にも公式を導き出せます。
公式を作ると、利息というものの特性がよく見えるようになります。こちらはまた別の記事にまとめようと思います。