はじめに
- Part1(基礎編)(ここ)
- Part2(円柱編)
- Part3(角柱編)
- Part4(SDFの加工編)
こんにちは、アドベントカレンダー9日目の避雷です。レイマーチングをするにあたって必要不可欠な関数に「距離関数」というものがあります。コピペや暗記してしまえば何も考えずに使えるこれらの関数ですが、ちゃんと考察してみると面白い気づきがあったりします。
今回はレイマーチングにおいて描画処理の根幹を担う距離関数について数学的な解釈をしたいと思います。
本編
そもそもSDFとは
SDFとはSignedDistanceFunction(符号付距離関数)の略で、一般に以下の形で定義される関数です。
f:R^n \rightarrow R (nは通常2,3) \\
f(r) < 0 (rが物体内面にあるとき) \\
f(r) > 0 (rが物体外面にあるとき) \\
|f(r)| = 物体表面からの距離
要するにある点Pと描画対象の物体との距離を取り、内側なら-1 外側なら 1 をかけるって感じの関数です。内側・外側の概念がある以上取り扱えるのは閉曲面だけな気もしてきますが、そこらへんは上手く誤魔化すことができます。
定義だけ見てもイマイチピンとこないと思うので、実際の関数を見てみましょう。
球
球の描画は以下の関数で行われます。
float map(vec3 p,vec3 origin,float radius){
return length(p - origin) - radius;
}
「距離」の定義によっては同等な式でも全く違う図形が出力されます。glslのlengthでは距離を以下のように定義しています。
d(a,b) = \sqrt{(a_1 - b_1)^2 + (a_2 - b_2)^2 + (a_3 - b_3)^2}
コレとは別に自前でlength_2みたいなものを定義してあげると、例えばManhattan距離での実装ができたりします。
d(a,b) = |a_1 - b_1| + |a_2 - b_2| + |a_3 - b_3|
新しく作る「距離」はある程度滅茶苦茶でも良いのですが、描画結果が納得いくものであるためには距離の公理を満たしていると良いと思います。集合位相論的な「距離」についてはここでは詳しく扱いません。
AND|OR演算について
レイマーチングでは 引数の最大値を返すmax,引数の最小値を返すminを使って複数の立体の合成、くり抜き、共通部分のみ抽出、という操作をすることができます。
直方体
よく使われる直方体のSDFはこんな感じです。
float map(vec3 p,float size){
return max(abs(p) - size / 2.);
}
これは実は近似的な関数です。下のような例を見れば、このSDFは厳密には誤りであると言えます。
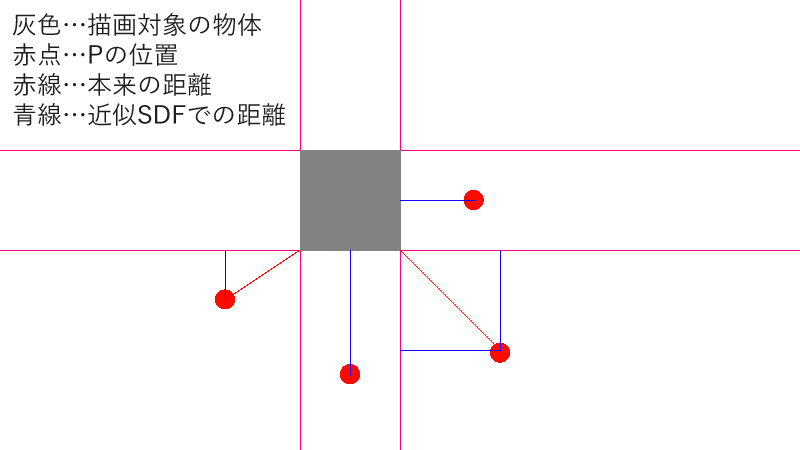
どうですか?結構雑じゃない? この近似がなぜ許されているかと言うと、近似との誤差が出る部分は全部最短距離が辺の上に乗るため実質描画されないからです。
この関数の別の解釈としては、先述のAND|OR演算を利用して、3枚の壁の共通部分のくり抜き、とすることもできます。
法線取得
レイマーチングについて、物体表面の法線ベクトルの取得は以下の関数getNormalで行われます。
const float EPS = 0.001;
vec3 getNormal(vec3 p) {
return normalize(vec3(
map(p + vec3(EPS, 0.0, 0.0)) - map(p + vec3(-EPS, 0.0, 0.0)),
map(p + vec3(0.0, EPS, 0.0)) - map(p + vec3( 0.0, -EPS, 0.0)),
map(p + vec3(0.0, 0.0, EPS)) - map(p + vec3( 0.0, 0.0, -EPS))
));
}
この関数で行っていることはシンプルで、x,y,z成分での偏微分を求め、その値をx,y,z成分に持つベクトルを生成しています。ベクトル解析を齧ったことがある人ならGradientを算出している、と表現するとわかりやすいと思います。
おわりに
ざっくり基礎的な部分について書いてみました。次回はもうちょっと複雑な図形についても解説が出来たらよいなと思います。